基于三链DNA结构的全错位排列问题算法
2012-11-13殷志祥赵前进
孙 侠,殷志祥,赵前进,许 峰
(安徽理工大学 理学院,安徽 淮南 232001)
基于三链DNA结构的全错位排列问题算法
孙 侠,殷志祥,赵前进,许 峰
(安徽理工大学 理学院,安徽 淮南 232001)
目前,一种新型的DNA计算模型——三链DNA计算模式正越来越受到人们的关注。已经证实,DNA单链能在RecA蛋白的介导下与同源的双链DNA匹配成稳定的三链DNA结构,利用此三链核酸提取目的DNA序列是完全可行的。文章提出了全错位排列问题的基于三链DNA的计算模型,由于表示可能解的链都是双链,彼此不会错配,也不会形成发夹结构,这样就大大降低了编码复杂度和计算错误率。
三链DNA结构;抗原中介;全错位排列问题
DNA计算是一种以DNA和相关的某些生物酶作为最基本材料的,基于某种生化反应原理的新型分子生物计算方法。自1994年,美国加利福尼亚大学的Adleman[1]博士提出DNA计算的思想以来,DNA计算领域的研究有了长足的发展。许多NP—完全问题和困难计算问题都得到了解决,如中国邮递员问题,图的着色问题,匹配问题,图的最大团问题,最小覆盖问题,0-1规划问题等[2-6]。以前的DNA计算方法都是基于Watson-Crick原则,利用碱基间的互补配对来完成基本的运算。随着实验的技术的不断提高,近年来许多研究者在实验中相继证实分子可以以其它结构存在,比如三链状结构。至今已发现的三链结构有三股螺旋结构和三股发辫结构。对三链DNA的研究主要是医学方面,也有人尝试用三链DNA解决有关问题,方刚等[7]用三链DNA计算模型解决了3-SAT问题、三顶点着色问题,杨静等[8]利用三链DNA计算模型解决了0-1整数规划问题。
全错位排列问题是组合数学中常见的一类问题,作者给出过它的基于芯片、基于表面的DNA计算模型[9,10],这里将尝试给出基于三链DNA的计算模型,与前面两种模型相比,利用三链结构,降低了编码的复杂度,而且反应后得到的解以双链的形式出现,对于解的正确率有很好的效果。
1 三链DNA的结构与功能[11]
1957年,Feisenfeld[12]等首次提出了三链核酸(triple-helix DNA/triplex)的概念。三螺旋结构是在双螺旋结构的基础上形成的。三链DNA是由经典的Watson-Crick双螺旋中含有多聚嘌呤的那条链通过Hoogsteen和反式Hoogsteen型氢键与第三条链相作用形成的。第三条链位于Watson-Crick双链的大沟中,靠Hoogsteen碱基对的氢键相联系。见图1所示。
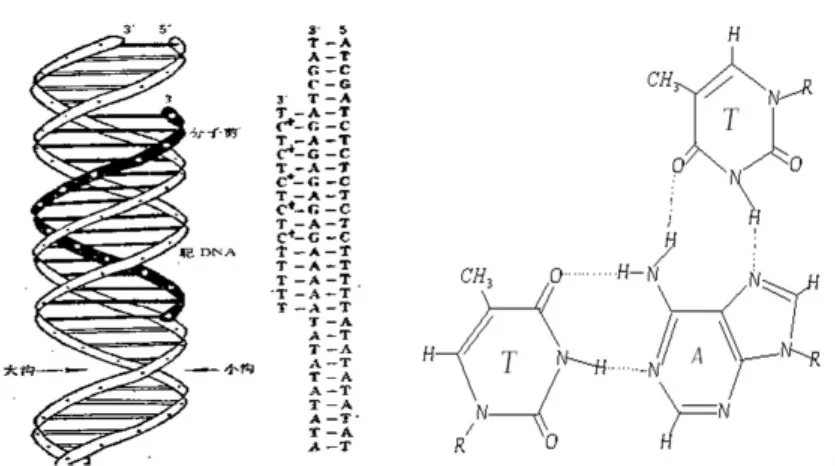
图1 三螺旋DNA链的空间结构与分子结构
2004年Shigemori等发现DNA在RecA蛋白及ATPr S的存在下,与线性双螺旋DNA可形成稳定的三链结构(见图2)。经证实由RecA蛋白介导形成的三链DNA是相当稳定的[13]。2009年方刚[7]通过实验证实使用 RecA蛋白介导的三链核酸提取目的DNA序列的方法是完全可行的,它可以被设计用来进行相应的分子运算。目前关于三链DNA的研究偏重于它的医学应用,如通过三螺旋结构的形成,寡聚核苷酸可以充当切割DNA的“分子剪刀”和提供抑制基因转录的新手段等等。下面给出全错位排列问题的基于三链DNA结构的计算模型。
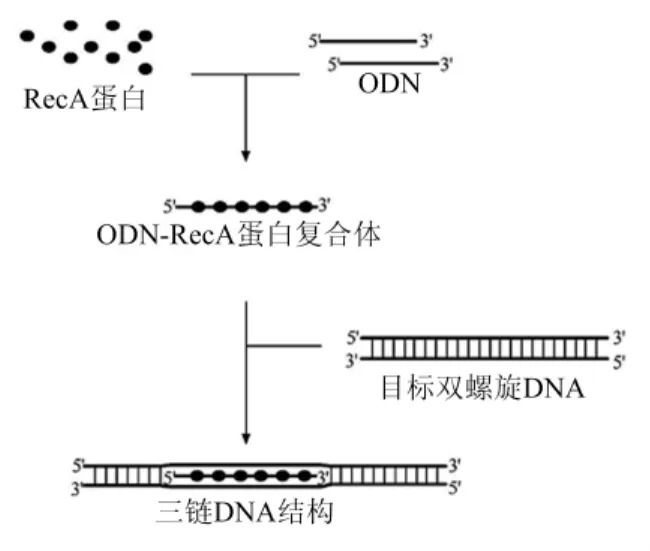
图2 RecA蛋白介导下三链DNA形成模式图
2 全错位排列问题的三链DNA计算模型
集合{1,2,…,n}的一个全错位排列是该集合的一个满足条件ij≠j(1≤j≤n)的全排列i1i2…in,即集合{1,2,…,n}的一个没有一个数字在它的自然顺序位置上的全排列,集合{1,2,…,n}的全错位排列问题即是要求出该集合的所有全错位排列。
下面以3元集合{1,2,3}的全错位排列问题为例,要求出集合{1,2,3}的所有全错位排列就是要求出数字1,2,3都不在各自的自然位置上的全排列。经过仔细分析,容易发现问题存在3个原子命题:① 数字1排在第二个位置上,记为x;② 数字2排在第一个位置上,记为y;③ 数字3排在第一个位置上,记为z。它们的否命题分别为:¯x,¯y,¯z。问题要求满足条件:(1)若数字1在第二个位置上,则数字3不在第二个位置;(2)若数字2在第一个位置上,则数字3不在第一个位置;(3)若数字1在第三个位置上,则数字2不在第三个位置。上述问题可以转化为下面的命题公式:F=(¯x∨z)∧(¯y∨¯z)∧(x∨y)的满足性问题。
2.1 编码
公式F中含有3个变元3个子式,首先我们构造两组寡聚核苷酸片段,分别表示x,y,z和¯x,¯y,¯z,比如x对应的DNA链表示x取值为1,¯x对应的DNA链表示x取值为0,其它变量同样。由于使用较长探针能更有效地提取目的序列,所以每个变量均用完全不同的30bp的DNA表示,见图3所示。公式F总共有23=8个可能解,那么每一个解就由一条90bp的双链DNA表示,而这些双链DNA的模版链序列由那些表示每个变量取值的DNA序列串联而组成。在此这些表示每个变量取值的DNA均作为探针来提取解。
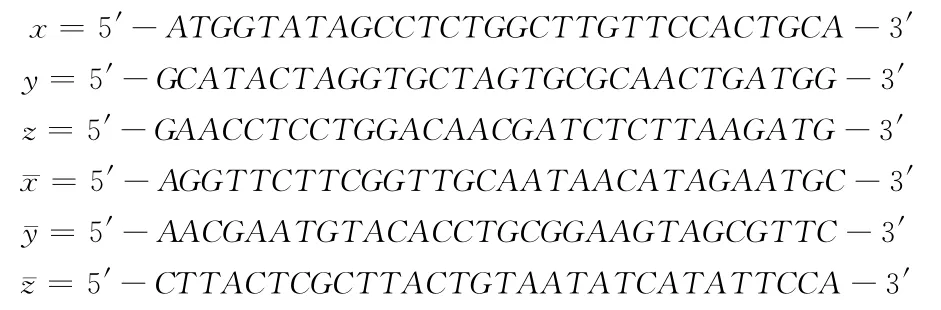
图3 编码示意图
2.2 生物操作
下面介绍相应的生物操作。
Step0将编码后的DNA片段放入DNA自动合成仪,合成F的全部解空间序列[14],然后用PCR扩增成双链DNA,它们构成初始数据池tube0;将表示每个变量取值的DNA单链 的5′端以SS-Biotin标记,作为探针使用,这里用SS-Biotin标记的作用是增大结合空间,便于磁珠吸附。
Step1为了得到满足第一个子式(¯x∨z)的解,我们分三步进行:
(1)在表示x=0,z=1的DNA单链的5′端添加一个RecA蛋白,再标记上生物素。使这些DNA单链和抗原蛋白质在含有ATPγS溶液混合在适宜条件下生成RecA蛋白-DNA复合体,把这些核蛋白细状体的DNA链作为模板构造探针,探针见图4。
(2)将上述探针混合到数据池tube0中,探针在RecA蛋白介导下,将与满足第一子式的解形成稳定的三链结构。
(3)将上步得到的三链DNA与表面涂有链亲和素的磁珠混合,由于链亲和素的高度亲和力,三链DNA与探针一起被吸附在磁珠上,不满足该子式的双链DNA被分离出去。对三链DNA经过洗脱及脱蛋白处理,第三条链从三链中分离出来,得到满足第一个子式的双链DNA。将这些双链DNA装入试管tube1。
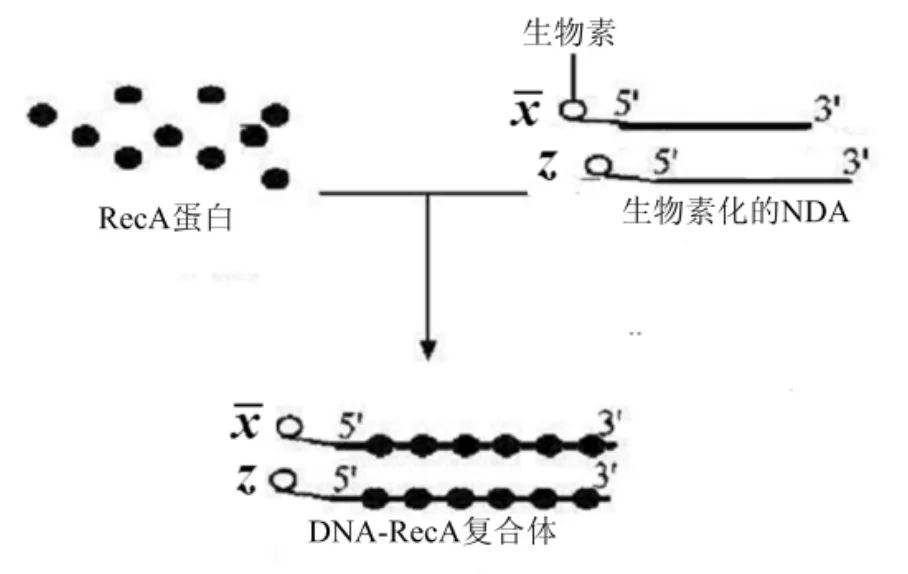
图4 RecA包裹的探针¯x和z
Step2为了得到满足第二个子式(¯y∨¯z)的解,同 Step1类似,我们分三步进行:
(1)将表示y=0,z=0的DNA单链与RecA蛋白,ATPγS溶液混合,在适宜条件下生成核蛋白细状体,把这些核蛋白细状体的DNA链作为模板构造探针。
(2)将上述探针混合到数据池tube1中,探针在RecA蛋白介导下,将与满足第二子式的解形成稳定的三链DNA。
(3)利用磁珠分离技术,剔除不满足该子式的双链DNA,保留满足条件的三链DNA。再对三链DNA经过洗脱及脱蛋白处理,第三条链从三链中分离出来,得到满足该子式的双链DNA。将这些双链DNA装入试管tube2。
Step3为了得到满足第三个子式(x∨y)的解,同样分三步进行:
(1)将代表x=1,y=1的DNA单链与RecA蛋白,ATPγS溶液混合,在适宜条件下生成核蛋白细状体,把这些核蛋白细状体的DNA链作为模板构造探针。
(2)将上述探针混合到数据池tube2中,探针在RecA蛋白介导下,将与满足第三子式的解形成稳定的三链结构。
(3)利用磁珠分离技术,剔除不满足该子式的双链DNA,保留满足条件的三链DNA。再对三链DNA经过洗脱及脱蛋白处理,第三条链从三链中分离出来,得到满足该子式的双链DNA。将这些双链DNA装入试管tube3。
Step4对tube3中的DNA进行PCR扩增和纯化,即可读出问题的解。
本问题的解是101,010,对应得到三元集合{1,2,3}的全错位排列有231和312。
2.3 模型分析
全错位排列问题是组合数学中的一类重要问题,文章利用DNA单链能在RecA蛋白的介导下与同源的双链DNA匹配成稳定的三链DNA这一性质,提出了基于三链DNA的计算模型,与以往的模型相比,由于表示可能解的链都是双链,彼此不会错配,也不会形成发夹结构,表示探针的单链由于和RecA蛋白结合,也不会出现上面的错误,这样就大大降低了编码复杂度和计算错误率,同时可以进行大规模的分子计算。
[1]Adleman L.Molecular computation of solution to combinatorial problems[J].Science,1994,66(11):1021-1024.
[2]许 进,张 雷.DNA计算原理、进展及难点(1):生物计算系统及其在图论中的应用[J].计算机学报,2003,26(1):1-11.
[3]高 琳,许 进.图的顶点着色问题的DNA算法[J].电子学报,2003,4:494-497.
[4]殷志祥,张风月,许 进.0-1规划问题的DNA计算[J].电子与信息学报,2003,25(1):62-66.
[5]殷志祥,张风月,许 进.基于分子信标的DNA计算[J].生物数学学报,2003,18(4):1-5.
[6]殷志祥.图与组合优化中的DNA计算[J].科学出版社,2004.12:16-23.
[7]方 刚,张社民,朱 岩,等.基于三链核酸的DNA计算[J].生物信息学,2009,7(3):181-185.
[8]杨 静,殷志祥.基于抗原中介三链DNA结构的0-1整数线性规划[J].计算机工程与应用,2008,44(2):76-79.
[9]孙 侠,殷志祥,张家秀.全错位排列问题的基于表面的DNA计算模型[J].生物数学学报,2009,24(3):513-517.
[10]孙 侠,殷志祥,李 勇,等.全错位排列问题的基于芯片的DNA计算模型[J].大学数学,2010,26(2):79-82.
[11]白宝璋,霍玉芹,刘福春,等.三链DNA的结构与功能[J].农业与技术,1996,92(3):27-28.
[12]Huamin JI,Ioydm S,Richard A G.Rapid isolation of cosmid insert DNA by triple-helix-mediated affinity capture[J].Genetic Analy-sis Tech Application,1994,112(2):43-47.
[13]Rao B J,Dutreix M,Radding C M.Stable three-stranded DNA made by RecA protein[J].Pro Natl Acad Sci USA,1991,88(8):2984-2988.
[14]Braich R S,Chelyapov N,Johnson C,et al.Solution of a 20-variable 3-SAT problem on a DNA computer[J].Science,2002,296(4):499-502.
DNA Computing Model on Triple-stranded of the Whole Error Permutation Problems
Sun Xia, Yin Zhixiang, Zhao Qianjin, Xu Feng
Now people closely pay attention to a new DNA computing mode based on triple-stranded DNA.It is proved that single-strand DNA can match with homologous double-stranded into a stable three-stranded structure mediated by RecA protein and the extraction of the target DNA is feasible by the three-stranded DNA.The paper gives the DNA computing model on triple-stranded.Because feasible values are coded by double-stranded DNA,wrong hybridization does not take place and hairpin structure does not form.Thus in this way,encoding complexity and the errors in computation will be decreased.
triple-stranded DNA;Antigen intermediary;the whole error permutation problem
Q812
A
1673-1794(2012)02-0018-03
孙 侠(1980-),女,安徽凤台人,讲师,硕士,研究方向:图论,给合优化及DNA计算。
国家自然科学基金(60873144,61170172,61073102,60973050),安徽省优秀青年基金(06042088),安徽省教育厅自然科学基金项目(KJ2009B071Z,KJ2009B174Z),安徽省高等学校省级优秀青年人才基金(2009SQRZ059,2011SQRL035)
2012-01-15
