深埋隧洞开挖岩爆数值模拟与预测
2012-11-12陈文亮刘仲秋
陈文亮,章 青,刘仲秋
(1.浙江省水利河口研究院,杭州 310020;2.河海大学工程力学系,南京 210098;3.山东农业大学,山东 泰安 271000)
1 研究背景
岩爆是高应力区进行地下开挖时,由于破坏了岩体的力学平衡,围岩中产生了应力集中而使岩体产生脆性破坏并伴随能量释放的动力失稳现象。有关统计资料表明[1],岩爆多发生在强度高、厚度大的坚硬岩(煤)层中,一般而言,随着埋深的增加岩爆发生的机会将越来越大,所以在深层开挖中研究岩爆显得尤为重要。
近几十年来,国内外采矿界和岩体工程界的专家、学者对岩爆机理、岩爆预测以及岩爆防治诸方面进行了大量的研究,取得了一定成果[2-6]。在岩爆机理方面除了传统的强度理论、刚度理论、岩爆倾向理论等外,近年来谢和平[7]采用分形理论,潘岳等[8]采用突变理论,陈卫忠[9]、王耀辉[10]、秦剑峰、卓家寿[11]等采用能量理论来解释岩爆现象。在岩爆预测方法方面根据不同的岩爆机理理论,可得出不同的判据,主要分为应力判据,岩性判据,能量判据,临界深度判据等。但由于岩爆是极为复杂的动力失稳现象,岩爆的机理到目前为止还不很清楚,利用传统的岩爆分析方法来预测岩爆遇到了极大的困难,在这种情况下,人工智能、专家系统、神经网络在岩爆预测中得到了很好的运用,如冯夏庭等[12]提出的基于支持向量机的预测方法为岩爆预测提供了一条十分有效的途径。
在岩爆的数值模拟方面,普遍的做法是根据对围岩二次应力场的模拟,采用不同的判据预测方法预测岩爆是否发生,其中采用的岩石本构关系基本是弹性本构或者弹塑性本构。近年来,越来越多的研究表明深埋隧洞岩爆具有典型的脆性破坏特征[13-14],因此采用传统的弹塑性本构来模拟岩爆的脆性破坏问题并不合适。
本文提出在深埋隧洞岩爆数值模拟中采用符合深埋隧洞岩爆岩体脆性破坏特征的复合破坏准则弹脆塑性本构模型,并利用ABAQUS的二次开发功能编制了此弹脆塑性本构的UMAT程序并将其用于岩爆的数值模拟。结合锦屏二级水电站辅助洞工程,通过三维有限元数值模拟,综合运用各种判据和方法建立岩爆的预测体系,对岩爆发生情况和部位进行了预测,对岩爆的预测具有一定的参考价值。
2 数值分析模型
2.1 计算采用的本构模型与破坏准则
岩爆破坏是典型的脆性破坏,其破坏方式主要由拉张破坏、剪切破坏和拉剪复合破坏。以往的研究大多采用理想弹塑性本构关系,并且对屈服破坏的判断采用单一的屈服准则,如Mohr-Coulomb准则和Drucker-Prager准则。这些破坏准则只能反映岩石压剪破坏而不能很好的反映岩石的脆断破坏,且理想弹塑性本构关系也不能反映岩石的脆性破坏特征。为了能够模拟岩爆的脆性破坏,本文考虑把反映脆性破裂准则的最大拉应力准则(Rankine准则)和弹脆塑性本构联合,弹脆塑性本构中的屈服准则采用Drucker-Prager准则。Rankine准则结合Drucker-Prager准则弹脆塑性本构是综合考虑受拉和受压2种破坏模式的复合准则。通过这个复合准则,材料的脆性破坏可被分为拉伸破坏和压剪破坏2种形式,拉伸形式的断裂破坏由Rankine准则判断,剪切形式的脆塑性破坏由Drucker-Prager准则判断。
Rankine准则可表达为

又Drucker-Prager屈服准则为

式中:I1,J2分别为应力张量的第一不变量和应力偏量的第二不变量;θ为Lode角;α,k均为与材料的黏聚力c和内摩擦角φ有关的参数;f't为材料拉伸强度。联立2式得

令
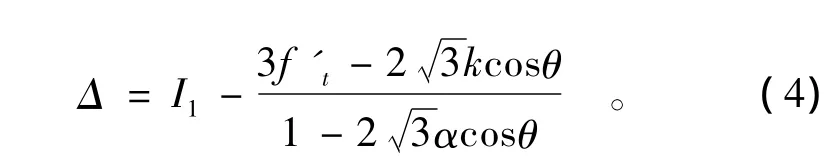
当Δ≥0时采用Rankine破坏准则,岩体发生脆性拉断破坏;当Δ<0时采用Drucker-Prager屈服准则,岩体发生剪切形式的脆性破坏,按脆塑性本构理论进行求解。关于脆塑性模型理论分析与数值实现方法,文献[15-16]进行了详细的阐述,在此不再赘述。
由于目前商业软件中没有弹脆塑性本构关系也没有这样的脆性岩石复合破坏准则,因此作者利用ABAQUS的二次开发功能编制了此弹脆塑性本构的UMAT程序,用于高地应力条件下硬岩的岩爆问题的数值模拟。
2.2 计算模型及参数
三维数值分析模型根据锦屏二级水电站辅助洞隧洞的结构特征和工程地质条件建立,选用岩爆高发的Ⅱ类围岩建立计算模型,隧洞的断面形状为“直墙 +半圆形”,断面大小为5.5 m×5.7 m,选取的计算区域为30 m×30 m×27 m,如图1所示。洞室开挖采用全断面一次开挖。计算模型在顶面作为应力边界,施加由拟合求得的竖直地应力为49MPa,其它边界施加法向位移约束条件,垂直隧洞轴线和沿隧洞轴线的水平地应力通过侧压力系数k1和k2施加,分别为0.8和0.9。计算中采用二次开发的基于Rankine准则和Drucker-Prager准则的岩石弹脆塑性本构关系。计算中材料参数见表1。
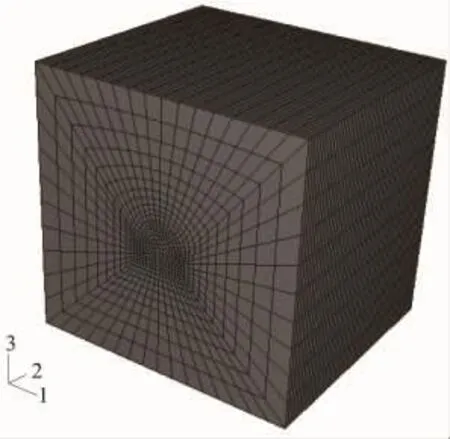
图1 模型示意图Fig.1 Diagram of the model

表1 材料参数Table 1 Parameters of the material
3 数值分析结果及岩爆预测
3.1 规范判据法的岩爆预测
根据水力发电工程地质勘察规范(GB50287—2006),利用围岩强度应力比Rb/σm(σm为最大主应力)的大小进行岩爆等级的判别,考虑了岩体初始应力场和岩石的性质。虽然岩爆的发生是由洞室开挖的应力重分布引起,但应力重分布的基础是岩体的初始应力。因此,用围岩的初始最大主应力也可反映洞室开挖后应力重分布的相对大小。利用围岩强度应力比Rb/σm的大小进行岩爆等级的判别既可与岩体应力的分类配套,又便于操作。

图2 初始最大(绝对值)主应力分布Fig.2 Distribution of initial maximum principal stress
根据初始地应力场的数值模拟,得考虑洞段处的最大主应力分布如图2所示,结合此洞段处岩石的饱和单轴抗压强度指标,可得到此洞段的强度应力比值大约为1.8,根据规范判据法此洞段会发生强烈岩爆(Ⅲ级)。
3.2 基于应力强度比判据的岩爆预测
国内外学者多将有限元计算断面洞壁切向应力σθ和岩石单轴抗压强度Rb之比值作为岩爆判据,称之为应力强度比判据。研究结果表明:无岩爆活动洞段 σθ/Rb<0.3;轻微岩爆活动段σθ/Rb介于0.3~0.5之间;中等岩爆洞段σθ/Rb介于0.5~0.7之间;发生强烈岩爆活动时,σθ/Rb比值至少大于0.7。应力强度理论是岩爆机制静力学解释的两大理论之一,在此理论基础上建立的应力强度比岩爆预测判据在国内外得到广泛的应用,国内的天生桥及二郎山隧洞利用此理论成功地对岩爆进行了预测。
图3为切向应力σθ分布。由图3知σθ在角点处和洞肩处比较大,分别为174.0MPa和110.6MPa,而岩石单轴抗压强度Rb为90MPa,则在角点处σθ/Rb=1.9,在洞肩处σθ/Rb=1.2,根据应力强度比判据此2处有可能发生强烈岩爆。
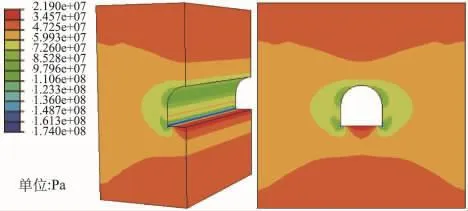
图3 切向应力分布Fig.3 Distribution of tangential stress
3.3 基于主应力变化的岩爆预测
为了分析隧洞断面上离洞壁不同距离处主应力变化,在洞顶,洞肩和角点处分别取路径如图4所示,绘制主应力沿不同路径的变化图如5所示。

图4 路径分布Fig.4 Paths selected at the tunnel roof,shoulder and bottom corner points
隧洞开挖后主应力大小发生改变,主应力方向也发生旋转,最大主应力(最大主压应力)基本上为环向应力,与隧洞边界相切。在高地应力条件下,这会导致岩石破碎松动和剥落,甚至产生岩爆。大量研究表明,岩石松动剥落主要是脆性破坏引起的大量微裂隙造成的,而这些微裂隙主要沿着最大主压应力方向扩展,也就是沿着隧洞环向扩展。如果主应力方向在开挖过程中不断的旋转,而且其大小超过岩石开裂的槛值,那么新的微裂隙就会沿着新的最大主压应力方向开展,这样,岩石的微裂隙数量会不断增加,开展方向也会不断变化。因此,可以根据主应力的变化来预测岩爆的发生情况。
何思为等[17]提出一个 dσ3/(σ1-σ3)判别法,该判别法认为岩爆发生在洞室围岩dσ3/(σ1-σ3)正增长期增长很快的那一范围,dσ3/(σ1-σ3)越高,越容易引起岩爆。根据图5,列表计算 dσ3/(σ1-σ3)。根据表2中计算结果结合此判别法,在洞底角点处可能发生岩爆。

图5 不同路径上主应力变化Fig.5 Changes of principal stress in different paths

表2 不同路径dσ3/(σ1-σ3)值Table 2 Values of dσ3/(σ1-σ3)in different paths
3.4 基于可释放能量的岩体整体破坏准则的岩爆预测
谢和平[18]讨论了岩石变形破坏过程中能量耗散、能量释放与岩石强度和整体破坏的内在联系,提出了基于可释放能量的岩体整体破坏准则,分析了各种应力状态下岩石整体破坏的临界应力。外力对岩体所做的功一部分转化为介质内的耗散能Ud,使岩体强度逐步丧失;另一部分转化为逐步增加的可释放应变能Ue。当Ue储存并达到岩体单元某种表面能U0时,应变能Ue释放使岩体单元发生整体破坏。在主应力空间中,Ue难以沿最大压应力σ1方向释放,而易于沿最小压应力或拉应力σ3方向释放。受压情况下,岩体整体破坏准则为
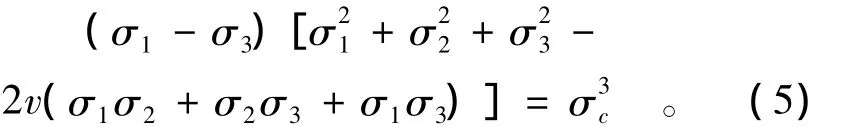
可以看出此准则为从能量角度分析得出的岩体整体破坏时主应力之间应满足的关系式,岩爆容易在主应力大小和方向发生改变的过程中发生,因此考虑引用基于可释放能量的岩体整体破坏准则来预测岩爆。把式(5)改写为
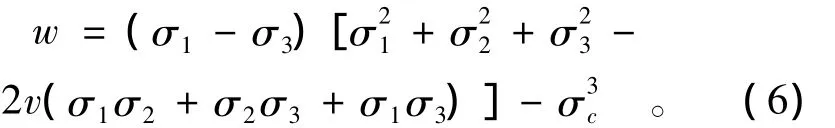
当w≥0时,围岩发生破坏,其中w=0时发生静态整体破坏,w>0时发生具有冲击能量的岩爆破坏。
根据此准则计算路径1-1,2-2和3-3上洞壁处的w值,如表3。从表中可以看出在3-3上洞壁上处的w值大于0,由此可以推测,在洞底角点处会发生岩爆。

表3 不同位置w的计算值Table 3 Calculated w values at different positions
4 结论
(1)为反映深埋隧洞开挖岩爆岩石的脆性破坏特征,提出在深埋隧洞开挖岩爆数值模拟中采用基于Rankine准则和Drucker-Prager准则的岩石弹脆塑性本构模型,并利用ABAQUS的二次开发功能编制了弹脆塑性本构的UMAT程序。
(2)由于岩爆机理的不确定性和预测方法的多样性,为了对岩爆发生地段和部位作出准确的判断,应综合运用各种经验判据和方法建立岩爆的预测体系。本文采用了4种不同的预测方法,除传统的应力强度比判据外,还把基于可释放能量的岩体整体破坏准则应用到岩爆预测中,对岩爆的预测具有一定的参考价值。
(3)根据规范判据法的预测结果,此洞段会发生强烈岩爆;对岩爆发生部位的预测上,4种方法都预测到了在洞室墙趾处将会发生岩爆,而规范判据法和应力强度比判据还预测在洞肩处也会发生岩爆。
(4)综合考虑上述4种预测方法,判定在墙趾和洞肩处发生岩爆可能性较大,这与锦屏二级水电站辅助洞岩爆实际发生情况基本一致。在岩爆烈度的预测上,规范判据法和应力强度比判据都高估了此隧洞岩爆发生的烈度,其他判据目前尚无岩爆烈度的对应关系,有待结合实际工程归纳总结。
[1]周宏伟,谢和平,左建平.深部高地应力下岩石力学行为研究进展[J].力学进展,2005,35(1):91-99.(ZHOU Hong-wei,XIE He-ping,ZUO Jian-ping.Developments in Researches on Mechanical Behaviors of Rocks under the Condition of High Ground Pressure in the Depths[J].Advances in Mechanics,2005,35(1):91-99.(in Chinese))
[2]徐则民,吴培关,王苏达,等.岩爆过程释放的能量分析[J].自然灾害学报,2003,12(3):104-109.(XU Ze-ming,WU Pei-guan,WANG Su-da,et al.Analysis of Energy Released in Process of Rock-burst[J].Journal of Natural Disasters,2003,12(3):104-109.(in Chinese))
[3]何满潮,苗金丽,李德建,等.深部花岗岩试样岩爆过程实验研究[J].岩石力学与工程学报,2007,26(5):865-876.(HE Man-chao,MIAO Jin-li,LI De-jian,et al.Experimental Study on Rockburst Processes of Granite Specimen at Great Depth[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(5):865-876.(in Chinese))
[4]WANG J A,PARK H D.Comprehensive Prediction of Rockburst Based on Analysis of Strain Energy in Rocks[J].Tunnelling and Underground Space Technology,2001,16(1):49-57.
[5]SHARAN SK.A Finite Element Perturbation Method for the Prediction of Rockburst[J].Computational Structures Technology,2007,85(17/18):1304-0309.
[6]VAHID H,KAISER P.Brittleness of Rock and Stability Assessment in Hard Rock Tunneling[J].Tunnelling and Underground Space Technology,2003,18:35-48.
[7]谢和平.岩爆的分形特征和机理[J].岩石力学与工程学报,1993,12(1):28-37.(XIE He-ping.Fractal Character and Mechanism of Rock Bursts[J].Chinese Journal of Rock Mechanics and Engineering,1993,12(1):28-37.(in Chinese))
[8]潘 岳,张 勇,于广明.圆形硐室岩爆机制及其突变理论分析[J].应用数学和力学,2006,27(6):741-749.(PANYue,ZHANGYong,YUGuang-ming.Mechanism and Catastrophe Theory Analysis of Circular Tunnel Rockburst[J].Applied Mathematics and Mechanics,2006,27(6):741-749.(in Chinese))
[9]陈卫忠,吕森鹏,郭小红,等.基于能量原理的卸围压试验与岩爆判据研究[J].岩石力学与工程学报,2009,28(8):1530-1540.(CHEN Wei-zhong,LV Senpeng,GUO Xiao-hong,et al.Research on Unloading Confining Pressure Tests and Rockburst Criterion Based on Energy Theory[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(8):1530-1540.(in Chinese))
[10]王耀辉,陈莉雯,沈 峰.岩爆破坏过程能量释放的数值模拟[J].岩土力学,2008,29(3):790-794.(WANG Yao-hui,CHEN Li-wen,SHEN Feng.Numerical Modeling of Energy Release in Rockburst[J].Rock and Soil Mechanics,2008,29(3):790-794.(in Chinese))
[11]秦剑峰,卓家寿.可储能原则在一类岩爆问题中的研究和应用[J].计算力学学报,2009,26(3):318-323.(QIN Jian-feng,ZHUO Jia-shou.Study on the Energy Storage Ability Criterion in a Kind of Rockburst and Application[J].Chinese Journal of Computational Mechanics,2009,26(3):318-323.(in Chinese))
[12]冯夏庭,赵洪波.岩爆预测的支持向量机[J].东北大学学报(自然科学版),2002,23(1):57-59.(FENG Xia-ting,ZHAO Hong-bo.Prediction of Rockburst Using Support Vector Machine[J].Journal of Northeastern University(Natural Science),2002,23(1):57-59.(in Chinese))
[13]READ R S.20 Years of Excavation Response Studies at AECL’s Underground Research Laboratory[J].International Journal of Rock Mechanics & Mining Sciences,2004,41:1251-1275.
[14]李育枢,李天斌,郑建国.西南某电站辅助隧洞岩爆地质力学模式研究[J].现代隧道技术,2009,46(1):41-46.(LI Yu-shu,LI Tian-bin,ZHENG Jian-guo.Study on the Geomechanical Patterns of Rockburst in the Access Tunnel of a Hydroelectric Power Station in Southwest China[J].Modern Tunnelling Technology,2009,46(1):41-46.(in Chinese))
[15]沈新普,岑章志,徐秉业.弹脆塑性软化本构理论的特点及其数值计算[J].清华大学学报,1995,35(2):22-27.(SHEN Xin-pu,CEN Zhang-zhi,XU Bing-ye.Characteristics and Numerical Implementation of Elastic-Brittle-Plastic Constitutive Model[J].Journal of Tsinghua University,1995,35(2):22-27.(in Chinese))
[16]郑 宏,葛修润,李焯芬.脆塑性岩体的分析原理及其应用[J].岩石力学与工程学报,1997,16(1):8-21.(ZHENG Hong,GE Xiu-run,LEE CF.Analytical Principle for Rock Mass with Brittle-Plasticity and Its Applications[J].Chinese Journal of Rock Mechanics and Engineering,1997,16(1):8-21.(in Chinese))
[17]何思为,卢世杰,向贤礼.拱形洞室围岩内岩爆的计算机模拟与控制方法[J].探矿工程,2002,(4):55-57.(HE Si-wei,LU Shi-jie,XIANG Xian-li.Computer Modeling and Controllable Options for Strain Rock Burst at Arched Drift[J].Exploration Engineering,2002,(4):55-57.(in Chinese))
[18]谢和平,鞠 杨,黎立云.基于能量耗散与释放原理的岩石强度与整体破坏准则[J].岩石力学与工程学报,2005,24(17):3003-3010.(XIE He-ping,JU Yang,LI Li-yun.Criteria for Strength and Structural Failure of Rocks Based on Energy Dissipation and Energy Release Principles[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(17):3003-3010.(in Chinese))
