Cole方程单边界层的渐近解探讨

卢西庄 (亳州师范高等专科学校理化系，安徽 亳州 236800)

Cole方程单边界层的渐近解探讨

卢西庄 (亳州师范高等专科学校理化系，安徽 亳州 236800)

利用边界层函数法构造了Cole方程单边界层的渐近解。证明了解的存在唯一性,同时给出了关于小参数ε的n-阶的余项估计。

Cole方程; 奇摄动; 渐近解; 边界层函数法

Cole方程在不同条件下产生多种奇摄动现象,引起一些学者的兴趣。文献[1-3]对其中的某些情况做出一些研究,采用了不同的方法。下面，笔者利用边界层函数法对单边界层情况进行探讨。

对于Cole方程：

假设Agt;B-1,Bgt;1。式 (1)可变为：

1 构造形式渐近解

设问题(3)的形式渐近解为：

(5)

(6)

Πx(τ)=Π0x(τ)+εΠ1x(τ)+ε2Π2x(τ)+…

(7)

其中x=(y,z)T,τ=t/ε。为叙述方便,令：

将式(5)～(7)代入式(3), 按2种尺度t、τ分开,并展成ε的幂级数,比较ε的同次幂系数,可得：

(8)

(9)

(10)

(11)

(12)

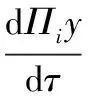
(13)

(14)

(15)

笔者解决问题的方法是将边值问题(3)转化为初值问题加以解决。设：

x(0,ε)=x0+εx1+ε2x2+…xi(i=0,1,2,…)

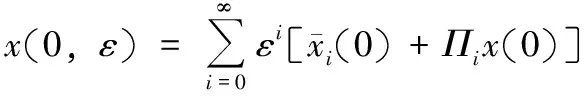
(16)

1.1形式渐近解的零次近似

1.2形式渐近解的一次及n次近似

由式(9)和式(11)得：

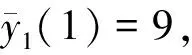
与一次项的求法完全类似,利用式(9)、式(11)、式(13)、式(15)及相关定解条件,可逐步求出2次、3次直到n次的渐近解各项及xi(i=2,3,…,n)。所解方程都是一次方程,其中边界项都随τ→+∞指数式地趋于0。

2 主要结论

笔者研究的问题满足以下条件:

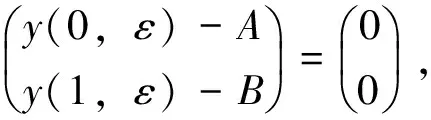
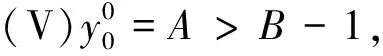
令：

根据文献[4]定理4.1 可得：

定理1存在常数ε0,δgt;0和cgt;0使得当0lt;ε≤ε0时,在曲线L0=L01∪L02的δ邻域中,存在问题(2～4)的唯一解x(t,ε),且对0≤t≤1满足不等式：

‖x(t,ε(-xn(t,ε)‖≤cεn+1

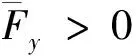
[1]Nayfeh A H. Introduction to Perturbed Techniques[M]. New York: John Wiley amp; Sons,1981.

[2]Robert L,Michel G. Nonstandard analysis: a practical guide with applications[M]. New York:Springer,1981.

[3]王爱峰.用微分不等式解Cole问题[J].淮阴师范学院学报(自然科学版),2006,5(1):1-3.

[4]瓦西里耶娃 A B,布图索夫 В Ф.奇异摄动方程解的渐近展开[M].北京:高等教育出版社,2008.

[编辑] 洪云飞

10.3969/j.issn.1673-1409(N).2012.04.002

O175.14

A

1673-1409(2012)04-N004-03

2012-01-26

安徽省教育厅自然科学研究项目(KJ2010B124);亳州师专数学教育省级特色专业建设点资助项目。

卢西庄(1966-)，男，1989年大学毕业， 硕士,讲师,现主要从事微分方程的奇摄动理论方面的教学与研究工作。