考虑谐振的混合型有源滤波器参数优化配置

夏向阳， 徐林菊， 刘飞龙

(1.长沙理工大学电气与信息工程学院， 长沙 410004； 2.大唐公司耒阳发电厂， 耒阳 421856)

考虑谐振的混合型有源滤波器参数优化配置

夏向阳1， 徐林菊1， 刘飞龙2

(1.长沙理工大学电气与信息工程学院， 长沙 410004； 2.大唐公司耒阳发电厂， 耒阳 421856)

针对混合型有源滤波器在实际应用时，无功补偿不能出现过补偿及谐振的问题，提出采用电容无功补偿功率与串并联谐振频率的关系作为约束条件对并联混合型有源滤波器SHAPF(shunt hybrid active power filter)参数进行优化配置。寻优算法采用改进的粒子群优化算法IPSO(improved particle swarm optimization)，根据粒子群算法参数速度v和惯性因子w的关系，提出时变的非线性三角函数方法来控制参数，加速了算法的收敛速度，防止陷入局部最优。通过Matlab进行仿真验证，SHAPF的参数设计得到了优化配置，具有良好的滤波效果。在实例应用中，有效地避免了谐振，具有一定的工程应用价值。

电容器容量； 串并联谐振频率； 无功过补偿； 时变非线性三角函数； 参数的优化配置

混合型有源滤波器性能比高，更利于工程的实现，日益成为高压大容量系统进行谐波抑制和无功补偿的首要措施[1]，但容易受到背景谐波电压的影响。这些谐波电压可能导致系统谐振和直流侧电压升高[2，3]，损坏混合型有源滤波器的逆变开关和直流侧电容。

针对上述问题，文献[2]通过多目标遗传算法对混合有源滤波器有源部分注入支路的参数进行优化，采用并联多个逆变器和直流侧电容的多重化主电路形式、先进的控制算法来减小基波谐振支路的谐波分压，显然混合有源滤波器的设计经费很大。文献[4，5]通过建立电气模型、结构以及最优的控制策略设计有源电力滤波器有源和无源部分的参数设计，确保了混合型有源滤波器的安全有效运行，但没有对参数进行优化性设计。而文献[6]采用改进粒子群优化算法对混合滤波装置中无源滤波器进行多目标优化设计，但没有考虑谐振问题。

鉴于以上文献的不足，本文针对混合型有源滤波器在实际应用中，混合有源滤波器无源部分PPF(passive power filter)与系统发生串并联谐振以及无功过补偿引起谐振对有源部分APF(active power filter)中IGBT元件损害的问题，采用电容无功补偿功率与串并联谐振频率的关系作为约束条件，改进的粒子群算法对并联混合型有源滤波器SHAPF参数进行优化配置，达到经济费用低、避免谐振、滤波效果好的目的。

1 优化问题的数学模型

混合型有源滤波器，兼顾了无源滤波器和有源滤波器长处，减少谐波补偿系统的投资、性能比高，满足高压大容量系统实用化的要求，达到实用化谐波抑制的目的[7]。SHAPF优化的问题是在SHAPF拓扑结构和控制目标确定的前提下，寻求其优化配置参数，SHAPF拓扑结构如图1所示。

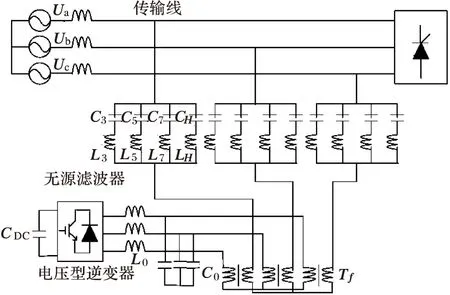
图1 SHAPF拓扑结构图

SHAPF由APF与PPF串联混合而成[1，7，8]，由有源和无源部分共同抑制谐波，APF主要由隔离变压器、输出滤波器、电压型逆变器组成。其中PPF采用多个调谐滤波器组成，其调谐频率根据被补偿对象的谐波确定，降低了APF的容量和电压等级，为谐波电流提供低阻抗通路[1]。

1.1 优化问题描述

实用滤波器的参数优化问题能够在最低费用下满足谐波抑制的要求。

(1)SHAPF无源部分主要由电感L和电容C组成，其经济性主要由元件的功率容量决定[9～12]。本文采用的优化配置的目标函数为

minf=fP(QP)+fA(S)

(1)

式中：minf表示最小的经济费用；fP(QP)是PPF电容、电感的费用与其额定容量之间的函数关系；fA(S)是APF费用与其额定容量之间的函数关系。如下所示[9]：

fP(QP)=a0+a1QP

(2)

fA(S)=b0+b1SN

(3)

无源滤波器PPF对系统进行无功补偿，且流过的电流包括基波电流和有源滤波器输出的各次谐波电流，PPF的电容器容量QC为

(4)

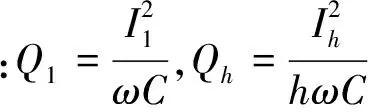
电感L容量QL为

(5)

QP=QC+QL

(6)

为避免系数选值的盲目性，使理论总投资费用更接近实际工程总投资费用, 采用市场价格决定法确定系数[9]：取a0=20，b0=60，a1=8，b1=24，单位为万元/Mvar。

有源滤波器APF在选择容量时，根据实测结果还要考虑10%～15%的裕量，即：

I1×ITHD(10%-15%)A

其容量S由所补偿的各次谐波电流值决定，与基波电流无关，其容量决定于所补偿的总谐波电流有效值，即：

(7)

(2)装设滤波装置后，使电网谐波含量在符合国家标注的基础上尽量低，以电网整个母线的谐波电压畸变率为衡量标准。

i=2，3，…

(8)

1.2 约束条件

(1)混合型有源滤波器在实际应用中，系统无功不能出现过补偿，否则在容性负载环境下，有源滤波器产生的补偿谐波和系统谐波的反相谐波容易在容性负载环境下产生谐振，被谐振放大的谐波反冲APF中的IGBT，导致其烧坏。而滤波器的导纳以容性为主，为了避免与系统发生谐振，保证系统的稳定性，以滤波器装置中电容器的容量与串并联谐振频率的关系[13]作为目标函数的约束条件：

(9)

(10)

式中：STf为变压器的容量；ZTf为变压器的标么值阻抗；Qc为PPF的电容器容量；Sfh为负荷容量；fs为串联谐振频率；fp为并联谐振频率；f基波频率；Ss为电源短路容量。

(2)SHAPF中的无源滤波器中的电容具有一定的无功补偿作用，配置滤波装置后既不能使系统出现无功功率过补偿现象，又要使系统的功率尽量接近于1，安装有源滤波器时应注意系统的无功补偿不能出现过补偿，即向系统输送无功功率。

(11)

Qmin、Qmax为无源滤波器提供的基波无功功率的上下限。

2 参数优化设计的改进粒子群算法

粒子群算法PSO(particle swarm optimizatio-n)[14，15]初始化为一群随机粒子，然后通过迭代找到最优解。在每一次迭代中，粒子通过跟踪个体极值pi和全局极值pg进行更新，标准的粒子群算法是一个反复迭代比较收敛的过程。

(12)

学习因子c1、c2使粒子保持着运动惯性，代表每个粒子推向pi、pg位置的统计加速项的权值，较低的值允许粒子被拉回前在目标区域外徘徊，较高的值导致粒子冲向或越过目标函数，使其具有扩展搜索空间趋势，有能力搜索新的区域。

2.1PSO参数分析

群体规模m取20～40。

速度vmax决定当前位置与最好位置之间的区域分辨率，如果太快，则粒子有可能越过极小点；如果太慢，则粒子不可能在局部极小点之外进行足够的搜素，会陷入局部极值区域内，这种限制可达到防止计算溢出。而惯性因子ω，大的惯性因子ω可使算法不易陷入局部最优，到算法的后期，小的惯性因子ω可使收敛速度加快，不至于出现振荡现象；动态减小惯性因子ω，可使算法更加稳定。

2.2 时变非线性三角函数控制

粒子群算法在进化初期收敛速度快，运算简单，但该算法在进化后期收敛慢、精度较差，容易陷入局部极值点[16～18]。根据参数速度vmax和惯性因子ω的特性以及之间的关系，PSO算法中参数速度vmax变大时，减小惯性因子ω可以防止粒子飞出搜索区域；速度vmax变小时，增大ω防止粒子在局部最优点徘徊，造成局部最优；且由于凹函数的递减特性优于线性递减的特性，而线性函数的递减特性优于凸函数的递减特性，因此为了提高粒子群算法的收敛性，避免算法陷入局部最优，本文改进的粒子群算法采用时变的非线性三角函数方法来控制参数如下式所示。

ωk=ωsin(vkθ)θ∈(-π，π)

(13)

改进的粒子群优化算法IPSO与PSO在经济费用适应度值进化过程性能上的比较如图2所示。

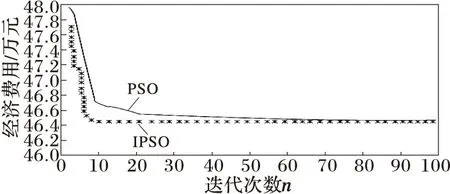
图2 IPSO与PSO适应度值的进化过程比较

如图2 所示，采用了改进的PSO算法，加快了算法的收敛速度，避免算法陷入局部最优，明显优于PSO算法。

2.3 适应度函数的构造

并联混合型有源滤波器在满足经济性最小情况下同时满足滤波效果、无功功率、串并联谐振条件。根据优化的目标函数，粒子个体适应函数为

F=C-minf≥0

(14)

其中C为一较大正数；

(15)

(16)

3 实例分析

本文以重庆市某变电站为研究对象，10 kV母线处的电能质量电压总畸变率THDU=9.096%gt;4%，谐波电压为5、7、20次，谐波测试值大于国标GB/T 14549-93，相应各次限值不满足要求，谐波电流如表1所示。

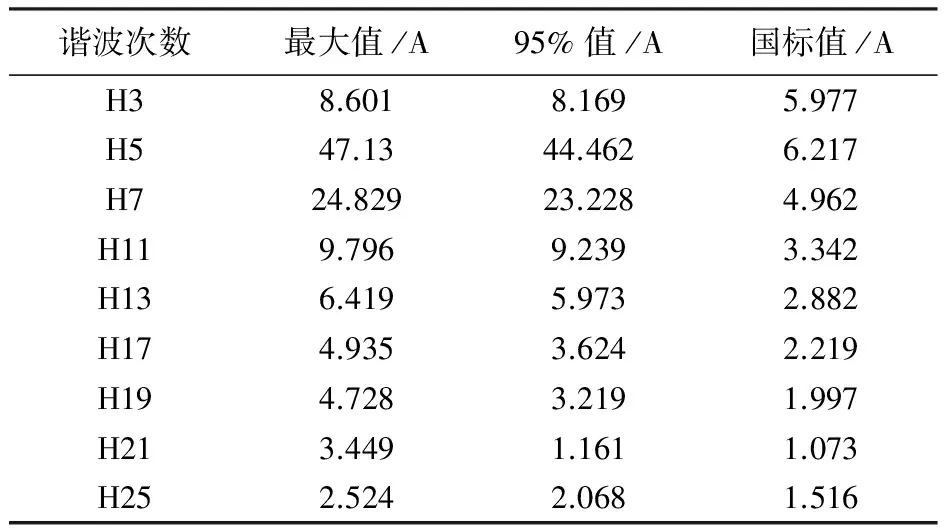
表1 10 kV低压母线A相谐波电流

SHAPF的无源部分装设3次、5次、7次单调谐滤波器和高通滤波器，运用Matlab软件对优化方法进行编程实现。为验证优化方法的有效性，根据优化配置的参数，采用Matlab进行仿真分析。SHAPF投入前后电网电流的仿真图形、频谱如图3～5所示。

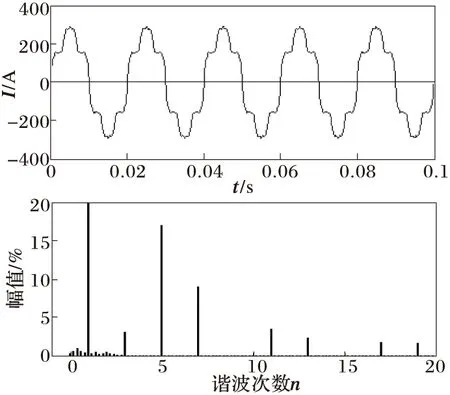
图3 负载电流波形和频谱

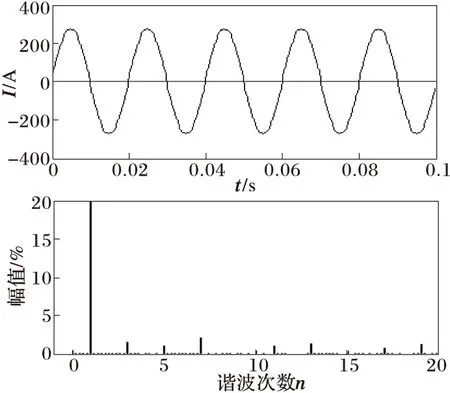
图4 传统设计的滤波器滤波后电流波形和频谱

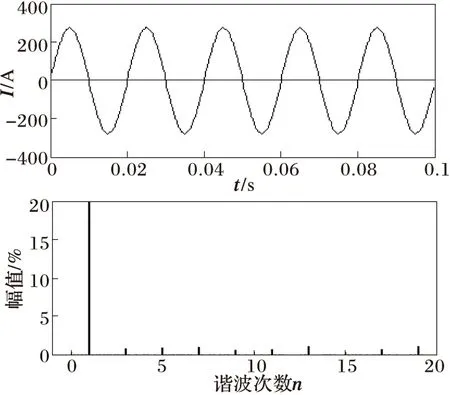
图5 优化设计的滤波器滤波后电流波形和频谱

从图3～5可以看出在补偿投入后，电流波形有很大的改善，改进的优化设计采用电容无功补偿功率与串并联谐振频率的关系作为约束条件对混合型有源滤波器PPF调谐滤波器参数进行优化配置较传统经验方法具有优越性。两种方法设计的参数结果比较如表2所示。

表2 PPF参数的配置结果比较

传统经验方法参数配置的混合型有源滤波器，经阻抗频谱分析仪测试产生了频率为7次谐振，严重影响了电网的供电质量。经优化参数配置的混合有源滤波器在重庆市实际系统进行了应用， 有效的避免了谐振的发生，确保了混合有源滤波器安全稳定的运行。

4 结语

(1)提出采用电容补偿功率与串并联谐振频率的关系为谐振约束条件，对并联混合型有源滤波器进行优化配置，避免了过补偿及谐振问题。

(2)根据速度v和惯性因子w的关系，提出改进的算法采用非线性三角函数时变的方法来控制参数，加速了优化算法的收敛速度, 避免算法陷入局部最优。

(3)应用改进的优化算法和约束条件对混合型有源滤波器参数的优化配置具有一定的优越性。

[1] 罗安.电网谐波治理和无功补偿技术及装备[M].北京：中国电力出版社，2006.

[2] 赵伟, 罗安,范瑞祥,等(Zhao Wei, Luo An, Fan Ruixiang,etal). 谐波电压对中高压并联混合有源滤波器影响及注入支路参数设计(Influence of harmonic voltage on shunt HAPF for high power grid and injection branch parameters design)[J].中国电机工程学报(Proceedings of the CSEE),2008,28(9):29-36.

[3] 范瑞祥,马亮,罗安,等(Fan Ruixiang , Ma Liang, Luo An,etal).背景谐波电压对混合型有源滤波器的影响及对策(Influences and countermeasures of background harmonic voltages on a hybrid active power filter)[J].电力系统自动化(Automation of Electric Power Systems),2008,32(1):98-102.

[4] 范瑞祥,罗安,周柯,等(Fan Ruixiang , Luo An, Zhou Ke,etal). 并联混合型有源电力滤波器的建模和控制策略分析(The modeling and the control strategy analysis of shunt hybrid active power filters)[J].中国电机工程学报(Proceedings of the CSEE), 2006 ,26(12):55-61.

[5] 范瑞祥,罗安,李欣然(Fan Ruixiang, Luo An, Li Xinran). 并联混合型有源电力滤波器的系统参数设计及应用研究(Parameter design and application research of shunt hybrid active power filter)[J].中国电机工程学报(Proceedings of the CSEE), 2006,26(2):106-111.

[6] 何娜,黄丽娜,武健,等(He Na, Huang Lina, Wu Jian,etal). 基于粒子群优化算法的混合有源滤波器中无源滤波器的多目标优化设计(Multi-objective optimal design for passive part of hybrid active power filter based on particle swarm optimization)[J]. 中国电机工程学报 (Proceedings of the CSEE), 2008,28(27):63-69.

[7] 夏向阳，罗安，周柯(Xia Xiangyang, Luo An, Zhou Ke)．混合型有源电力滤波器的设计与仿真(Design and simulation of hybrid active power filter)[J]．高电压技术(High Voltage Engineering)，2006，32(2)：67-69.

[8] Kim Sangsun, Enjeti P N. A new hybrid active power filter(APF)topology[J].IEEE Trans on Power Electronics,2002,17(1):48-54．

[9] 余健明，李春莹(Yu Jianming, Li Chunying).基于多谐波源动态运行的配电网滤波装置优化配置(Optimal filter allocation of distribution network based on multiple harmonic sources dynamic running)[J].电网技术(Power System Technology),2005,29(6):22-26.

[10]吴竞昌.供电系统谐波[M].北京：中国电力出版社, 2006.

[11]杨文宇，刘健，余健明，等(Yang Wenyu, Liu Jian, Yu Jianming,etal).改进的自适应遗传算法在配电网谐波抑制中的应用(Optimal allocation of harmonic filters in distribution network based on improved adaptive genetic algorithm)[J].继电器 (Relay), 2004, 32(4):24-27,35.

[12]Wakileh G H.电力系统谐波-基本原理、分析方法和滤波器设计[M].徐政译.北京：机械工业出版社， 2003.

[13]Jos Arrillaga Neville R.电力系统谐波[M].2版.林海雪，范明天，薛惠，译.北京：中国电力出版社，2006.

[14]Kennedy J，Eberhart R．Particle swarm optimization[C]//IEEE International Conference on Neural Networks, Perth, Australia: 1995.

[15]刘自发, 张建华(Liu Zifa, Zhang Jianhua). 基于改进多组织粒子群体优化算法的配电网络变电站选址定容(Optimal planning of substation locating and sizing based on refined multi-team PSO algorithm) [J]. 中国电机工程学报(Proceedings of the CSEE), 2007,27(1):105-111.

[16]王波,邰能灵,翟海青,等(Wang Bo, Tai Nengling, Zhai Haiqing,etal).基于混合粒子群算法的短期负荷预测模型(Hybrid optimization method based on evolutionary algorithm and particle swarm optimization for short-term load forecasting)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA )，2008,20(3): 50-55.

[17]俞俊霞，赵波(Yu Junxia, Zhao Bo). 基于改进粒子群优化算法的最优潮流计算(Improved particle swam optimization for optimal power flow problems)[J]. 电力系统及其自动化学报(Proceedings of the CSU-EPSA ),2005,17(4):83-88.

[18]黄辉先，陈资滨(Huang Huixian, Chen Zibin).一种改进的粒子群优化算法(Novel arithmetic based on particle swam optimization)[J].系统仿真学报(Journal of System Simulation ),2007,19(21):4922-4925.

夏向阳(1968-)，男，博士后，副教授，研究方向为分布式发电技术和电能质量控制等。Email:xia_xy@126.com

徐林菊(1984-)，女，硕士研究生，研究方向为电力电子技术与电能质量。Email:xlj20081011@163.com

OptimizationoftheHybridActivePowerFilterParametersConsideringHarmonicResonance

XIA Xiang-yang1， XU Lin-ju1， LIU Fei-long2

(1.College of Electrical Engineering, Changsha University of Science and Technology, Changsha 410004, China；2.Datang Corporation Leiyang Power Plants, Leiyang 421856, China)

As to the problems of reactive power overcompensation and resonance in the design of the hybrid active power filter, the relationship between capacitive reactive power compensation and series-parallel resonant frequency is proposed as the constraints to optimize the parameters of shunt hybrid active power filter (SHAPF). The improved particle swarm optimization (IPSO) algorithm is adopted, and a method of nonlinear time-varying trigonometric function is proposed to control the parameters based on the relationship between speedvand the inertia factorwof PSO algorithm to accelerate the convergence speed and prevent falling into local optimum. Matlab is used for simulation and the parameters of SHAPF have been optimized which has a good filtering effect and the resonance is avoided effectively in the application, with some engineering application values.

capacitor power； series-parallel resonant frequency； reactive power overcompensation； time-varying nonlinear trigonometric function； optimization of the parameters

TM713

A

1003-8930(2012)06-0031-05

2011-11-29；

2011-12-21

广东省科技计划项目重大科技专项(2010A080804023)；湖南省自然科学基金项目(2011JJ5027)；湖南省科技计划项目(2011GK3118)