一种带有交易成本的保底型基金的定价
2012-11-08朱海燕张寄洲
朱海燕, 张寄洲
(1.连云港师范高等专科学校, 江苏 连云港 222006; 2.上海师范大学 数理学院, 上海 200234)
一种带有交易成本的保底型基金的定价
朱海燕1, 张寄洲2
(1.连云港师范高等专科学校, 江苏 连云港 222006; 2.上海师范大学 数理学院, 上海 200234)
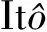
交易成本; 随机利率; Hull-White模型
0 引言
随着人们金融意识的不断增强,单纯的股票市场、债券市场和银行储蓄已不能满足人们在投资理财方面的需求.针对人们不同的风险偏好和投资回报期望,近年来,金融机构推出了很多满足不同需求人群的各种不同类型的金融产品,以满足人们投资理财的需要.无论对出售方来说还是对投资者而言,能正确地评估这种金融产品的实际价值都是非常重要的.
保底型基金由于既可以保证投资者最低收益(通常低于同期国债的收益),同时又可能获得高额的投资回报(超额部分按一定比例的分红),满足了一部分投资者的需要,所以目前在市场上很受欢迎.文[1]讨论了利率服从Vasicek模型和市场无任何摩擦情形下的保底基金的设计原理和定价方法.文[2]针对现实市场上投资者将面临数量可观、不容忽视的交易成本,给出了有交易成本的欧式期权定价方法.而本文模型的理论基础是Hull-White利率期限结构模型[3](作为Vasicek模型的推广,其参数均为时间t的函数),在交易过程中支付一定的交易费用,这样就使这种理财产品更贴近我们的市场实际,从而更具实用价值.
1 数学模型
1.1 基本假设
1) 资产的构成:每份基金的面值为1元;
2) 根据基金公司是否获得金融机构进行担保,设计如下条款:
如果有金融机构进行担保,那么
a) 基金到期保底收益为每份α元,超额收益部分的分红比例为β(0≤β≤1);
b) 基金全部投资于指数基金(如股票);
如果没有金融机构进行担保,那么,为确保公众投资者的保底收益,发起人必须投入一部分自有资金,它在基金中所占比例为1-ω,同样规定上述条款,但增加第三条款:
c) 当基金投资发生亏损时,对基金净值设置一个下限K(t).当基金净值触及K(t)时,基金全部投资于T时刻到期的零息票国债,从而确保投资者T时刻的保底收益.其中K(t)=ωαP(r,t).这里,P(r,t)为T时刻到期的零息票国债在t时刻的价格.
3) 市场利率模型:我们采用服从均值回归的Hull-White模型
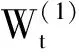
其中θ(t)是初始期限结构有关的参数,a(t),σr(t)是波动率的参数,他们均是时间t的函数.该模型所描述的利率运动形态是认为利率具有稳定的长期运动趋势θ(t),在不同时刻t,rt以a(t)的速度向趋势靠近,这种性质即为均值回归性.
4) 对于指数型基金(如股票):假定其净值服从几何Brown运动

5) 支付交易费用:交易费用可看作是投资者因买卖标的资产(股票)而产生的直接费用,一般由多头支付,并通常以交易额的固定比例K来表示.考虑时段[t,t+δt],δt是小量,但不趋于0,此时利率r相对固定,可看成常数.为了对冲发行基金所带来的风险,每隔δt时段就要调整一次用来对冲的标的资产(股票)的份额δΔ(δΔ>0买进,δΔ<0卖出),则产生的交易成本为K|δΔ|Vt.
6) 假设客户持有的每份保底基金的价值Ct是关于时间、利率和指数基金价值的函数,即Ct=C(Vt,rt,t),并记在T时刻到期日的零息票债券价格为Pt=P(rt,t).
1.2 建立方程

δΠt=δCt-Δ1δVt-Δ2δPt-KVt|δΔ1|=
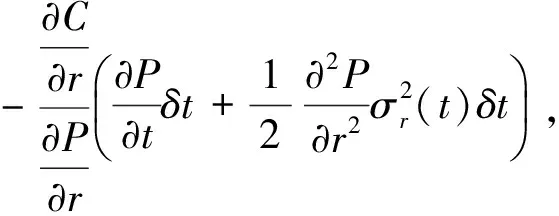
因保值调整策略而产生的交易份额δΔ1为

其中Φ~N(0,1).因此交易费用的数学期望为

进一步得到δΠ的数学期望为
根据无套利原理,此时E(δΠ)=r(t)Πδt=r(t)(Ct-Δ1Vt-Δ2Pt)δt.整理得

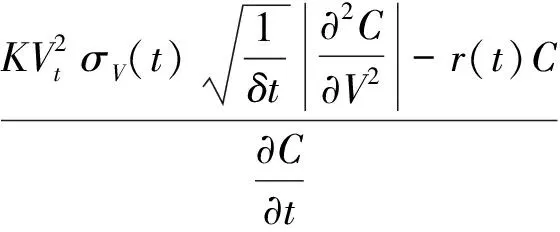
引入风险的市场价格λ(t), 在Hull-White模型下有
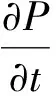
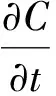
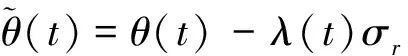
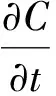
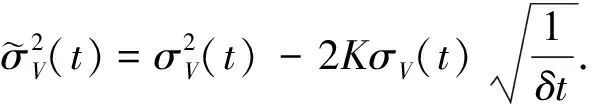
1.3 定解问题
如果有银行提供担保,不存在违约,此时金融机构无需提供自有资金,在
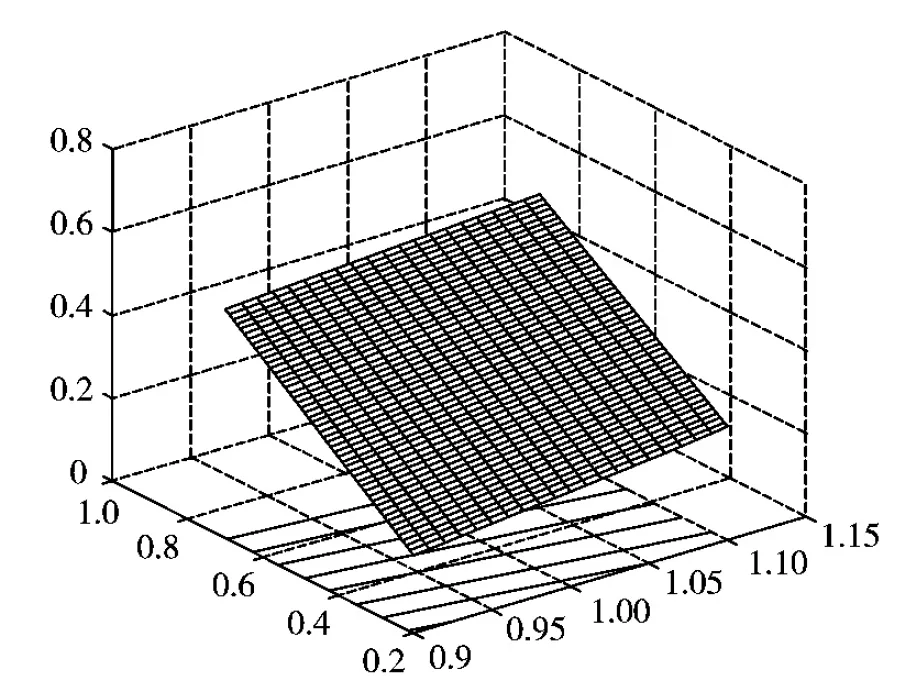
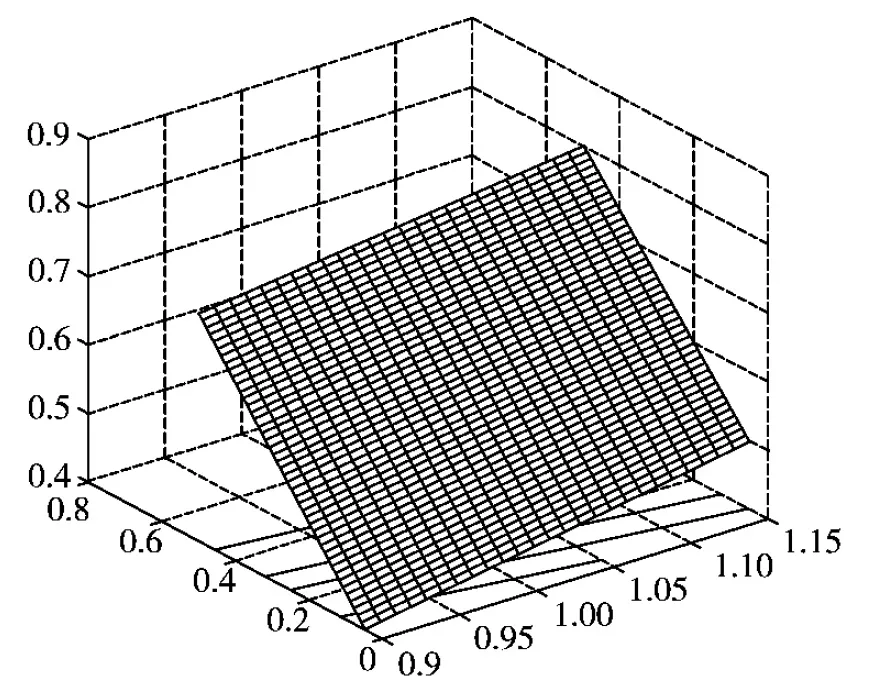
Σ:-∞ (1) 如果没有银行提供担保,存在违约可能性,此时金融机构必须提供自有资金,根据基金条款(3),在Σ:-∞ (2) 其中到期日为T的零息票价格P满足下列边值问题(见文献[4]) (3) 定解问题(3)有唯一显式解P(rt,t,T)=eA(t)-B(t)r(t), 其中 令 在此变换下,经计算化简可将LC变为 其中 σ2(t)(t)+(t)-2ρσr(t)σV(t), 于是 1) 对于有银行或其他金融机构担保情况,在上述变换下,原定解问题(1)变为 此时未定权益W是现金流α与β份敲定价格为α的看涨期权的和,于是有(见文 [5]) 其中 故 2) 对于没有银行或其他金融机构担保情况,在上述变换下,定解问题(2)变为 (4) (5) 于是定解问题(5)变为 (6) 再令 其中 则定解问题(6)变为 (7) 为求解定解问题(7),利用镜像法,定义 则由Poisson公式可得 故 其中 在均值回归Hull-White利率模型及股指服从几何Brown运动,并支付一定交易费用的情形下,我们得到了与股指挂钩的保底分红基金(有担保和无担保两种情况)的显式定价公式.通过数值分析,我们进一步发现,在假设条件更具一般性的假设下,结果与实际将更加吻合. 图1 无交易费有担保情形 图2 有交易费有担保情形 [1] 任学敏,李少华. 保底型基金的设计与定价[J]. 系统工程理论与实践,2005,9:22-28. [2] Hull J C, Options Futures and Other Derivatives[M]. China: Tsinghua University Press, 2001. [3] Kwok Y K, Mathematical Models of Financial Derivatives[M]. Springer: Singapaore, 1998. [4] Hull J,W. Pricing Interest Rate Derivative Securities[M]. Review of Financial Studies,1990,3: 573-592. [5] 姜礼尚. 期权定价的数学模型和方法[M]. 北京:高等教育出版社,2003. [责任编辑:李春红] ThePricingofaFundaboutPromisedLowestReturnwithTransactionCosts ZHU Hai-yan1, ZHNAG Ji-zhou2 (1.Department of Mathematics and Applied Mathematics, Lianyungang Teachers College, Lianyungang Jiangsu 222006, China)(2.College of Mathematics and Sciences, Shanghai Normal University, Shanghai 200234, China) transaction costs; stochastic interest rate; hull-white model CP31, F224 A 1671-6876(2012)03-0235-06 2012-06-06 朱海燕(1978-), 女, 江苏盐城人, 讲师, 硕士, 研究方向为应用微分方程.2 定解问题求解
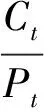



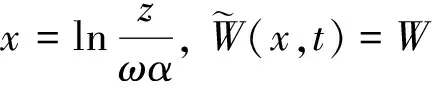

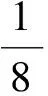
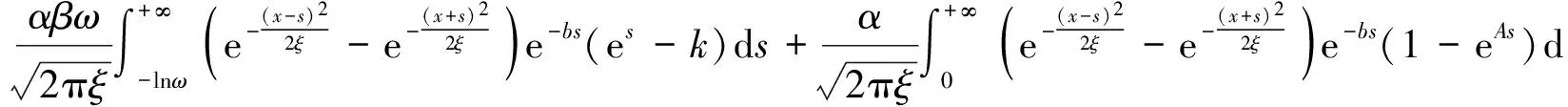

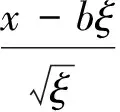
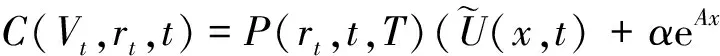
3 数值分析举例

4 结论