基于当地流活塞理论的翼-身组合体飞行器大攻角超声速颤振分析
2012-11-08史晓鸣杨炳渊李海东唐国安
史晓鸣,杨炳渊,李海东,唐国安
(1.复旦大学 力学与工程科学系,上海 200433;2.上海航天技术研究院 第八设计部,上海 200233)
0 引 言
随着大机动、大过载的要求以及新的发射方式的应用,飞行攻角显著增加。通常在大攻角飞行时颤振边界降低,颤振危险性比零攻角时更为突出,掌握飞行器大攻角颤振分析方法对于工程设计具有重要的现实意义。大攻角颤振分析的关键在于非定常气动力的计算,大攻角颤振气动力是一个高度复杂的非线性非定常流动问题,势流理论将不再适用[1-2]。非定常CFD技术能真实地模拟大攻角非定常流场的特征,能考虑组合体部件间的干扰和大攻角带来的非线性,但其计算规模大、耗时多、效率低下,在工程设计中全面推广仍存在很多困难[3]。目前工程设计中常用的非定常气动力计算方法有核函数法、面元法、超声速格网法、细长体理论、活塞理论和干扰因子法等[4-5],这些气动力模型都是以势流理论为基础的线化模型,不能考虑大攻角情况,部件间干扰的处理也比较粗糙,不能完全满足工程设计的需求。
飞行器工程设计迫切需要一种既能适合于较大攻角复杂外形飞行器颤振非定常气动力计算,又能快速得到计算结果的方法。而上世纪90年代至今发展起来的当地流活塞理论[6-7]及其与CFD技术的结合[8-9],较好地解决了大攻角翼面的非定常气动力的计算问题。本文基于当地流活塞理论推导了旋成体机身和任意外形三维机翼非定常气动力计算公式,利用CFD数值求解定常流场当地流参数,使当地流活塞理论推广用于大攻角三维机翼和旋成体机身,并可考虑部件间的干扰,从而可进行全机组合体大攻角颤振计算。以翼-身组合体外形飞行器为例,完成了Ma=2~7,攻角α=0°~20°的颤振计算,计算结果经与非定常气动力采用CFD数值方法计算的CFD/CSD直接耦合的颤振计算结果对比,精度满足工程设计需要,其计算速度却提高了百倍以上。
1 翼-身组合体飞行器的动力学模型
考虑由机身、机翼、垂尾组成的面对称布局翼-身组合体。忽略结构阻尼,由分枝模态法可导出结构的运动微分方程[10-11]:

式中,M和K分别为结构的模态质量和模态刚度矩阵,QA为广义气动力矢量,由机身、机翼、垂尾各部件的广义气动力组成:
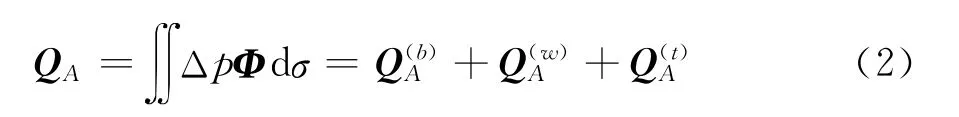
式中Δp为飞行器表面非定常压力分布,Φ为各个分枝模态振型函数组成的列矢量。
2 非定常气动力
本节讨论式(2)中机身、机翼、垂尾各个部件的非定常气动力计算方法。考虑图1所示飞行器表面任意曲面,过曲面上任意点o作切面P,假设当地流速度VL沿切面的任一方向,以o为原点作局部坐标系oξηζ,其中ξ轴方向与VL方向重合,ζ轴与过o点的外法线方向重合。由当地流活塞理论,曲面上任意点的非定常气动力为:
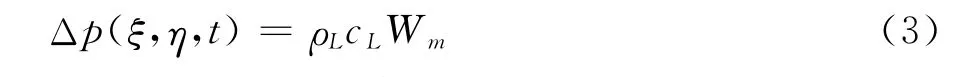
式中ρL、cL为曲面任意点的当地气流密度和声速,Wm为物面扰动引起的下洗。假设垂直于物面的振动表示为ζ=ζ(ξ,η),则物面振动速度和转角引起的下洗为
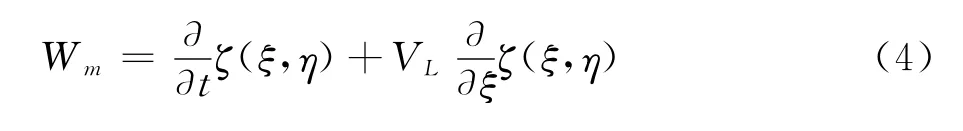
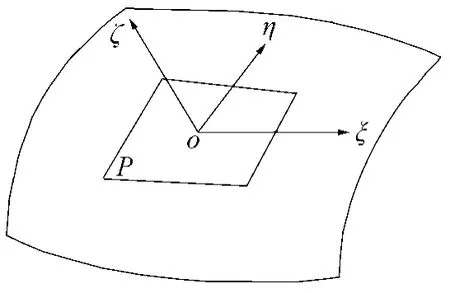
图1 任意曲面上的局部坐标系Fig.1 Local coordinate system
对于常见的轴对称旋成体机身,采用图2所示的柱坐标系,表面方程可用母线方程r=R(x)表示,机身垂直于机身轴线的振动为Z=Z(x,t),其外法线对z轴的方向余弦为

式中μb=[1+(∂R/∂x)]-1/2为机身母线切线与x轴夹角的余弦,因此垂直于机身表面的振动为

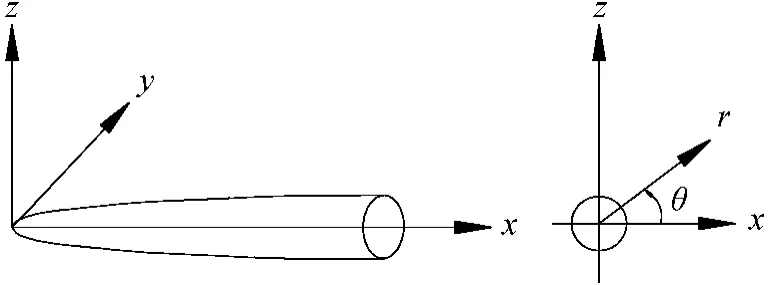
图2 机身坐标系Fig.2 Coordinate system of fuselage
对于如图3所示翼面,则采用机翼局部坐标系,设对称翼型的翼面以中性面为参考平面的型面方程为H=H,),以离开中性面为正,翼面垂直于中性面振动为=(,t)。则垂直于翼型面上、下表面的振动:
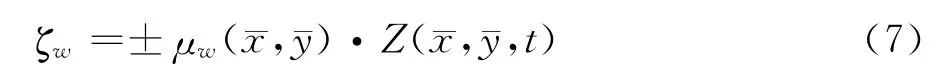
式中上翼面取正号,下翼面取负号,μw=[1+(∂H/∂)2+(∂H/∂)2]-1/2为该点翼型面外法线对轴的方向余弦。
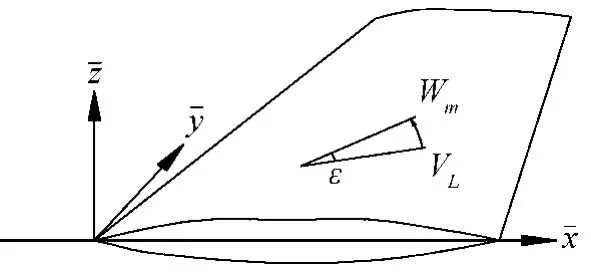
图3 翼面坐标系Fig.3 Coordinate system of wing
式(6)和(7)代入式(4),并利用方向导数公式,可得垂直于机身表面的下洗
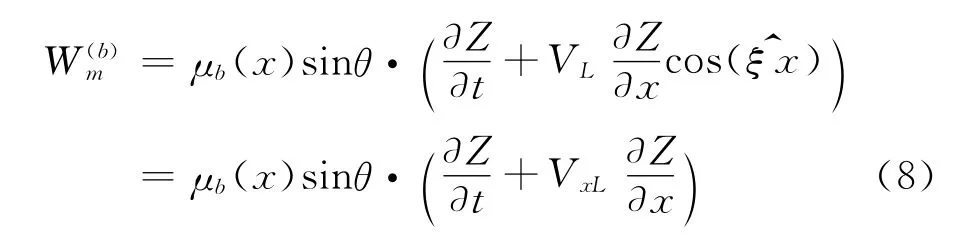
以及垂直于机翼上、下表面的下洗
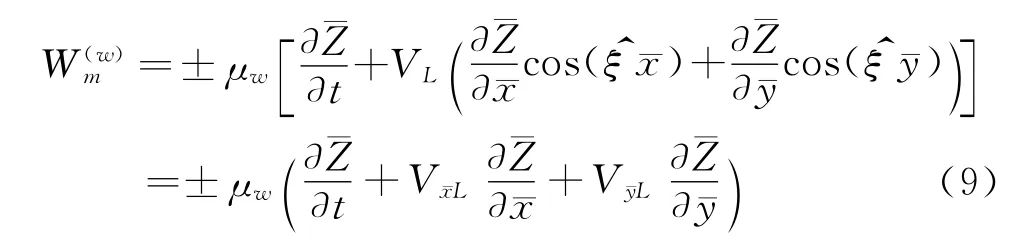
式(8)、(9)中,式中VxL为机身表面当地气流速度在x向的分量;VL、VL分别为机翼表面当地气流速度的、向分量。同理可得垂尾与式(9)相同的下洗表达式,只是式中坐标替换为x替换为z,位移替换为Y。将机身、机翼和垂尾的下洗代入式(3)得到非定常压力分布,再代入式(2),并做模态坐标变换,可得广义气动力Q、Q和Q。
通过CFD数值仿真求解不同马赫数不同攻角下飞行器定常流的方法即可获得式(3)、(8)、(9)中的当地流参数。因此,各种复杂外形飞行器部件之间的互相干扰、流场三维效应以及大攻角的非线性等都可在当地流参数中得到反映,从而使得当地流活塞理论能够适应复杂外形飞行器和部件的大攻角非定常气动力计算和颤振计算,计算精度得以提高而且时间成本大大下降。
3 算例与分析
以文献[10]已完成模态计算的面对称布局翼-身组合体飞行器为本文算例,各分枝模态如下选取:对称分枝取刚体沉浮、俯仰和前三阶弹性模态;反对称分枝取刚体滚转和前四阶弹性模态;垂尾分枝取前五阶弹性模态。表1给出各分枝模态频率,振型可参见文献[10]。采用频域复特征值方法搜索颤振临界参数。
用本文结合CFD的当地流活塞理论方法完成了海平面高度下,Ma=2~7,攻角α=0°~20°的全机组合体颤振计算。图4为Ma=4来流下不同攻角的颤振边界,图中同时给出非定常气动力采用全数值仿真计算的CFD/CSD直接耦合方法的计算结果,本文结果与其相比,在临界动压数值上最大误差为28.46%,换算为临界速度的最大误差仅13.14%,计算精度满足工程设计要求。本文方法一个马赫数点的计算时间在1h左右,而CFD/CSD全数值仿真方法的计算时间超过100h,在满足精度要求的情况下,计算效率提高100倍以上,更适合于在工程设计中应用。图5为不同来流马赫数和攻角下的颤振边界,从中可见攻角对颤振边界的影响不可忽略,尤其是来流为高马赫数时,攻角增大使得颤振边界大幅下降。
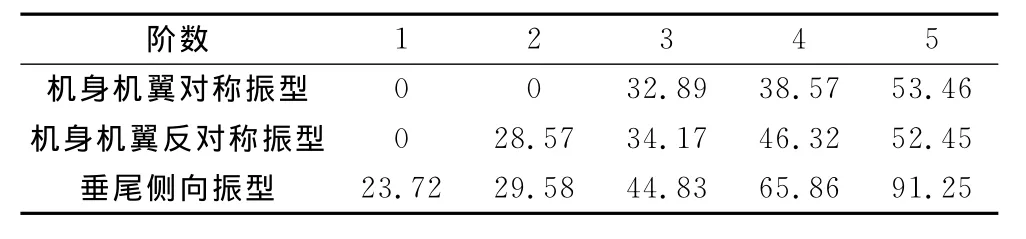
表1 各个分枝结构固有频率(Hz)Table 1 Frequencies of each branch(Hz)
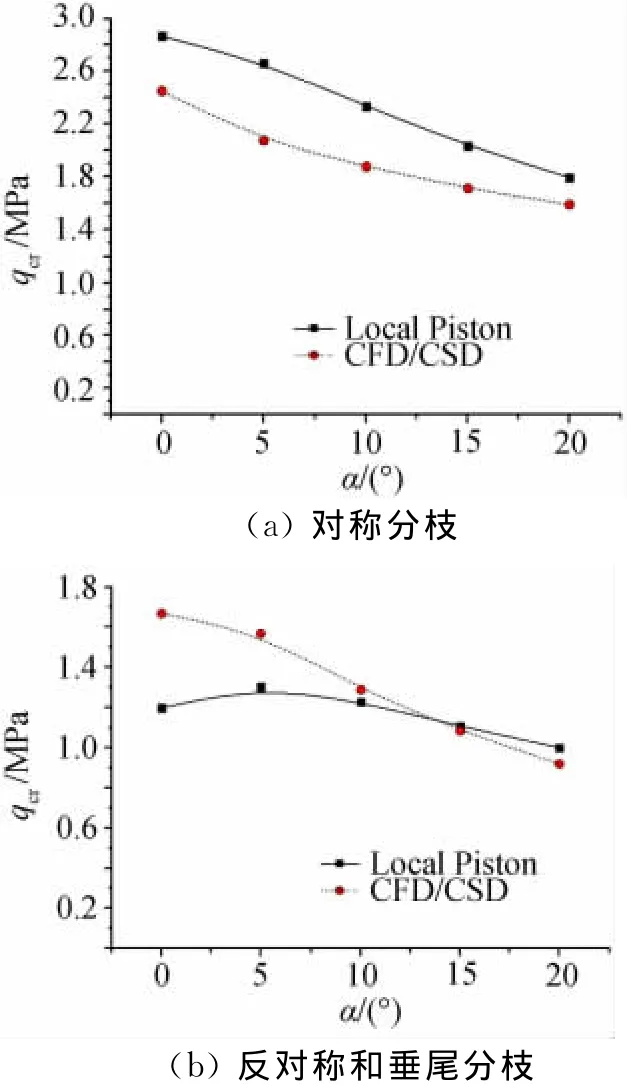
图4 Ma=4来流状态下不同攻角颤振边界Fig.4 Flutter critical dynamic pressure at different angles of attack when Ma=4
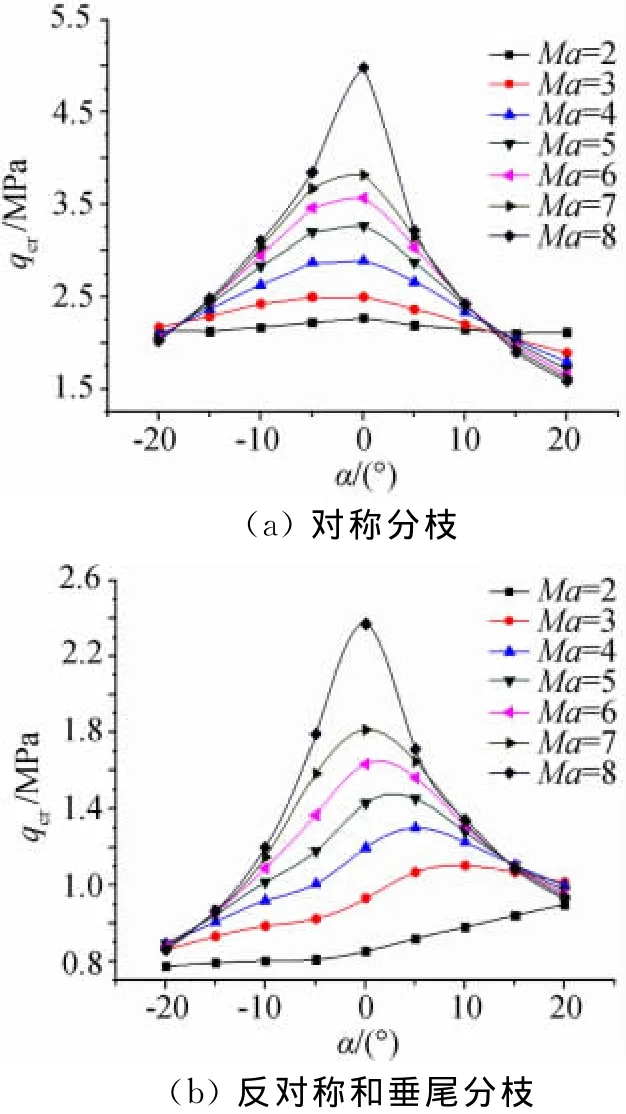
图5 不同马赫数下颤振边界随攻角变化Fig.5 Flutter critical dynamic pressure at different angles of attack and Mach numbers
4 结 论
以当地流活塞理论为基础,假设当地流沿飞行器表面任意切线方向,推导了旋成体机身和任意外形三维机翼非定常压力分布计算公式,结合CFD数值求解定常当地流参数,形成了可用于全机组合体大攻角超声速颤振计算的方法。算例结果表明本文方法计算精度接近全CFD/CSD数值仿真方法,计算效率则大幅度提高,适合工程设计计算要求。
算例结果显示攻角对颤振边界有很大影响,飞行器设计中需充分予以考虑。尤其是高马赫数时,攻角增大使得颤振边界大幅下降。
[1]杨炳渊,史晓鸣,梁强.高速有翼导弹多场耦合动力学的研究和进展(上)[J].强度与环境,2008,35(5):55-63.(YANG Bing-yuan,SHI Xiao-ming,LIANG Qiang.Investigation and development of the multi-physics coupling dynamics on the hypersonic winged missiles (I)[J].Structure&EnvironmentEngineering,2008,35(5):55-63.)
[2]叶正寅,谢飞.中等及大迎角下的翼型气动弹性性质研究[J].风机技术,2009,(2):9-13.(YE Zheng-yin,XIE Fei.Research on the aeroelastic characteristics of an airfoil in moderate and high incidences[J].Compressor,Blower&FanTechnology,2009,(2):9-13.)
[3]SCHUSTER D M,LIU D D.Computational aeroelasticity:success,progress,challenge[J].Journal of Aircraft,2003,40(5):843-856.
[4]McNAMARA J J,FRIEDMANN P P.Aeroelastic and aerothermoelastic analysis of hypersonic vehicles:current status and future trends[R].AIAA 2007-2013.
[5]CHAE S,HODGES D H.Dynamics and aeroelastic analysis of missile[R].AIAA 2003-1968.
[6]杨炳渊,宋伟力.应用当地流活塞理论的大攻角升力面颤振气动力表达式[J].力学季刊,1999,20(3):223-228.(YANG Bing-yuan,SONG Wei-li.Expressions about aerodynamic forces of flutter for wing with high angle of attack by local flow piston theory[J].ChineseQuarterly ofMechanics,1999,20(3):223-228.)
[7]杨炳渊,宋伟力.前缘激波脱体的大迎角翼面颤振工程计算方法[J].振动与冲击,2002,22(4):100-103.(YANG Bing-yuan,SONG Wei-li.Engineering approximation of high attack angle flutter for wing with bow wave on leading edge[J].JournalofVibrationand Shock,2002,22(4):100-103.)
[8]张伟伟,叶正寅.基于当地流活塞理论的气动弹性计算方法研究[J].力学学报,2005,37(5):632-639.(ZHANG Wei-wei,YE Zheng-yin.Numerical method of aeroelasticity based on local piston theory[J].Acta MechanicaSinica,2005,37(5):632-639.)
[9]ZHANG Wei-wei,YE Zheng-yin,ZHANG Chen-an.Supersonic flutter analysis based on a local piston theory[J].AIAAJournal,2009,47(10):2321-2328.
[10]史晓鸣,许泉,唐国安.基于分枝模态法的面对称布局飞行器结构动力学建模[J].上海航天,2011,28(2):27-31.(SHI Xiao-ming,XU Quan,TANG Guo-an.The dynamics modeling of plane symmetrical vehicle structural based on branch mode method[J].AerospaceShanghai,2011,28(2):27-31.)
[11]杨炳渊,史晓鸣,梁强.高速有翼导弹多场耦合动力学的研究和进展(下)[J].强度与环境,2008,35(6):56-62.(YANG Bing-yuan,SHI Xiao-ming,LIANG Qiang.Investigation and development of the multi-physics coupling dynamics on the hypersonic winged missiles (II)[J].Structure&EnvironmentEngineering,2008,35(6):56-62.)
