受宽带噪声激励的二元机翼随机振动系统的矩Lyapunov指数

黄 勇， 刘先斌

（南京航空航天大学 机械结构力学及控制国家重点实验室，江苏 南京210016）

0 引 言

在所有气动弹性问题中，颤振问题无疑是在科学和工程上最受关注的问题之一［1］。这不仅仅是由于这种气动弹性稳定性问题具有重大的实际意义和应用价值，而且还由于它具有深刻的数学物理内涵。一直以来，人们对在随机气流激励下的飞行器颤振行为十分关注，这是因为飞行器颤振是由结构非线性和气动非线性相耦合而导致的复杂的非线性动力学行为，随机激励（尤其是参数激励）的介入会导致随机失稳和随机分岔等复杂的随机动力学行为。

对于确定性机翼颤振，国内外学者已进行了大量的研究。而对于机翼随机颤振的研究由于其动力学行为的复杂性，目前的研究成果还十分有限。近年来，随着非线性随机振动理论的不断发展，基于FPK方程的半解析概率方法正在越来越多地被人们用来处理随机颤振问题。较为著名的有Ibrahim等人［2－3］的工作，通过将面内载荷和气压分量设为不相关的、零均值宽带随机过程，他们使用FPK方程方法和累积量截断方法，研究了超声速气流中的壁板受面内随机激励的颤振机理。D.Poirel和S.J.Price［4－5］研究了考虑气动弹性和湍流随机扰动的随机颤振，得到的结果从概率统计的角度能更好地解释机翼颤振的机理。然而工程应用中人们还常常会关心系统响应的一、二阶统计矩稳定性，这从随机颤振的早期研究内容可以得到证实。

矩Lyapunov指数对于随机分岔研究的意义在于，最大Lyapunov指数只是矩Lyapunov指数关于p的一阶项的系数，因此根据系统的矩Lyapunov指数同样可以得到D－分岔点［6］以确定系统的概率1稳定的边界。此外，针对某些系统，矩Lyapunov指数还可以确定其P－分岔点。因此相较于系统的最大Lyapunov指数，矩Lyapunov指数具有更重要的动力学意义，但是有关系统矩Lyapunov指数的计算却比最大Lyapunov指数的计算困难得多。

矩Lyapunov指数是随机动力系统研究的重要部分，其定义如下：

这里x（t，x0）是随机动力系统的解，E［·］表示数学期望，‖x（t，x0）‖表示向量范数。如果Λ（p，x0）＜0，那么由定义可知，当t→∞时，E［‖x（t，x0）‖p］→0，说明系统是p阶矩稳定的。矩Lyapunov指数的概念是由Arnold［7］在研究线性随机动力系统时提出的，并且得到在一定条件下，上式极限存在，是与x0独立的关于p的凸解析函数，因此矩Lyapunov指数可以表示为Λ（p），Λ（p）／p是递增的，且：

是最大Lyapunov指数。而Λ（p）＝0的一个非零解δp称为矩Lyapunov指数的稳定性指标。之后，Arnold在文献［7］中分别获得了实噪声和白噪声激励下线性随机系统的完整结果。Kozin and Sugimoto［8］研究了线性Itô微分方程非平凡解的矩稳定性和几乎肯定稳定性的联系，得到了在参数空间中几乎肯定稳定区域是p阶矩稳定区域在p→0时的极限。

尽管矩Lyapunov指数在研究随机动力系统的稳定性中是非常重要的，但在实际情况下，研究起来很困难，关于它的研究结果也很有限，而且大部分的研究结果都是基于渐近的解析方法，如随机平均法、摄动方法等获得的。对在白噪声和实噪声激励下的两维和四维系统，Arnold等［9］和 Namachchivaya［10］等获得了矩Lyapunov指数关于小噪声和小p的渐近展开，Khasminskiihe和 Moshchuk［11］研究了白噪声激励下，系统矩阵有两个纯虚特征值的二维系统，对有限的p值，证明了p阶矩Lyapunov指数能展开为小噪声强度的级数。对实噪声激励下的四维系统，应用Arnold在文献［7］介绍的扰动展开方法，Sri Namachchivaya和 Roessel［12］获得了矩 Lyapunov指数关于小扰动参数的展开。Xie［13］应用与Khasminskiihe［11］类似的方法获得了二维系统在实噪声和有界噪声激励下矩Lyapunov指数、Lyapunov指数和稳定性指标关于小扰动参数的渐近展开。刘先斌［14］等讨论了受实噪声参数激励的 Van der Pol－Duffing振子的有限p阶矩Lyapunov指数。在他们的工作中，实噪声激励被取为一个定义于有界闭区域上的n维Ornstein－Uhlenbeck过程的光滑非线性函数，并最终计算了p阶矩Lyapunov指数的渐近展式。

本文主要研究了随机宽带噪声作用下，机翼颤振系统的矩Lyapunov指数及其相应的稳定性指标，推导出系统矩Lyapunov指数的近似解析解，并讨论了所有系统参数对系统矩Lyapunov指数的影响。

1 运动方程

二元机翼具有两个自由度，其广义坐标通常选取为上下平移h及俯仰角θ（如图1所示）。在考虑定常气动力作用时，具有粘性阻尼及立方俯仰刚度的颤振系统的无量纲运动方程为（详细推导过程参见文献［15－16］）：

式中，μ＝，ρ为空气密度，m为机翼质量，b为半弦长，d＝，ab为弹性轴E在半弦点后的距离，xθb是重心G在弹性轴E后的距离，rθb是机翼对弹性轴的回转半径，ch、cθ分别为无量纲俯仰和扭转阻尼系数，k3是无量纲非线性扭转弹簧刚度，＝ωh／ωθ，ωh、ωθ为只有线性平移刚度或线性俯仰刚度的单自由度系统的固有频率，u＝V／bωθ，V为平均风速。

图1 二元机翼模型Fig.1 Sketch of the two－dimensional airfoil

本文研究在参激宽带实噪声作用下非线性系统的矩Lyapunov指数，而对于此非线性系统，本质上我们更关心界定系统概率1稳定边界的最大Lyapunov指数。根据Oseledec乘法遍历定理［7］可知，一个非线性系统的最大Lyapunov指数与其在平衡点邻域中的线性化系统的最大Lyapunov指数完全一致，因此在本文中，我们只研究这个非线性系统在其平衡点邻域内的线性化系统的矩Lyapunov指数。同时，在系统无量纲速度u中加入宽带噪声ξ（t），并假设系统的阻尼项ε2阶小量、随机项均为ε阶小量。

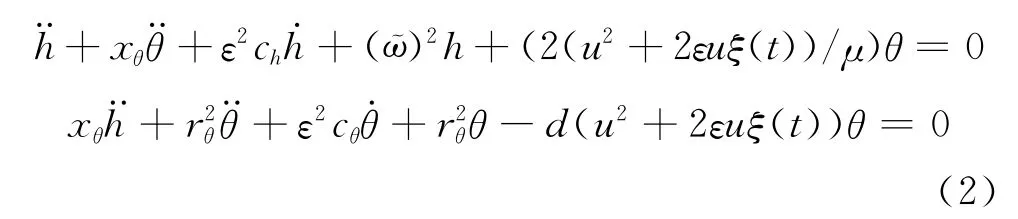
由于（εξ（t））2为更高阶小量，对系统基本没有影响，所以上式中未包含此项。通过进一步变换可以得到以下运动方程：

其中：

下面令系统阻尼和噪声均为零，得到以下派生系统

由式（5）解出系统固有频率为

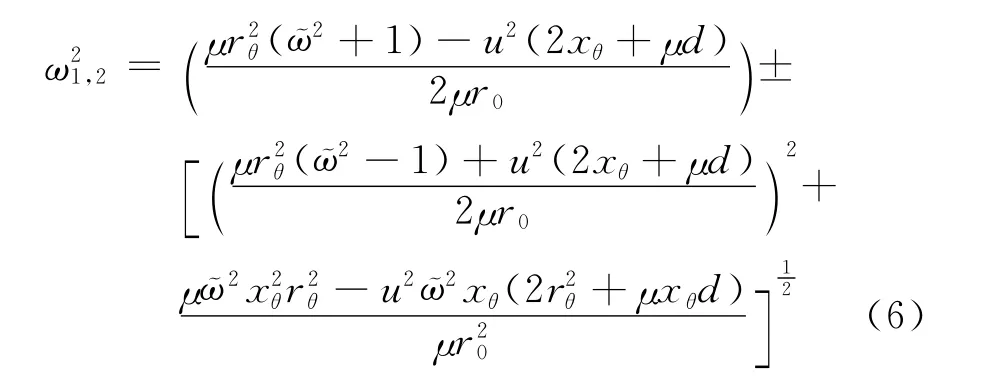
引进变换：

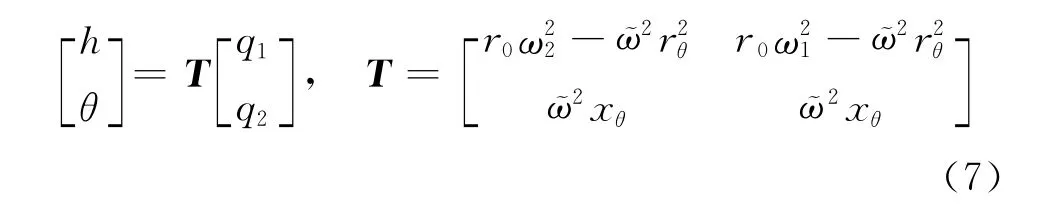
代入式（3），系统化成

代入各系数矩阵可得：

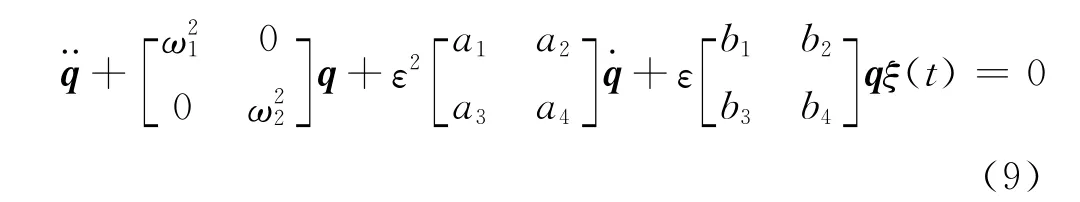
其中：

2 近似Markov过程

由于系统阻尼、噪声的sin和cos谱密度均为ε2阶无穷小量且ξ（t）为宽带噪声，因此可以对（9）式采用随机平均法得到系统的近似Itô随机微分方程。给出噪声ξ（t）的sin和cos功率谱密度分别为

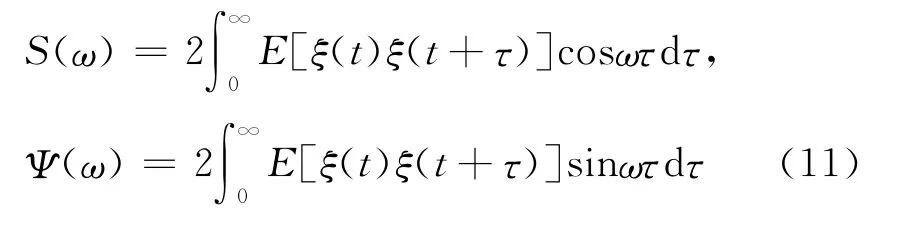
E［·］为期望算子。

通过引入如下变换：

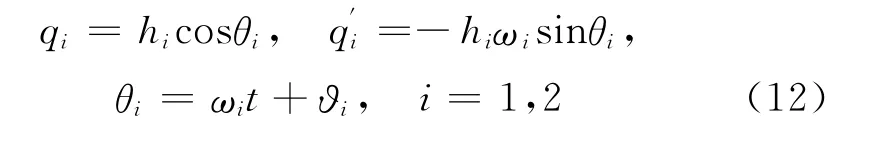
代入（9）式，即可得到关于h1，φ1，h2，φ2的四个一阶微分方程：

通过假设系统的固有频率ω1、ω2相差比较大，可以得到经过随机平均之后的振幅hi（t）和相位角ϑi（t）是解耦的。同时随着ε的减小，系统（13）的解弱收敛，并近似为一个扩散的Markov过程。下面对系统方程（13）采用随机平均法，得到It控制方程：

其中，Wh和Wϑ为两个相互独立的Wiener过程。此处采用随机平均法的主要目的就是让平均振幅过程hi（t）和相位角过程φi（t）解耦，从而对于系统方程（13）的研究就可以转化为对平均振幅hi（t）的研究，这样可以显著降低系统维数，减小问题的求解难度。

因此，下面只需给出系统（14）中第一个随机微分方程的系数表达式即可：

3 矩Lyapunov指数

令：＝rcosφ＝rsinφ，φ∈［0，］，由It微分公式可以得到关于变量r、φ的It随机微分方程：

其中：

由矩Lyapunov指数的定义可知：

同时，式（16）中第一个微分方程的解r（t；r0）的p次幂为：

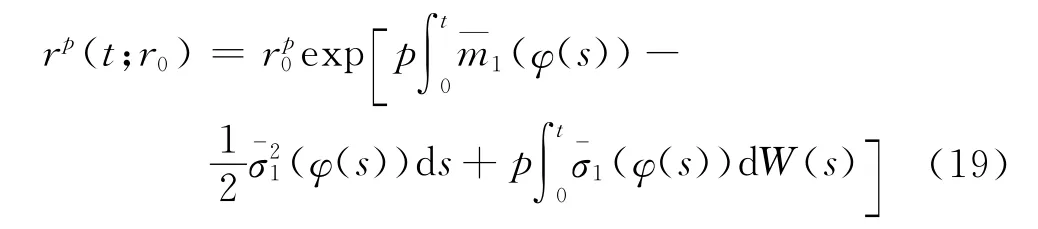
上式的期望为：

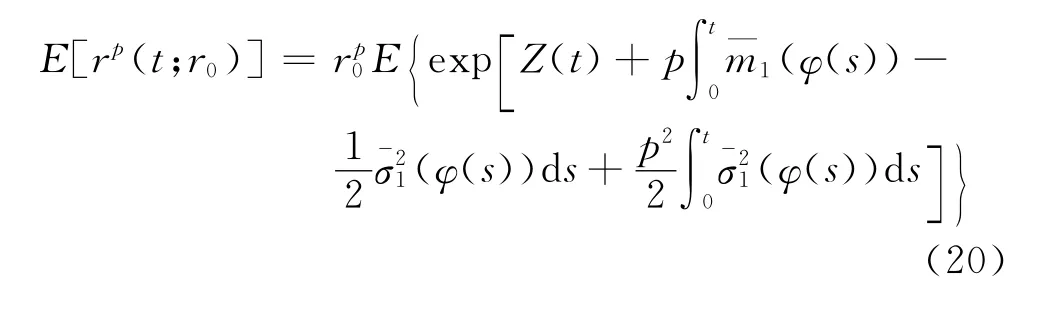
其中：

根据Girsanov定理，由式（20）可以得到：

其中：

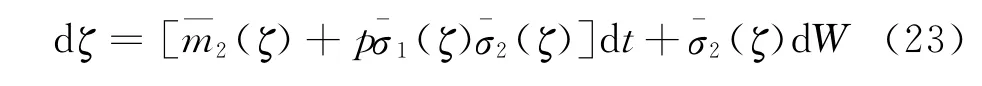
通过Feynmann－Kac公式将随机微分方程（16）的解的函数的期望E［rp（t）］＝f（ζ，p，t）转化为下列线性偏微分方程的解：

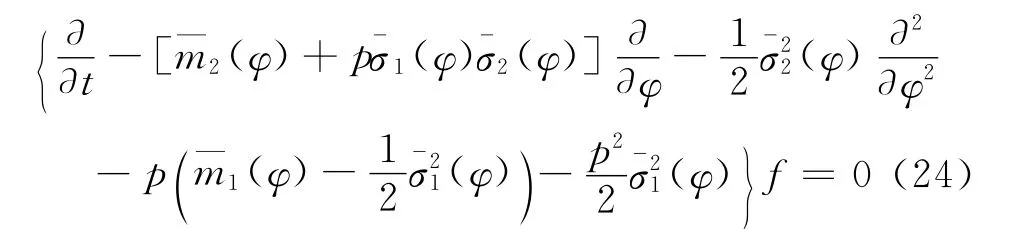
根据Arnold［7］可知，矩Lyapunov指数就是稳定算子的最大特征值，即：

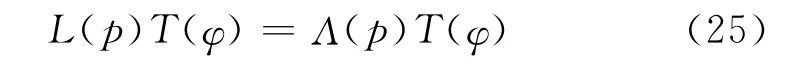
其中，稳定性算子为：

根据 Wedig［17］和 Bolotin［18］，T（φ）能 展 开 为 正 交Fourier余弦级数：

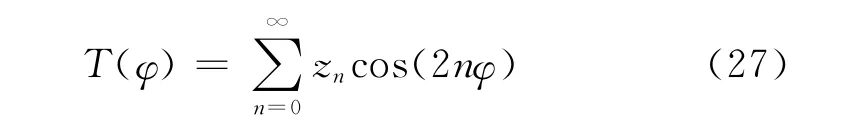
将式（27）代入式（25）并在两边同乘cos（2mφ）以后，对φ积分得到：

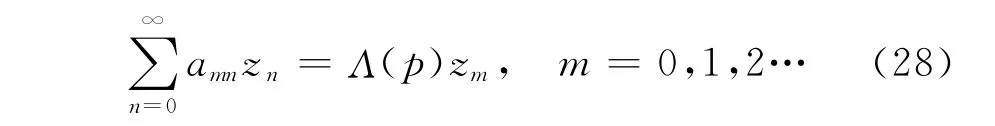
其中：

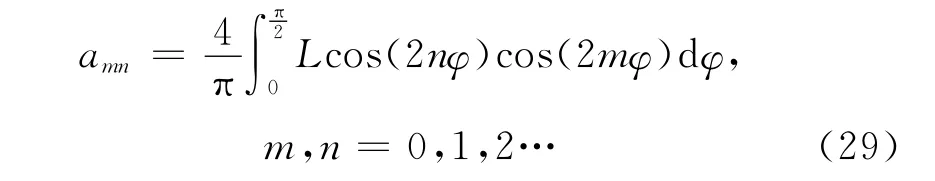
由上述元素构成的矩阵为：

若令Z＝［z0z1z2z3…zn…］T，则式（28）即可转化为：

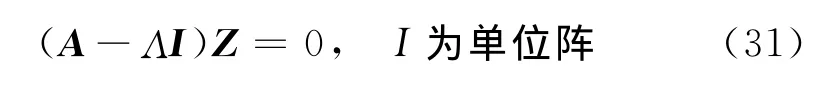
如果方程（31）关于Z存在非零解，那么它的系数行列式（A－ΛI）应该等于0。因此，求Λ（p）就转化为求矩阵A＝（amn）的无穷个子矩阵的特征值，这样得到了一个特征值的无穷序列，它的每一个元素都是Λ（p）的近似值。因此当n→∞时，通过这种方法求出的近似特征值序列应该收敛于Λ（p）的近似值的真实值，否则，就是不正确的。然而随着n的增加，计算量呈指数型增长，为此，我们用截断的方法，即取n为有限数，来获取Λ（p）的近似值。例如，当n＝0时，得到Λ（p）＝a00。当n＝1时，Λ（p）的近似值是A的二阶子矩阵的特征值。当n＝2时，Λ（p）的近似值是A的三阶子矩阵的特征值。由于矩阵A中元素的复杂性，我们仅仅列出A的三阶子矩阵中的元素的表达式。

其中，

4 数值验证

下面我们将通过对系统（9）采用Monte Carlo仿真，得到系统矩Lyapunov指数的数值解［19］，来验证近似解析解得可靠性。令x1＝q1，x2＝，x3＝q2，x4＝，系统（9）可化为：

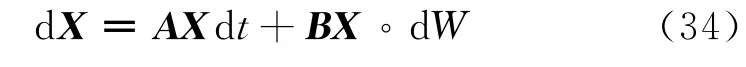
其中：

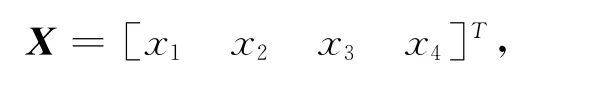
由于此处扩散矩阵的特殊性，Wong－Zakai修正项为零，所以Stratonovich方程的漂移项和Itô方程的漂移项是一致的。因此It方程为：

图2 矩Lyapunov指数近似解析解与数值解比较Fig.2 Comparison of the approximate analytical and numerical results of the moment Lyapunov exponent

5 讨 论

下面通过研究矩Lyapunov指数与系统各参数之间的关系，可以得到以下对工程实际具有指导价值的结论。

首先通过调整参数u，得到系统矩Lyapunov指数曲线随u增大不断向左移动，如图3所示，稳定性指标δp不断减小，这将直接影响系统矩稳定的区域；而随着u的增大，系统的最大Lyapunov指数也会由负变正，说明系统由几乎肯定稳定变为几乎肯定不稳定。根据参数u在上文中的表达式可知u主要由平均来流速度V所决定。也就是说，随着平均来流速度V的增大，系统的矩稳定性会随之降低；当V达到某临界值时，系统最大Lyapunov指数大于零，发生概率1意义失稳，出现颤振。这就是从随机的角度刻画了颤振发生的机理，因此我们可以从这个角度进一步研究系统各参数对随机颤振的影响。

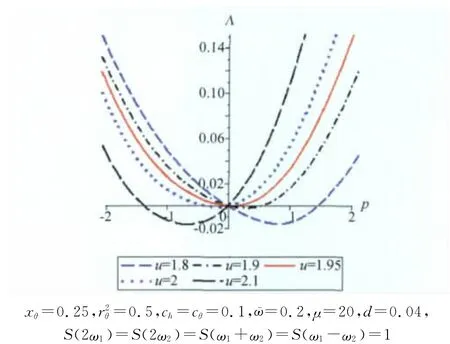
图3 参数u对矩Lyapunov指数的影响Fig.3 Effect of uon the moment Lyapunov exponent

其次，通过调整宽带噪声各频率cos谱密度，可以得到系统矩Lyapunov指数对随机噪声各频率谱密度的敏感性，如图4所示。由图可知，随着噪声2ω2、ω1＋ω2的cos谱密度的增加，系统的矩 Lyapunov指数曲线均重合在一起，未发生显著变化，如图4（b、c）所示，说明噪声的2ω2、ω1＋ω2的cos谱密度对系统的矩Lyapunov指数没有影响，因此在实际工程中可以不用关注随机噪声中2ω2、ω1＋ω2的cos谱密度的变化。而随着其余两个频率的cos谱密度的增加，系统矩Lyapunov指数曲线不断向左移动，表明稳定性指标δp不断减小，系统的矩稳定性区域不断向左移动；系统的最大Lyapunov指数也会由负变正，表明系统由几乎肯定稳定变为几乎肯定不稳定。但是，系统对这两个个频率的敏感性是不一样的。由图4（a、d）可知，系统矩Lyapunov指数曲线相对于宽带噪声2ω1的cos谱密度的变化幅度大于相对于宽带噪声ω1－ω2的cos谱密度的变化幅度，说明系统对宽带噪声2ω1的cos谱密度更为敏感。所以，在工程实际中一定要重点监测随机激励2ω1的cos谱密度变化，当然ω1－ω2的cos谱密度的变化也应适当关注。对于随机激励各频率的sin功率谱密度，由于在进行随机平均法的时，积分全部为零，因此可以不用关注各频率的sin功率谱密度的变化。

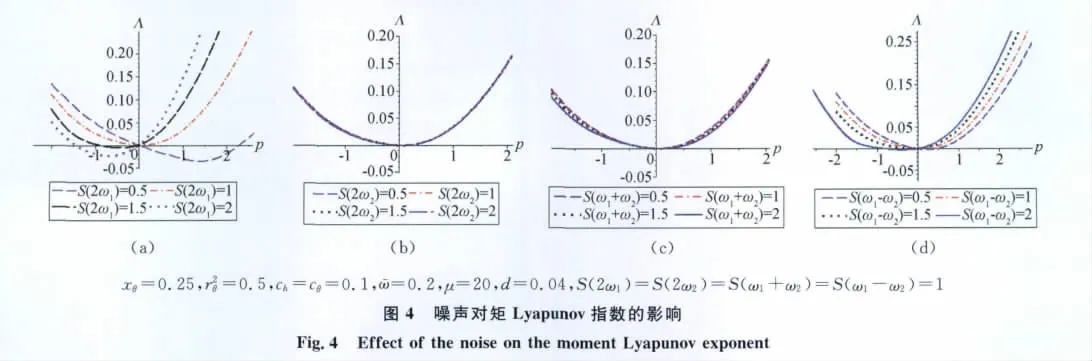
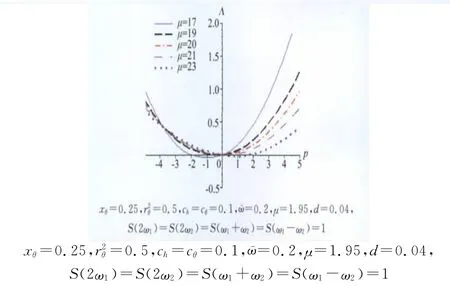
图5 无量纲质量μ对矩Lyapunov指数的影响Fig.5 Effect ofμon the moment Lyapunov exponent

然后，我们通过适当变动参数μ，得到无量纲质量μ对系统稳定性的影响。由图5可知，随着系统无量纲质量μ的增加，系统的稳定性不断增强。但是，在实际工程中，机翼的质量总是有限的，而且尽可能取小，因此会和我们此处的结论产生冲突。此时，我们可以进一步计算无量纲质量的增加或减小对系统临界速度的提高或降低的影响，根据这个影响的大小在适当的范围内确定最优无量纲质量。对最优无量纲质量的确定，本文不作进一步讨论。

最后，通过对参数d分析发现：随着d的增大，系统矩Lyapunov指数曲线逐渐向左移动，系统的矩稳定性指标δp不断减小，系统的矩稳定性不断降低，如图6所示。而参数d主要由弹性轴在半弦点后的距离与半弦长的比值a所决定。也就是说，随着弹性轴E不断向后移动，系统的矩稳定性不断降低。因此在实际设计中应考虑系统的弹性轴适当靠前。

图6 参数d对矩Lyapunov指数的影响Fig.6 Effect of don the moment Lyapunov exponent

7 结 论

本文主要研究了在随机宽带噪声作用下，机翼的矩Lyapunov指数的表达式及其相应的随机稳定性问题。通过对矩Lyapunov指数的表达式的研究，得出机翼颤振的矩Lyapunov稳定性主要由其参数u、μ、d以及随机激励各频率的cos谱密度所决定。进一步研究得到u、μ、d、S（2ω1）、S（ω1－ω2）等参数变化对系统矩Lyapunov指数的影响。以上结果表明，噪声对非线性系统的稳定性有着重要的影响，建议相关设计部门在进行可靠性分析时，除一般的强度分析以外，还应将噪声纳入考虑的范畴。

［1］FORSEHING H W，沈克扬译，管德校.气动弹性力学原理［M］.上海：上海科技文献出版社，1982.（FORSEHING HW，SHEN KY，GUAN D.Aeroelasticity theory［M］.Shanghai：Shanghai Scientific and technological Literature Publishing House，1982.）

［2］IBRAHIM R，ORONO P，MADABOOSI S.Stochastic flutter of a panel subjected to random in－plane forces.ITwo mode interaction［J］.AIAAJournal，1990，28（4）：694－702.

［3］IBRAHIM R，ORONO P.Stochastic nonlinear flutter of a panel subjected random in－plane forces［J］.InternationalJournalofNonlinearMechanics，1991，26（6）：867－883.

［4］POIREL D，PRICE S J.Random binary（coalescence）flutter of a two－dimensional linear airfoil［J］.Journal ofFluidsStructure，2003，18（1）：23－42.

［5］POIREL D，PRICE S J.Bifurcation characteristics of a two－dimensional structurally nonlinear airfoil in turbulent flow［J］.NonlinearDynamics，2007，48：423－435.

［6］朱位秋.非线性随机振动与控制［M］.北京：科学出版社，2003：280－281.（ZHU Wei－qiu.Nonlinear stochastic dynamics and control［M］.Beijing：Science Press，2003：280－281.）

［7］ARNOLD L.Random dynamical systems［M］.Springer，Berlin，1998.

［8］KOZIN F，SUGIMOTO S.Relations between sample and moment stability of linear stochastic differential equations.Proceedings of Conference on Stochastic Differential Equations and Applications.Academic Press，New York，1977：145－162.

［9］ARNOLD L，DOYLE M M，NAMACHCHIVAYA N S.Small noise expansion of moment Lyapunov exponents for two－dimensional systems［J］.DynamicsandStability ofSystems，1997，12（3）：187－211.

［10］NAMACHCHIVAYA N S，ROESSEL H J V，DOYLE M M.Moment Lyapunov exponent for two coupled oscillators driven by real noise［J］.SIAMJournalofAppliedMathematics，1996，56：1400－1423.

［11］KHASMINSKII R Z，MOSHCHUK N.Moment Lyapunov exponent and stability index for linear conservative system with small random perturbation［J］.SIAM JournalofAppliedMathematics，1998，58（1）：245－256.

［12］NAMACHCHIVAYA N S，ROESSEL H J V.Moment Lyapunov exponent and stochastic stability of two coupled oscillators driven by real noise［J］.JournalofAppliedMechanics，2001，68：903－914.

［13］XIE W C.Moment Lyapunov exponents of a two－dimensional system under real noise excitation［J］.JournalofSoundandVibration，2001，239（1）：139－155.

［14］LIU X B，LIEW K M.On the stability properties of a Van der Pol－Duffing oscillator that is driven by a real noise［J］.JournalofSoundandVibration，2005，285（1－2）：27－49.

［15］ZHAO L C，YANG Z C.Chaotic Motions of an airfoil with non－linear stiffness in incompressible flow ［J］.JournalofSoundandVibration，1990，138（2）：245－254.

［16］刘济科，赵令诚.不可压气流中二元机翼的分叉分析［J］.应用力学学报，1992，9（1）：37－43.（LIU J K，ZHAO L C.Bifurcation analysis of airfoils in incompressible flow［J］.ChineseJournalofApplied Mechanics，1992，9（1）：37－43.）

［17］WEDIG W.Lyapunov exponent of stochastic systems and related bifurcation problems.in：S.T.Ariaratnam，G.I.Schueller，I.Elishakoff（Eds.），Stochastic Structural Dynamics：Progress in Theory and Applications，Elsevier Applied Science，New York，1988：315－327.

［18］BOLOTIN V V.The dynamic stability of elastic system.Holded－Day，San Francisco，1964.

［19］XIE W C，HUANG Q H.On the Monte Carlo simulations of moment Lyapunov exponents［J］.SolidMechanicsandItsApplications，2006，140：627－636.