半刚性钢框架竖向跨间刚度计算

杜加清,　夏军武

(中国矿业大学 力学与建筑工程学院, 江苏 徐州 221116)



半刚性钢框架竖向跨间刚度计算

杜加清,夏军武

(中国矿业大学 力学与建筑工程学院, 江苏 徐州 221116)

根据半刚性连接梁单元的转动刚度和传递系数，利用集体分配原理和反弯点法，推导了半刚性连接钢框架的竖向跨间刚度计算公式。实例计算结果表明：在节点连接刚度由刚接变为铰接的过程中，竖向跨间刚度逐渐减小且呈非线性变化;当节点连接为铰接时，竖向跨间刚度为零。文中公式计算结果与sap 2000有限元分析软件的计算结果相近，验证了该计算方法的可靠性。

半刚性连接; 钢框架; 竖向跨间刚度

0　引　言

竖向跨间刚度多应用于结构不均匀沉降分析和地基、基础、上部结构三者共同作用的研究中。目前,国内外对框架结构的竖向变形的研究,多是从结构全局的角度计算其竖向剪切刚度或抗弯刚度,如1953年Meyerhof[1]推导出钢框架结构等效抗弯刚度近似计算公式;孙家乐等[2]推导了考虑相互作用的连分式等效刚度公式;夏军武等[3]提出了钢框架连续化假定后的剪切模型,并给出了约束刚度计算公式;孙澄潮等[4]进行了地基变形时钢框架结构竖向刚度的计算。实际上整个框架对基础沉降变形的约束最终归结于柱脚处的局部约束,即文中提出的竖向跨间刚度。考虑到钢框架梁柱实际的半刚性连接性能,笔者推导了半刚性钢框架竖向跨间刚度计算公式,为钢框架结构竖向变形研究提供了参考。

1　系数推导

半刚性钢框架在进行内力分析时,需要重新推导梁单元转角位移方程,从而得到其转动刚度和传递系数。图1是三参数拟合的半刚性节点弯矩—转角曲线,从图中可以看出,曲线呈非线性变化,但其初始刚度与初始割线刚度具有相同的侧初始转角。

图1　连接的初始割线刚度

为了便于理论分析,选取刚度恒定、长度为零的弹簧模拟梁柱节点的连接[5],函数表达式为M=Krθr,θr为相对转角,Kr为弹簧刚度，取初始割线刚度即有效刚度。假定梁线刚度与弹簧刚度相对比值α=2EI/LKr=2i/Kr,其中EI为梁抗弯刚度,L为梁的跨度,i为梁线刚度。利用结构力学的方法推导一端半刚性连接的转动刚度和传递系数,得一端铰接梁单元的转动刚度为S=6i/(3α+2),传递系数为零。

2　竖向跨间刚度

2.1假定条件

计算竖向跨间刚度和侧向层间刚度的区别在于,后者考虑楼层的刚性假定,而前者考虑柱的弯曲变形,故文中作如下假定:

(1)对于层数较少的多层钢框架可以假设柱长不变,每一层梁节点的竖向位移差都等于柱脚的竖向位移差。

(2)仅考虑与该柱相邻跨的梁和柱的影响,忽略远端梁和柱对该柱竖向沉降的约束,并且假定沉降发生时,钢框架无水平侧移,梁跨中为反弯点。

2.2刚度计算

以图2的三层等跨半刚性连接钢框架为例计算,柱线刚度均为ic,梁线刚度均为ib,@表示半刚性连接节点,梁线刚度与弹簧刚度比值均为α=2EI/LKr。

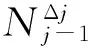
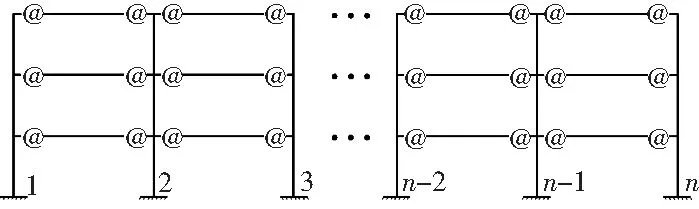
图2　多跨半刚性连接钢框架

图3　计算单元

利用结构力学方法,推导梁端部为半刚性连接时的转角位移方程,并得到梁两端产生相对位移差Δ时的梁端弯矩,即

对于边跨计算单元(图3a),根据假定条件,柱脚1处产生Δ1时,各层节点处的不平衡弯矩均为M,利用集体分配原理,即以二层节点作为不平衡弯矩集体分配点,将一层和三层节点的不平衡弯矩首先转移到二层节点后,再将所有的不平衡弯矩进行一次性集体分配和传递,最后得到各层节点处平衡弯矩及约束轴力:

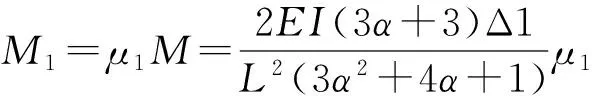
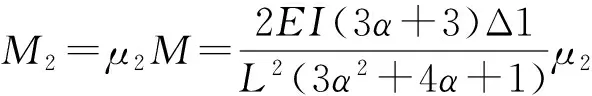
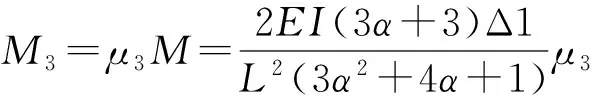
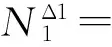
(1)

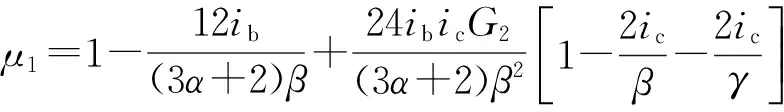
对于中间跨单元(图3b),柱脚j处产生Δj时,等跨钢框架各层节点处的不平衡弯矩为零(不等跨时不为零,需要应用集体分配原理),所以柱脚处的约束轴力为

(2)

根据式(1)和式(2),即可得到柱脚产生单位沉降时的跨间刚度:

3　应用实例

以图4所示的三层四跨半刚性连接钢框架为例,分别应用有限元分析软件sap 2000和上述公式进行钢框架竖向跨间刚度的计算。

图4　三层四跨半刚性连接钢框架

钢框架层高3 m,跨度6 m,柱截面H400 mm×400 mm×11 mm×18 mm,梁截面H500 mm×200 mm×9 mm×14 mm,取Δj和Δ1分别等于0.01 m,通过计算,分别得到边柱和中间柱的竖向跨间刚度K与α的关系曲线,如图5所示。

由图5可以看出,在节点连接刚度由刚接变为铰接的过程中,竖向跨间刚度逐渐减小且呈非线性变化,减小的趋势开始较为明显后逐步趋于平缓,当节点连接为铰接时即α趋于无穷大,竖向跨间刚度为零。

通过比较发现,边柱和中柱的公式计算结果均高于sap2000软件的计算结果。当α=0.5时,边柱的误差为4.2%,中柱的误差为11.1%,这表明梁跨中为反弯点的假定,过高的考虑了边柱中一侧梁柱及中柱中两侧梁柱的约束作用。随着节点刚度的减小,两者误差越来越小且趋于零,说明两者的计算结果趋于相等。

图5　钢框架竖向跨间刚度

4　结束语

考虑框架柱弯曲刚度的影响,通过理论分析推导了半刚性连接钢框架的竖向跨间刚度计算公式。实例分析得到了钢框架竖向跨间刚度在不同节点连接刚度下的变化规律,同时验证了文中计算方法的可靠性。真实框架半刚性节点连接可极大地削弱框架抵抗竖向不均匀沉降的能力,而传统的刚性框架假定过于放大了这种能力,故在结构不均匀沉降分析中获得了相对过于理想的结果,所以考虑真实节点的连接性能,对研究框架的竖向变形刚度及获得较精确的分析结果具有重要意义。

[1]MEYERHOF G G. Some recent foundation research and its appellation to design[J]. The Structural Engineer, 1953, 31 (6): 151-167.

[2]孙家乐, 武建勋. 考虑框架结构与地基基础相互作用的等效刚度公式研究[J]. 北京工业大学学报, 1986, 12(3): 57-67.

[3]夏军武, 袁迎曙, 董正筑. 采动区地基、条形基础与框架结构共同作用机理研究[J]. 岩土工程学报, 2007, 29(4): 537-541.

[4]孙澄潮, 刘刚君. 地基变形时框架结构竖向刚度的计算[J]. 建筑结构, 2010, 40(Z1): 65-68.

[5]胡习兵, 舒兴平, 沈蒲生. 半刚性连接钢框架的简化计算方法[J]. 湖南大学学报: 自然科学版, 2005(4): 18-23.

(编辑荀海鑫)

Vertical cross-inter stiffness calculation of semi-rigid steel frame

DUJiaqing,XIAJunwu

(School of Mechanics & Civil Engineering, China University of Mining & Technology, Xuzhou 221116, China)

This paper features the formula about vertical cross-inter stiffness of semi-rigid steel frame derived using mass distribution principle and anti-bend-point method and according to the rotation stiffness and transmission coefficient of beam element with semi-rigid connections. Calculation results show that changes of the stiffness from rigid joint to hinge joint results in a gradual decrease and a nonlinear change in vertical cross-inter stiffness and hinge joint gives zero vertical cross-stiffness. The similar calculation results derived from the formula and sap 2000 finite element analysis software verify the reliability of the calculation method.

semi-rigid connection; steel frame; vertical cross-inter stiffness

1671-0118(2012)02-0199-03

2012-02-19

杜加清(1987-),男,江苏省扬中人,硕士,研究方向:钢结构,E-mail:Jiaqingdu@163.com。

TU328

A