初中数学课后作业分层初探——作业创新、打造学生解题的4个层次

●

(南丰中学 江苏张家港 215628)

初中数学课后作业分层初探
——作业创新、打造学生解题的4个层次

●徐忠

(南丰中学 江苏张家港 215628)

在初中数学教学中，每天给学生布置适量的作业是深化知识、巩固知识、提高学生思考能力和检查学习效果的重要手段，也是复习与应用相结合的主要形式，是整个数学教学过程中的一个重要环节.然而在同一班级中，学生的数学学习能力、学习品质参差不齐，若按统一的要求布置作业，会造成尖子生吃不饱，学困生跟不上.长期以往，会造成尖子生得不到更好的提高，学困生对数学不感兴趣.基于以上原因，几年来笔者一直以“不同的学生在数学上得到不同的发展”为目标，对学生的作业进行创新和优化，即对学生的解题过程进行4个层次的训练，取得了不错的效果.

层次1每天布置适量的基础题和少量的中档题给全体学生练习，鼓励学生一题多解.

例如在学完平行四边形的判定定理后，布置了这样一道习题:

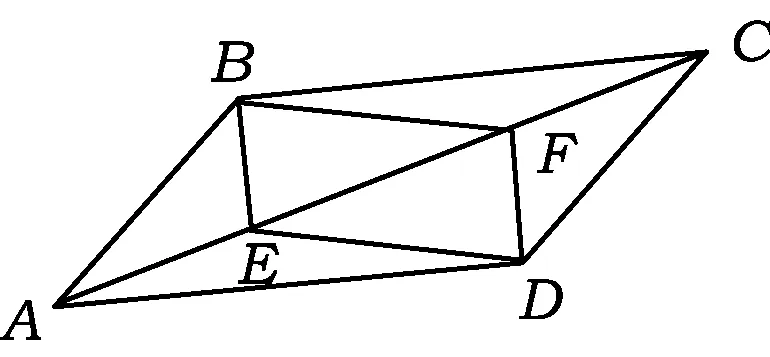
图1

习题1如图1所示，在ABCD中，点E，F都在对角线AC上，且AE=CF，联结DE，BE，DF，BF，则四边形DEBF是平行四边形吗？为什么？

笔者要求学生至少用2种以上的解法，并鼓励学生最好分别用平行四边形的4个判定定理解题.

反思让学生用多种方法解基础题，主要目的是让学生掌握概念和定理的基本应用,让学生在潜意识中比较这些方法的优劣，加深对它们的理解.在这个过程中不但巩固了上课内容，而且加强了知识之间的联系，开阔了视野，提高了学习兴趣，培养了学生的发散思维能力.

层次2在解完题目的基础上，选出一部分易错和概念易混淆的题目，要求全体学生写出解题过程中每一步所用的知识点，写出这些问题的来龙去脉以加深对题目和知识点的理解.

例如初学几何证明时，很多学生的证明思路不清晰，可要求学生在写证明时，写出每一步所用的知识点，巩固和加深对知识的理解.

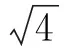
学生通过这些训练，对一些基本概念不再混淆.

反思基本概念和定理是解数学题的根本，很多学生做基础题时容易出错，难题做不出，其根本原因是基本概念和定理没有掌握好.通过这个层次的训练弥补了上一个层次的不足，夯实了学生的基础，为学生后续发展提供了必要的条件.

层次3通过题目中给出的信息，训练学生能够一眼发现解题方法的关键，并且能够针对题目提出一些问题，成为真正的解题高手.

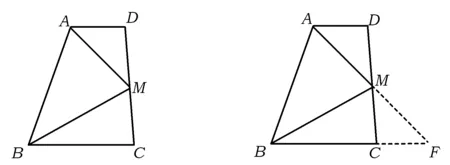
图2 图3

习题3如图2，已知在梯形ABCD中，AD∥BC，M是CD的中点，且AD+BC=AB，求证：AM，BM分别是∠DAB,∠ABC的角平分线.

有的学生在作业反思中写道：看到条件AD+BC=AB时，就马上想到要延长AM和BC，利用2个三角形全等把AD，BC这2条线段转化到一条线段上(如图3).同理也有学生想到延长AD和BM，方法同上.有的学生写到：看到条件AD+BC=AB时，马上想到可用中位线证明(如图4).

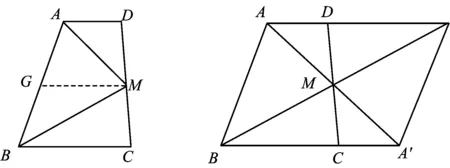
图4 图5

还有2个学生想到把梯形ABCD绕着点M旋转180°得到一个菱形来证明(如图5),可想到菱形的对角线平分一组对角这个定理.在提出的问题中，有的学生提出可以证明∠AMB=90°,有的提出可以证明S△ADM+S△BCM=S△ABM.还有学生提出当梯形ABCD是直角梯形(∠ABC=90°)时，△ABM是等腰直角三角形等问题.

反思达尔文的名言“最有价值的知识是方法的知识”，教师不仅要让学生学会知识，更要让学生学会和应用知识去思考和分析问题.通过这个层次的训练，让学生通过题目中给出的信息，采用分析法和综合法分析问题，找出解决问题的思路和方法，并根据题目的条件提出一些问题，这些都是教会学生学会学习、优化学习过程、提高学习效率的主要方法.

层次4能够理清题目的诸多变化，探究题目的数学思想方法，提高解决问题的能力，做题目的主人.

对于班内一些数学成绩优秀的学生，前面3个层次的训练远远不能够满足他们的需要，因此在教学中笔者有意识地让这些学生去研究题目，改编题目，探究题目的本质，真正成为题目的主人.

习题4如图6，在正方形ABCD中，边长AB=4，M是边AD上的一点，ME⊥AC，MF⊥BD，垂足分别是点E，F，那么ME+MF=________.

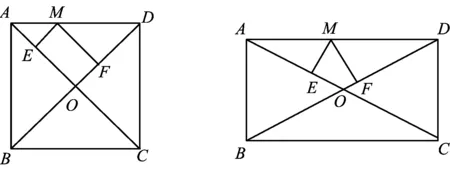
图6 图7

学生做完这道题目后进行了如下改编.

变式1如图6，在正方形ABCD中，边长AB=4，M是正方形ABCD边上的一个动点，ME⊥AC，MF⊥BD，垂足分别是点E，F，那么ME+MF=________.

变式2如图7，在矩形ABCD中，AB=3，AD=4，M是矩形ABCD边AD(或AB)上的一点，ME⊥AC，MF⊥BD，垂足分别是点E，F，那么ME+MF=________.

也有学生把变式2中的矩形换成菱形，换成平行四边形，发现这2条线段之和在变化，不是定值.因此有学生发现所求结果与等腰△AOD的面积和腰有关，于是有学生就进行了如下改编.

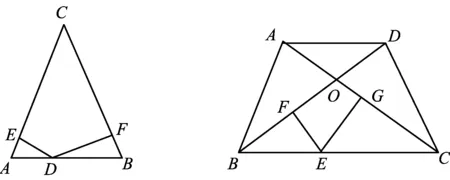
图8 图9

变式3如图8，在等腰△ABC中，BC=AC=5，AB=6，D是等腰△ABC底边AB上的任意一点，DE⊥AC，DF⊥BC，垂足分别是点E,F，那么DE+DF=________.

变式4如图9，在等腰梯形ABCD中，OB=OC=5，BC=6，E是等腰梯形ABCD底边BC上的任意一点，EF⊥BD，EG⊥AC，垂足分别是点F，G，那么EF+EG=________.

变式5如图10，在等腰梯形ABCD中，AB=CD=5，AD=3，BC=9，E是等腰梯形ABCD底边BC上的任意一点，EM⊥AB，EN⊥CD，垂足分别是点M，N，那么EM+EN=________.

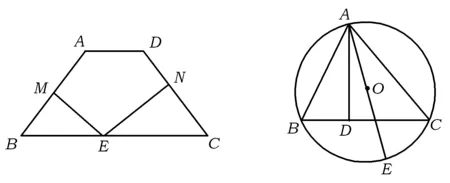
图10 图11

最后学生总结：这类动点题目的共同特点是都在等腰三角形或者等腰梯形中，都是用等积的思想解题.再如：

习题5如图11，△ABC是圆O的内接三角形，AD⊥BC于点D，AE是圆O的直径，求证：∠BAD=∠CAE.

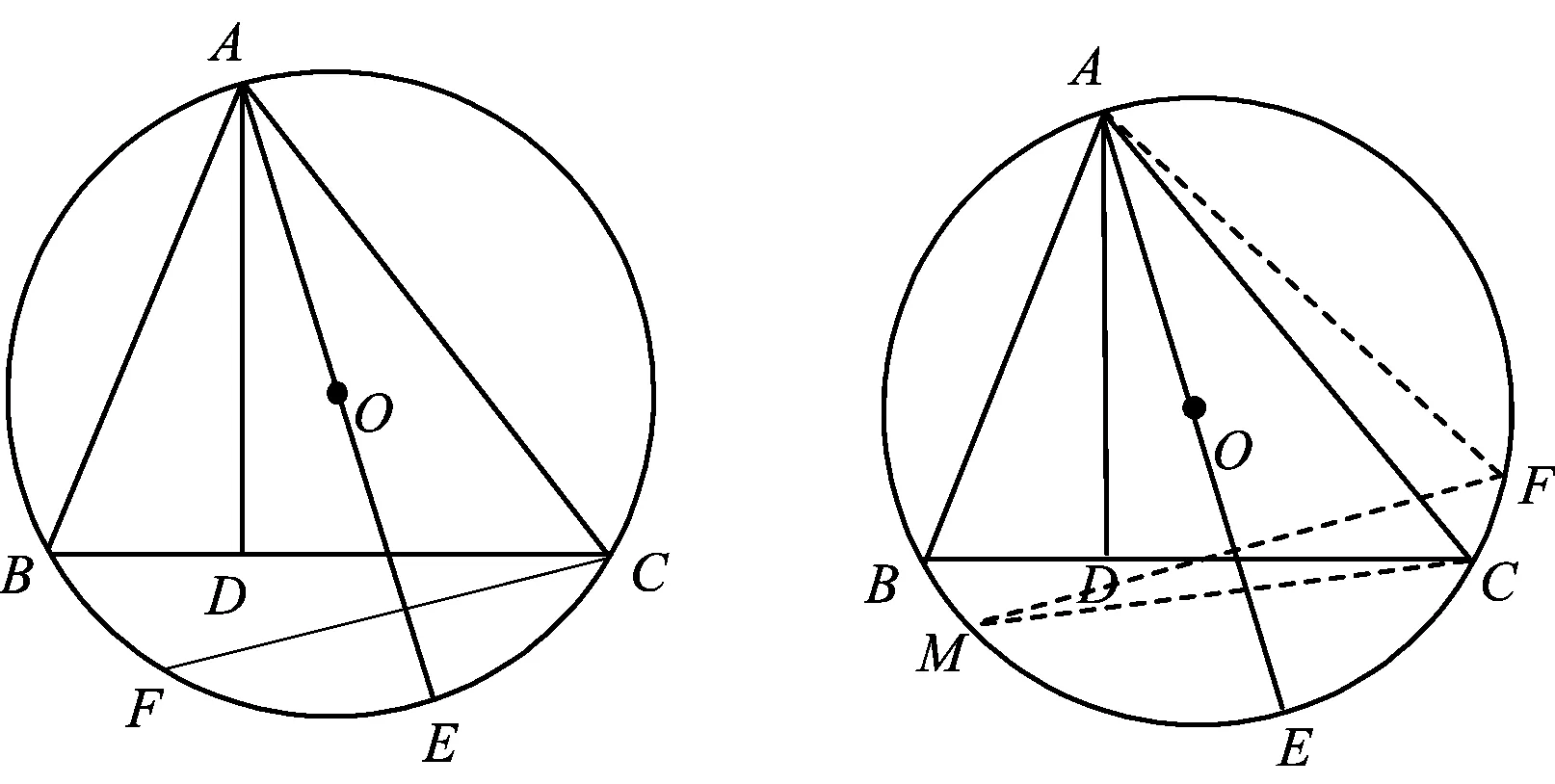
图12 图13

这道题目学生想出了很多解法，如联结BE或者CE，利用直径构造直角三角形解题;有学生发现，过点C作AE的垂线可以利用垂径定理解题，如图12,由垂径定理可知∠ACF=∠ABC，于是很容易得出∠BAD=∠CAE；又有学生发现过点B作AE的垂线也可以利用垂径定理解题；接着又有学生发现过点A，E作AE的垂线也可以解题.于是有学生大胆猜想：过直径AE上任意一点作垂线都能解题(如图13).因为∠BAD+∠ABC=90°，利用垂径定理知∠ABC=∠AFM+∠FMC，所以∠BAD+∠AFM+∠FAC=90°.又因为∠CAE+∠AFM+∠FAC=90°，所以∠BAD=∠CAE.学生通过探索总结出解题的关键和通法，对圆的知识掌握得就更深刻了(除了探索到通法外，还有其他解法就不一一列举了).

反思学生通过对这些题目的探索，用不同的思路、从不同的角度找出各种解题方法，然后总结方法，找到规律.还通过改编题目，理清题目的诸多变化，对题目进行大胆的猜想、有效的探索，激活了创新潜能，使自己不仅学到新知识，而且培养了实践能力和创新精神.

数学新课改的基本理念是“人人学有价值的数学，人人都能获得必需的数学，不同的人在数学上得到不同的发展”.对学生作业进行分层，使教师的着眼点面向了全体学生，使各类学生都有所学、有所用、有所提高，并且给每个学生创设了一个自主学习、自主钻研的舞台，促进了学生个性的发展.在层次1和层次2的练习中，主要目的是让每个学生掌握基础知识和基本技能，为后面2个层次服务.通过层次3和层次4的训练，让学生悟题、解题、研题，发散了学生的思维，在练习中让学生定位自己所在的层次，并且努力向更高的一个层次迈进，促使学困生向学良生转化、学良生向学优生转化，学优生则更优.在层次3和层次4的训练中，笔者把学生的研究成果、各种思考方法都贴在教室的问题角上，让每个学生进行交流、讨论，在合作中共同提高.

总之,对作业进行分层是因材施教的一种模式，体现了“绝不放弃每一个学生”和“不同的学生在数学上得到不同的发展”的教育思想，有利于每个学生的终身发展.