灰色Verhulst模型的优化及其应用

何 霞 王战伟

（郑州航空工业管理学院，郑州450015）

灰色Verhulst模型的优化及其应用

何 霞 王战伟

（郑州航空工业管理学院，郑州450015）

针对灰色Verhulst模型的优化单一，多种优化不能有效结合的情况，在同时优化背景值和初始值的基础上，建立将两种优化相结合的灰色Verhulst模型。利用该模型对我国手机网民增长规律进行研究，结果表明，优化灰色Verhulst模型具有较高的精度。

优化灰色Verhulst模型；背景值；初始值；手机网民

灰色系统理论中，灰色Verhulst模型在经济、管理等多个领域得到广泛应用，许多学者对该模型进行了深入的研究，不断地提高模型精度，扩大模型的适用范围,其中，文献[2]～[5]从以下几个方面对模型进行了优化：在参数估计和初始条件修正方面对灰色Verhulst模型进行了改进；通过改进灰导数优化了灰色Verhulst模型；优化了灰色Verhulst模型的背景值和结构参数，提高了模型的精度；建立了灰色离散Verhulst模型，加强了模型适应性；通过建立无偏Verhulst模型，消除了灰色Verhulst模型本身具有的偏差。文献［10］、［11］通过改进无偏灰色Verhulst模型的初始条件，优化了无偏灰色Verhulst模型。但上述这些优化方法都是在某个方面对模型进行的优化，没能将相互独立的多个方面的优化相结合，达到综合优化灰色Verhulst模型的目的。鉴于此，本文在同时优化背景值和初始值的基础上，建立将两种优化相结合的灰色Verhulst模型，并将该模型用于我国手机网民增长规律的研究，结果表明，优化灰色Verhulst模型具有较高的精度。

1 灰色Verhulst模型建模机理

定义1[1]设X(0)=(x(0)(1),x(0)(2),…,x(0)(n))为原始序列，X(1)=(x(1)(1),x(1)(2),…,x(1)(n))是X(0)的1-AGO序列，其中(n))为背景值序列，其中z(1)(k)=0.5(x(1)(k)+x(1)(k-1)),k= 2,3,…,n。称x(0)(k)+az(1)(k)=b(z(1)(k))2为灰色Verhulst模型。称为灰色Verhulst模型的白化方程。

定理1设X(0)=(x(0)(1),x(0)(2),…,x(0)(n))为原始序列，X(1)=(x(1)(1),x(1)(2),…,x(1)(n))是X(0)的1-AGO序列，其中为背景值序列，其中z(1)(k)=0.5(x(1)(k)+x(1)(k-1)),k=2,3,…,n。则

（1）灰色Verhulst模型的最小二乘估计参数序列满足

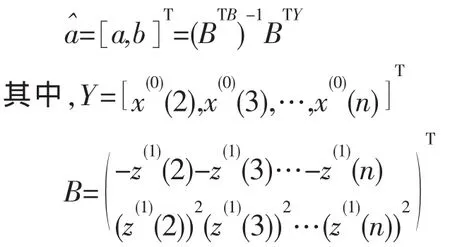
（3）灰色Verhulst模型的时间响应序列为

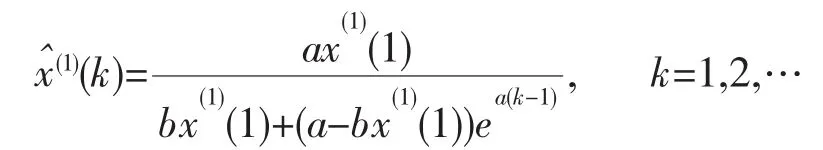
（4）还原值

2 灰色Verhulst模型的优化

由定理1可以看出，灰色Verhulst模型的拟合与预测精度不仅取决于参数a和b，而且受到初始值的影响，而定理2中将初值取为x(1)(1)并没有理论依据。为此，将初始值x(1)(1)取为x(1)(n)，既符合灰色系统理论新信息优先原理，同时又能提高模型的精度。同时，由文献［11］可知，背景值由z(1)(k)=0.5(x(1)(k)+x(1)

定理2设X(0)=(x(0)(1),x(0)(2),…,x(0)(n))为原始序列，X(1)=(x(1)(1),x(1)(2),…,x(1)(n))是X(0)的1-AGO序列，其中为背景值序列,其中k=2,3,…,n，初始值为x(1)(n)，则

（1）灰色Verhulst模型的最小二乘估计参数序列满足

（3）灰色Verhulst模型的时间响应序列为

（4）还原值

证明：只需将背景值由z(1)(k)=0.5(x(1)(k)+x(1)(k-1))换为，将初始值由x(1)(1)换为x(1)(n)，其余证明与定理1相同。

3 优化灰色Verhulst模型的应用

根据中国互联网络信息中心发布的《中国互联网络发展状况统计报告》，截至2010年6月，我国网民数量达到4.2亿人，较2009年底增加3 600万人。截至2010年6月达2.77亿，半年新增手机网民4 334万人，增幅高达18.6%。为了更好地了解我国手机网民数量增长的规律和发展趋势，利用本文建立的优化灰色Verhulst模型对我国手机网民增长进行研究。

3.1 手机网民数据收集

根据我国互联网络信息中心发布的统计报告，我们从中收集了自2006年6月到2010年6月每半年调查统计一次的手机网民人数（表1）。

表1 我国2006～2010年手机网民数量

取2006年6月到2009年12月的数据作为原始数据序列，而把2010年6月的数据用来检验模型预测精度。于是,我们建立手机网民增长的优化灰色Verhuslt模型。

3.2 模型的建立与求解

设手机网民数量序列

则累计手机网民数量序列

背景值序列

由定理3可得到模型参数:

于是,灰色Verhulst模型的白化方程为

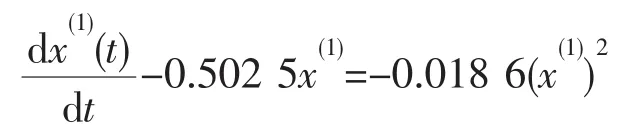
其时间响应函数为

从而得到X(1)的模拟值与预测值为

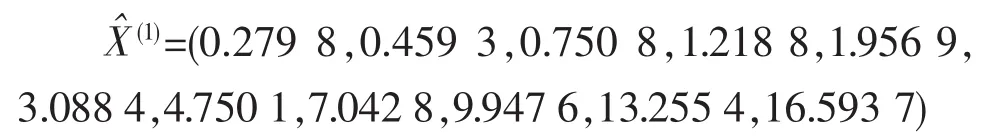
还原求出X(0)的模拟值与预测值为

3.3 模型精度对比分析

为了更好地进行比较，根据表1中的数据，求出定理1中的传统灰色Verhulst模型的响应函数为

从而可以求出相应的模型值。现将传统灰色Verhulst模型的模拟预测值与本文中的优化灰色Verhulst模型的模拟预测值进行对比（表2）。

从表2可以看出，传统灰色Verhulst模型的模拟平均相对误差为50.01%，而本文中优化灰色Verhulst模型的模拟平均相对误差仅为8.23%，精度远远高于传统灰色Verhulst模型。

表2 传统与优化模型的模拟与预测误差对比表

4 结论

本文在优化背景值和初始值的情况下，建立了一种优化灰色Verhulst模型，并应用该模型建立了我国手机网民数量的灰色Verhulst模型，精度对比结果显示该优化灰色Verhulst模型比传统灰色Verhulst模型具有更高的精度。

[1]邓聚龙.灰色系统理论教程[M].武汉:华中理工大学出版社，1990.

[2]何文章,吴爱弟.估计Verhulst模型中参数的线性规划方法及应用[J].系统工程理论与实践，2006，26(8):141-144.

[3]党耀国,刘思峰,刘斌.以x^(n)为初始条件的GM模型[J].中国管理科学，2005,13(1):132-135.

[4]刘威,徐伟.灰色Verhulst模型参数估计的一种新算法[J].计算机仿真，2008，25(11):119-123.

[5]陈露,张凌霜.基于初值修正的组合灰色Verhulst模型[J].数学的实践与认识，2010，40(11):160-164.

[6]王正新,党耀国,沈春光.灰色Verhulst模型的灰导数改进研究[J].统计与信息论坛，2010，25(6):19-22.

[7]戴文战,熊伟,杨爱萍.灰色Verhulst模型的改进及其应用[J].化工学报，2010，61(8):2097-2100.

[8]崔立志,刘思峰,李致平.灰色离散Verhulst模型[J].系统工程与电子技术，2011，33(3):590-593.

[9]王正新,党耀国,刘思峰.无偏灰色Verhulst模型及其应用[J].系统工程理论与实践，2009，29(10):138-144.

[10]沈春光,陈万明,裴玲玲.无偏灰色Verhulst模型初始条件的优化[J].统计与信息论坛，2011，26(5):3-6.

[11]沈春光,陈万明,裴玲玲.无偏灰色Verhulst模型的优化及其应用[J].内蒙古师范大学学报：自然科学汉文版，2011，40(4):325-328.

[12]骆公志，崔杰，谢乃明.灰色GM(1,1)模型新的改进方法[J].统计与决策，2008（22）：11-13.

Optim ization of Grey Verhulst M odel and Its App lication

HE Xia WANG Zhanwei
(Zhengzhou Institute of Aeronautical Industry Management,Zhengzhou 450015)

According to the fact that there exists simple optim ization method and types of optim ization w ithout effective combination.By optim izing simultaneously background values and initial values,we build an optim ized grey Verhulstmodel.Based on themodel,we research Chinesemobile internet-user grow th.The result indicates that the optim ized grey Verhulstmodel can achieve more satisfactory precision than traditional grey Verhulst model.

optim ized grey Verhulstmodel；background value；initialvalue；mobile internet-user

TP122

A

1673-1980（2012）03-0173-04

2011-12-14

河南省教育厅科学技术研究重点项目（12B110027）；河南省哲学社会科学规划项目(2011BJJ021)；郑州航空工业管理学院青年科研基金项目（2011113001，2011113003）

何霞（1976-），女，河南周口人，硕士，讲师，研究方向为应用数学、灰色系统理论。