基于连通支配树的异构传感器网络拓扑修复算法

史庭俊，方旭明，杨云

(扬州大学 信息工程学院，江苏 扬州 225009)

1 引言

无线传感器网络(WSN, wireless sensor networks)是大量微型传感器节点自组形成的多跳通信网络。目前，无线传感器网络已被广泛应用于军事、安全监视、生态环境监测、医疗健康等领域[1]。因为应用于不同领域的传感器节点在感测能力、计算能力、通信能力和能量存储等方面存在着差异，所以由不同类型传感器节点组成的网络称为异构传感器网络(heterogeneous sensor networks)[2]。相对于由相同类型传感器节点组成的同构传感器网络(homogeneous sensor networks)，异构传感器网络是一种更加实际的网络模型[3]。

设计无线传感器网络算法的重要目标之一是降低网络运行时的能量消耗从而延长网络的生命周期[4]。拓扑控制(TC, topology control)算法是一种减少无线传感器网络能量消耗的常用方法。拓扑控制是指在保证网络连通和覆盖所有节点的前提下，使大量的节点进入休眠状态以节省能量，只使用少量节点来转发数据。目前，在无线传感器网络的研究中通常使用连通支配集(CDS, connected dominating sets)理论来实现这种拓扑控制[5]。然而，无论是在同构传感器网络中求解极小连通支配集[6]，还是在异构传感器网络中求解极小连通支配集都被证明是一个NP-hard问题[7]。

由于传感器节点电池的能量总是有限的且不易被补充，因此节点失效后会导致无线传感器网络的拓扑结构发生改变。为了使网络保持连通和覆盖所有节点的特性，本文提出了一种基于连通支配树的异构传感器网络拓扑修复(HSNTR, heterogeneous sensor network topology restoration)算法。该算法的主要优点如下。

1) 与集中式执行的算法相比，HSNTR算法采用分布式方式执行，只需使用一跳邻节点列表而无需知道节点的位置信息，因此它具有更好的扩展性。

2) 与分布式执行的算法相比，HSNTR算法使用更小的消息和时间复杂度，因此它具有更好的能效性。

3) 与使用同构传感器网络模型的算法相比，HSNTR算法使用异构传感器网络模型，因此它具有更好的实用性。

与使用静态全局修复方式的算法相比，HSNTR算法使用动态局部修复方式使连通支配树恢复连通和覆盖所有节点，因此它具有更好的可靠性。

2 相关工作

在同构传感器网络环境下构造连通支配集的算法主要分成2类。第一类算法分为2个阶段执行。算法首先在第一个阶段构造一个极大独立集，然后在第二个阶段选择连接节点将极大独立集连成一个连通支配集。其中代表性的算法主要有文献[8]提出的一种基于准全局信息的生成树算法、文献[9]提出的一种基于节点度的分布式算法和文献[10]提出的一种能量高效的 EECDS(energy efficient connected dominating set)算法。第二类算法也分为2个阶段执行。算法首先在第一个阶段生成一个未经优化的连通支配集，然后在第二个阶段使用修剪规则去掉冗余的节点以使连通支配集变得更小。其中代表性的算法主要有文献[11]提出的一种基于多点中继的分布式算法、文献[12]提出的一种基于递归的极小连通支配集算法和文献[13]提出的一种基于修剪规则的 CDS-Rule-K(connected dominating set under rule k)算法。

EECDS算法在第一个阶段使用染色法构造一个极大独立集。初始时，所有的节点均为白色节点。算法选择一个白色节点染成黑色并且广播黑色消息。当白色邻节点收到黑色消息时，它被染成灰色并且广播灰色消息。当白色邻节点收到灰色消息时，它广播查询消息以获取邻节点的状态与优先级，同时它还设置一个定时器。如果在定时器超时前没有收到任何邻节点的黑色消息，那么它将染成黑色并且广播黑色消息，否则它将保持白色。当所有的白色节点都被染成灰色或黑色时，第一个阶段执行结束，其中所有的黑色节点构成一个极大独立集。算法在第二个阶段使用贪婪方式选择连接节点将极大独立集连成一个连通支配集。算法选择一个非独立节点染成蓝色并且广播蓝色消息。当独立节点收到蓝色消息时，它被染成蓝色并且广播邀请消息。当非独立节点收到邀请消息时，它将计算优先级并且广播更新消息。算法选择优先级最大的非独立节点染成蓝色并且广播蓝色消息。当所有的黑色节点都被染成蓝色时，第二个阶段执行结束，其中所有的蓝色节点构成一个连通支配集。

CDS-Rule-K算法在第一个阶段使用标记法来构造一棵没有优化的连通支配树。初始时，所有的节点广播 Hello消息以形成邻节点列表并且相互交换列表。如果一个节点的邻节点没有被其他节点所覆盖，那么它将被标记成连通支配树的一个节点。算法在第二个阶段使用修剪规则去掉树中冗余的叶子节点。直到所有冗余的叶子节点都被去掉之后，算法才会得到一棵优化的连通支配树。

DLEDSR(dynamic local energy and DSR based repair)算法是一种基于同构传感器网络模型的拓扑修复算法[14]。当一个节点的能量低于算法规定的最小能量阈值时，它将向所有休眠的邻节点广播唤醒消息，以使它们进入复苏状态，同时这些复苏节点也会向邻节点广播唤醒消息。当失效节点复苏邻节点的子节点收到唤醒消息时，它们会向其子节点广播唤醒消息，以使它们进入复苏状态。当失效节点复苏邻节点的父节点收到唤醒消息时，它们会向其子节点和父节点广播唤醒消息，以使它们进入复苏状态。当失效节点复苏邻节点的祖父节点收到唤醒消息时，它们会向其子节点广播唤醒消息，以使它们进入复苏状态。当算法的广播周期结束时，所有距离失效节点的两跳子节点和三跳父节点都已处于复苏状态。由于该算法在修复网络拓扑的过程中发送大量消息会产生通信拥塞和能量浪费，因此它不适合运行于规模很大、能量有限的无线传感器网络环境。

3 相关概念与网络模型

定义1 若图G为简单连通图，当且仅当图G同时满足以下条件：1) 任意1个节点没有环；2) 任意2个节点之间至少存在1条通路。

定义2 设图G为简单连通图，所有节点的通信半径r∈[rmin, rmax]，如果两个节点u,v之间的距离不大于min(ru, rv)时，那么节点u和节点v之间就存在一条边，称图G为双向圆图。其中，rmin是所有节点中最小的通信半径，rmax是所有节点中最大的通信半径，min( )是求解最小值的函数。

定义 3 设图 G=(V,E)为双向圆图，如果节点u, v∈V且(u, v)∈E，即节点u和节点v在图G中存在一条边，那么称节点u和节点v是相邻节点。其中，V表示顶点集，E表示边集。

定义4 设图G=(V,E)为双向圆图，如果节点集U⊆V且∀u, v∈U⇒(u, v)∉E，即U中的任意2个节点互不相邻，那么称节点集U为图G的独立集，称节点集U中的节点为独立节点。如果∀u∈(VU) ⇒U∪{u}不再是一个独立集，那么称节点集U为图G的极大独立集。其中，V表示顶点集，E表示边集。

定义5 设图G=(V,E)为双向圆图，如果节点集 D⊆V 且∀u∈(V－D)⇒(∃v∈D∧(u,v)∈E)，即不在D中的任一节点至少与D中一个节点相邻，那么称节点集D为图G的支配集。如果图G能由节点集D导出一个连通子图，那么称节点集D为图G的连通支配集。其中，V表示顶点集，E表示边集。

定义 6 设图 G=(V,E)为双向圆图，VT⊆V，ET⊆E，如果 T=(VT,ET)是图 G由节点集 VT导出的一棵生成树，并且节点集VT是图G的连通支配集，那么称T为图G的连通支配树。其中，V表示顶点集，E表示边集。

在异构传感器网络模型中，网络拓扑使用双向圆图来表示，其中实线表示节点之间的通信链路，虚线表示节点的通信半径，如图1所示。

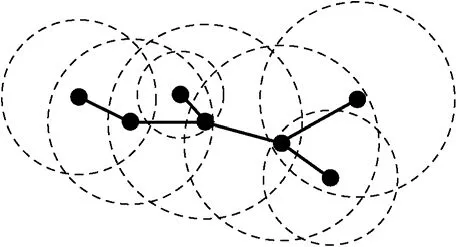
图1 异构传感器网络模型

异构传感器网络模型具有如下性质。

1) 网络在完成部署以后所有的节点会自组地形成一个多跳通信网络。

2) 网络中的节点可以具有不同的通信半径和初始能量。

3) 网络中的所有节点都有一个全向天线以使它们的通信区域呈现圆形。

4) 网络中能通信的节点之间的距离必定不超过它们的通信半径。

4 HSNTR算法

4.1 选择标准

算法优先选择剩余能量多、通信半径大的节点成为骨干节点。每个节点的优先级不是通过排序运算得到的，而是通过在每个节点设置一个定时器来实现的。算法将节点的优先级设置成定时器的倒数，这样定时器的值越小就代表节点的优先级越大，如式(1)所示。

其中，Tu表示节点u定时器的值，Tcon表示一个的时间常量。a和b分别表示剩余能量和通信半径的权重因子。根据不同网络的应用需求，可以通过改变权重因子来配置网络。如果a大于b，那么骨干节点的剩余能量会更多，否则骨干节点的通信半径会更大。Eu表示节点u的剩余能量，Einit表示节点的初始能量。Ru表示节点u当前使用的通信半径，Rmax表示节点可以使用的最大通信半径。

4.2 执行流程

算法首先在第一个阶段使用染色法、标记法和生成树技术构造一棵连通支配树，同时使用修剪规则去掉树中冗余的叶子节点，然后在第二个阶段修复因节点失效而拓扑改变的连通支配树。修剪规则的定义是如果一个节点的所有邻节点已被它的所有兄弟节点覆盖，那么该节点就是一个冗余的叶子节点。算法规定，如果未标记的白色节点第一次收到应答消息，那么它将被标记为应答节点的子节点。

阶段1（构造连通支配树）

步骤 1 算法初始化时，网络中所有的节点都是未标记的白色节点，如图2所示。

图2 步骤1执行后的示例

步骤 2 算法首先选择一个白色节点作为连通支配树的根节点，然后这个节点被标记为黑色节点，并且广播黑色消息，如图3所示。

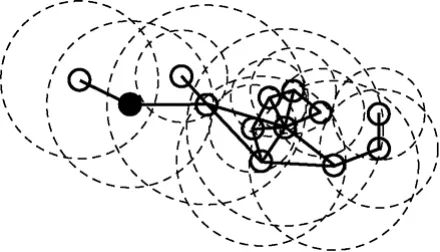
图3 步骤2执行后的示例

步骤 3 当未标记的白色节点收到黑色应答消息时，它将被标记为灰色节点，并且广播灰色消息，如图4所示。

图4 步骤3执行后的示例

步骤 4 当未标记的白色节点收到灰色应答消息时，它将根据优先级的计算公式设置定时器的值。如果它在定时结束前收到来自兄弟节点的黑色消息，那么它将被标记为灰色节点，并且广播灰色消息，否则它将被标记为黑色节点，并且广播黑色消息，如图5所示。

图5 步骤4执行后的示例

步骤 5 当灰色节点收到来自子节点的黑色消息时，它将被标记为黑色节点，并且广播黑色消息，如图6所示。

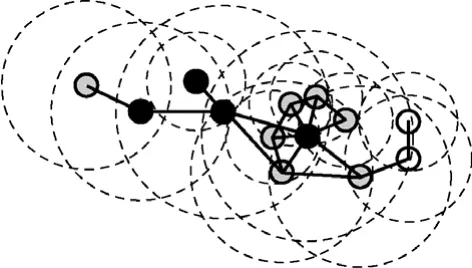
图6 步骤5执行后的示例

步骤 6 当黑色节点没有任何一个子节点时，它将被标记为灰色节点，并且广播灰色消息，如图7所示。

图7 步骤6执行后的示例

步骤 7 当所有的白色节点都被标记为灰色或黑色节点时，算法的阶段1执行结束。其中，所有的黑色节点构成一棵连通支配树，如图8所示。

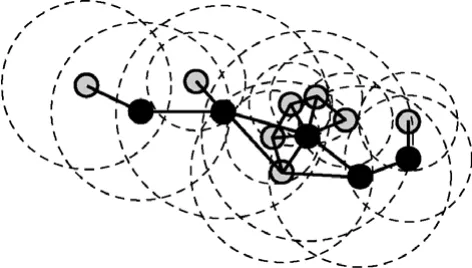
图8 步骤7执行后的示例

阶段2（修复连通支配树）

步骤 1 当黑色节点失效时，它将广播唤醒消息。所有的灰色邻节点被标记为深灰色节点，并且广播深灰色消息，如图9所示。

图9 步骤1执行后的示例

步骤2 当深灰色节点收到2个不能连通的黑色节点广播的消息时，它将代替失效节点成为这 2个黑色节点的父节点和子节点，同时它被标记为黑色节点，并且广播黑色消息，如图10所示。

图10 步骤2执行后的示例

步骤3 当深灰色节点收到2个不能连通的黑色和深灰色节点广播的消息时，它将成为黑色节点的子节点和深灰色节点的父节点，同时它被标记为黑色节点，并且广播黑色消息，如图11所示。

图11 步骤3执行后的示例

步骤4 当深灰色节点收到2个不能连通的深灰色节点广播的消息时，它将成为已经有父节点的节点的子节点和还没有父节点的节点的父节点，同时它被标记为黑色节点，并且广播黑色消息，如图12所示。

图12 步骤4执行后的示例

步骤5 当深灰色节点没有任何一个子节点时，它将被标记为灰色节点，并且广播灰色消息，如图13所示。

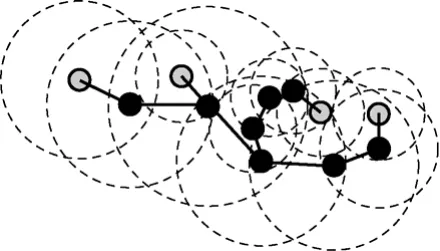
图13 步骤5执行后的示例

步骤 6 当所有的深灰色节点都被标记为灰色或黑色节点时，算法的阶段2执行结束。其中，所有的黑色节点构成一棵新的连通支配树。

4.3 实现代价

由于网络中的每个节点在执行HSNTR算法时至多广播6条消息，因此，有n个节点的网络至多广播 6n条消息，即 HSNTR算法的消息复杂度为O(n)。又由于 HSNTR算法在每个节点运行的时间复杂度为O(1)，因此，HSNTR算法在有n个节点的网络中运行的时间复杂度为O(n)。

5 理论分析

5.1 相关定理

定理1 节点v1和节点v2是节点u在双向圆图中的2个相邻节点，如果d(u,v1)≤d(u,v2)且d(v1,v2)≤d(u,v1)，那么节点v1和节点v2也是相邻节点。其中，d( )是求解2个节点之间距离的函数。

证明 因为节点v1是节点u在双向圆图中的相邻节点，所以节点v1的通信半径rv1≥d(u,v1)。同理，节点v2的通信半径rv2≥d(u,v2)。又因为d(v1,v2)≤d(u,v1)且 d(u,v1)≤d(u,v2)，所以 d(v1,v2)≤rv1且 d(v1,v2)≤rv2，即节点v1和节点v2在双向圆图中是相邻节点。

定理2 在双向圆图中，任一节点至多相邻 N个独立节点。

证明 设任一节点u至多相邻N个独立节点，当节点u所有的独立节点都趋向于两两相邻时，N将接近于最大极限。

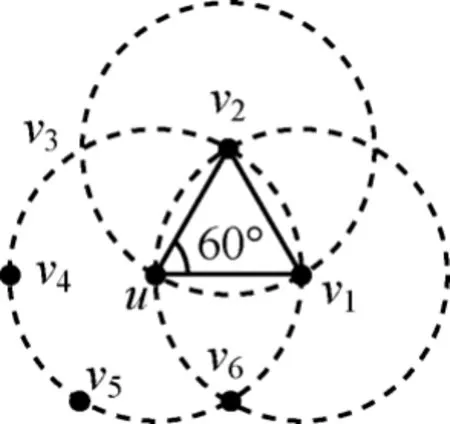
图14 k=1时的相邻节点分布

当k=1时，假设v1,…,v6分别是与节点u相邻的独立节点，如图 1所示。因为三角形 v1uv2是等边三角形，所以 d(u,v1)=d(u,v2)=d(v1,v2)。由定理 1可知，节点v1和节点v2是相邻节点，与它们是独立节点相矛盾，所以节点u至多相邻5个独立节点，如图15所示。

图15 k=1时的独立节点分布

当k＞1时，假设v1,…,vj分别是与节点u相邻的独立节点，如图16所示。

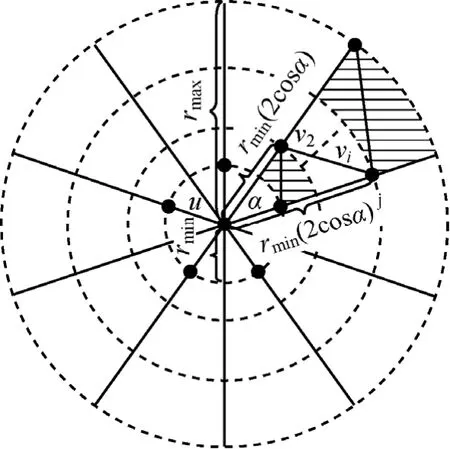
图16 k＞1时的相邻区域分布

因为d(u,v1)=d(v1,v2)且∠v1uv2=α，所以d(u,v2)=rmin×2×cosα。同理可得，第j个节点与节点u的距离d(u,vj)=rmin×(2×cosα)j。又因为rmin(2×cosα)j≤rmax，所以由定理1可知，节点u在以α为弧度的扇形区域中至多存在 j个独立节点。又因为整个圆形区域至多被划分成个扇形区域，所以节点u在整个圆形区域内至多存在个独立节点。令，其中，k是一个大于 1的常数，。当时，f(α)取得极值所以节点 u至多相邻个独立节点。

定理 3 在双向圆图中，任何一个极大独立集中的节点个数都不超过N×|MCDS|。

证明 设I是双向圆图的极大独立集，MCDS是双向圆图的极小连通支配集。由定理2可知，在双向圆图中，任一节点至多相邻N个独立节点，因此极大独立集中的节点个数至多是极小连通支配集中的节点个数的N倍，即|I|≤N×|MCDS|。

5.2 阶段1分析

性质1 在 HSNTR算法中，由白色直接染成黑色的节点集是极大独立集。

证明 设I是算法中由白色直接染成黑色的节点集，即不包括由灰色染成黑色的连接节点。因为算法中的白色节点都是按照灰色与黑色交替的方式染色的，所以黑色节点都是不相邻节点，即I是独立集。又因为任一灰色节点至少有一个黑色相邻节点，所以如果任一灰色节点被染成黑色，那么 I将不再是独立集，即I是极大独立集。

性质2 由HSNTR算法生成的树是连通支配树。

证明 算法从根节点开始广播消息，让所有的节点构成一棵生成树。由性质1可知，算法构造了一个极大独立集。因为在双向圆图中，极大独立集也是支配集[1]，所以算法构造了一个支配集。又因为树是连通的，所以算法构造了一棵连通支配树。

性质3 由 HSNTR算法选择的连接节点至少相邻2个独立节点。

证明 在算法中，独立节点的所有白色邻节点都被标记为灰色节点。当灰色节点存在一个独立的子节点时，它将被标记为黑色节点，即它被选为连接节点。因此，由算法选择的连接节点至少相邻 2个独立节点。

性质 4 由 HSNTR算法选择的连接节点不超过N×|MCDS|-1。

证明 设I是由算法构造的极大独立集，C是由算法选择的连接节点集，T是由算法生成的连通支配树。由性质3可知，任一连接节点至少相邻2个独立节点，因此当T中的所有节点排成一条直线时连接节点达到最多，即|C|=|I|-1。由定理3可知，|I|≤N×|MCDS|，因此|C|≤N×|MCDS|-1。

性质5 由 HSNTR算法生成的连通支配树中的节点不超过2N×|MCDS|-1。

证明 由性质1和定理3可知，由算法构造的极大独立集中的节点不超过 N×|MCDS|。由性质 4可知，由算法选择的连接节点不超过N×|MCDS|-1。由性质2可知，由算法生成的树是连通支配树，因此由算法生成的连通支配树中的节点不超过2×N×|MCDS|-1。

5.3 阶段2分析

性质 6 由HSNTR算法修复的树仍是连通支配树。

证明 算法首先唤醒失效节点的所有休眠的邻节点，然后利用它们将所有无法连通的节点重新连通，并且重新指派它们的父节点和子节点。因为所有唤醒的黑色节点恢复了树的连通性，同时确保每个休眠的灰色节点至少与一个黑色节点相邻，所以由算法修复的树仍然是一棵连通支配树。

性质 7 由HSNTR算法修复的连通支配树至多增加M个节点。

证明 当k=1时，由定理2可知，失效节点u至多使用6个扇形区域中的节点就能连通所有邻节点，如图17所示。

图17 k=1时的连接节点分布

因为在同一个扇形区域内的所有节点都相邻，所以每个扇形区域内至多使用2个节点就能连通其他区域。又因为所有增加的连接节点可以形成一个环，所以最后2个扇形区域分别只需使用一个节点就能与其他的区域连通。由此可见，当k=1时，算法至多使用10个节点就能修复连通支配树。

因为在同一个弧形区域内的所有节点都相邻，所以每个弧形区域内至多使用2个节点就能连通其他区域。又因为所有增加的连接节点可以形成一个环，所以10个半径为rmin的扇形区域分别只需使用一个节点就能与其他的区域连通。由此可见，当k＞1时，算法至多使用个节点就能修复连通支配树。

图18 k＞1时的连接节点分布

6 仿真分析

本文使用一种面向无线传感器网络的拓扑控制仿真工具Atarraya对不同算法进行了性能仿真。仿真假设无线传感器网络中所有的节点都被均匀地散布在一个200m×200m的正方形区域内，并且每个节点的最大通信半径为50m。为了观察不同算法之间的性能差异，仿真中的节点总数分别取为20、40、60、80和 100。仿真首先在不同的节点总数处分别生成 50种网络拓扑结构，然后在每种网络拓扑结构处重复执行3次算法，最后将平均值作为仿真的最终结果。如果随机生成的网络拓扑结构不是连通的，那么仿真将重新生成一个新的网络拓扑结构，直到这个网络拓扑结构连通为止。对算法性能的仿真分析如下所述：

1) 能效性分析

如图 19所示，虽然不同的算法在不同的节点总数处构造骨干网时消耗的能量都在增大，但是HSNTR算法比其他算法消耗的能量要小得多，这表明HSNTR算法的能量使用效率要更加高效。

图19 消耗能量随节点总数变化的曲线

2) 扩展性分析

如图 20所示，虽然不同的算法在不同的节点总数处构造骨干网时发送的消息总数都在增多，但是HSNTR算法比其他算法发送的消息总数要少得多，并且还呈现出了非常缓慢地线性增长趋势，这表明HSNTR算法更能满足无线传感器网络规模不断扩大拓展的应用需求。

图20 发送消息随节点总数变化的曲线

3) 可靠性分析

如图 21所示，不同的算法在不同的节点总数处保持网络连通和覆盖所有节点的时间都在变长，但是HSNTR算法比其他算法保持网络运行的时间要长，这表明HSNTR算法能够在节点失效的情况下使得网络更加可靠地运行。

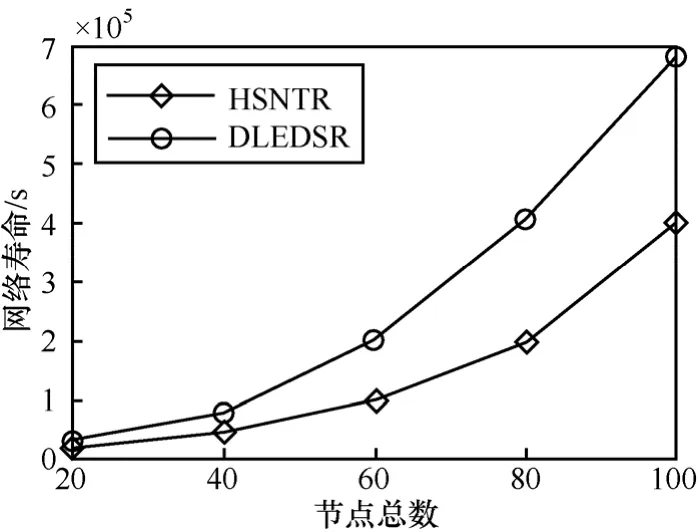
图21 网络寿命随节点总数变化的曲线

7 结束语

本文在异构传感器网络模型的基础上提出了一种基于连通支配树的拓扑修复算法。由于算法使用定时器对竞争骨干的节点进行排序，因此节点避免了排序算法从而减少了大量的计算能耗。又由于算法只要发送很少的消息就能构造和修复虚拟骨干网，因此节点避免了网络风暴从而减少了大量的通信能耗。本文分析了算法在构造和修复骨干网的过程中具有的一些性质。最后，仿真显示出算法在能效性、扩展性和可靠性方面的优越性。由于移动的节点可能使得网络不再连通，因此下一步的工作是利用图论中的支配吸收集理论和有向圆图对移动传感器网络的拓扑控制算法进行研究。

[1] 孙利民, 李建中, 陈渝. 无线传感器网络[M]. 北京: 清华大学出版社, 2005.SUN L M, LI J Z, CHUN Y. Wireless Sensor Networks[M]. Beijing:Tsinghua University Press, 2005.

[2] DUARTEMELO E J, LIU M Y. Analysis of energy consumption and lifetime of heterogeneous wireless sensor networks[A]. Proc of the GLOBECOM 2002[C]. New York, USA, 2002. 21-25.

[3] YARVIS M, KUSHALNAGAR N, SINGH H, et al. Exploiting heterogeneity in sensor networks[A]. 24th Annual Joint Conference of the IEEE Computer and Communications Societies(INFOCOM 2005)[C].2005. 878-890.

[4] CHANG J H, TASSIULAS L. Maximum lifetime routing in wireless sensor networks[J]. IEEE/ACM Transactions on Networking, 2004,12(4):609-619.

[5] 解文斌, 李佳, 鲜明等. 基于拓扑特性的分布式虚拟骨干网算法[J].软件学报, 2010, 21(6):1416-1425.XIE W B, LI J, XIAN M, et al. Distributed virtue backbone network algorithm based on topology characteristic[J]. Journal of Software,2010, 21(6):1416-1425.

[6] CLACK B N, COLBOURN C J, JOHNSON D S. Unit disk graphs[J].Discrete Mathematics, 1990, 86(13):165-177.

[7] GAREY M R, JOHNSON D S. Computers and Intractability: a guide to the Theory of NP-completeness[M]. New York: Freeman, 1979.

[8] WAN P L, ALZOUBI K M, FRIEDER O. Distributed construction of connected dominating set in wireless ad hoc networks[J]. ACM/ Kluwer Mobile Networks and Applications(MONET), 2004, 6(2): 141-149.

[9] CHENG X, DING M, DU D H, et al. Virtual backbone construction in multihop ad hoc wireless networks[J]. Wireless Communications and Mobile Computing, 2006, 6(2):183-190.

[10] YUAN Y Z, JIA X, YAN X H. Energy efficient distributed connected dominating sets construction in wireless sensor networks[A]. Proceedings of the 2006 ACM International Conference on Communica-tions and Mobile Computing[C]. New York, USA, 2006. 797-802.

[11] WU L, LOU W, DAI F. Extended multipoint relays to determine connected dominating sets in MANETs[J]. IEEE Transactions on Computers, 2006, 55(3):334-347.

[12] BUTENKO S, MURPHEY R, PARDALOS P M. Recent Developments in Cooperative Control and Optimization[M]. Berlin: Springer,2003.

[13] WU J, CARDEI M, DAI F, et al. Extended dominating set and its applications in ad hoc networks using cooperative communication[J].IEEE Transactions on Parallel and Distributed Systems, 2006, 17(8):851-864.

[14] LABRADOR M A, WIGHTMAN P M. Topology Control in Wireless Sensor Networks: with a Companion Simulation Tool for Teaching and Research[M]. Berlin:Springer, 2009.

[15] RAEI H, SARRAM M, ADIBNIYA F, et al. Optimal distributed algorithm for minimum connected dominating sets in wireless sensor networks[A]. Proceedings of the 5th IEEE Int’l Conf on Mobile Ad Hoc and Sensor Systems[C]. Atlanta, GA, 2008. 695-700.