多用户MIMO系统中基于单天线功率约束的功率分配方法

韩圣千，杨晨阳

（北京航空航天大学 电子信息工程学院，北京100191）

1 引言

在多用户多输入多输出（MU-MIMO, multiuser multiple-input multiple-output）系统中，脏纸编码（DPC）是能够实现广播信道容量的最优预编码[1]。但是由于DPC需要进行复杂的矢量编码，且通常要求很大的编码长度，因此具有很高的计算复杂度[2]。迫零（ZF, zero forcing）预编码是一种被广泛应用的次优MU-MIMO发射方案，能够以很低的计算复杂度消除多用户之间的干扰[3～5]。当系统的总用户数很大时，文献[6]的研究结果表明，基于多天线总发射功率受限（SPC, sum power constraints）的ZF预编码可以渐近达到 DPC的性能。文献[7]进一步证明了当考虑单天线功率约束（PAPC, per-antenna power constraints）时，ZF预编码仍然可以达到渐近最优的性能。

在无线通信系统中，考虑PAPC比SPC更具有实际意义[4,5,7,8]。一方面，由于在实际系统中每个天线的射频链路均存在独立的功率放大器，因此每个天线的发射功率都独立地受限于各自功率放大器的线性区间。另一方面，PAPC是未来通信系统的重要特征。分布式天线技术和多基站协作技术是未来无线通信系统保证蜂窝小区均匀覆盖的重要候选技术[4,5]。对于在地理位置上散布的多个天线和多个基站，它们的发射功率不可能互相共享，因此这2种技术是单天线功率约束的典型应用场景。

为了保证ZF预编码满足一定的发射功率约束，系统需要基于ZF波束形成矩阵对多用户进行功率分配。基于 SPC，最优功率分配具有灌水（waterfilling）结构，并且只包含一个水平面变量。文献[7]研究了基于PAPC的功率分配方法，指出以最大化多用户和数据率为准则的功率分配问题是一个凸优化问题，可以通过多种优化方法进行数值求解（例如内点法[9]），但是其计算复杂度随着变量维数的增加而快速增长。为了降低功率分配的复杂度，文献[10]提出了一种启发式方法。它首先假设基于PAPC的功率分配仍具有单水平面的灌水结构，然后通过适当地选择水平面变量以保证所有的天线均满足PAPC。文献[11]提出了更简单的等功率分配方法（EPA, equal power allocation），并指出在最大化多用户的最小数据率准则下 EPA是最优的功率分配方案。与最优的功率分配方法相比，启发式方法和EPA有效地降低了计算复杂度，但是其性能与最优性能之间存在较大的差距。

本文基于ZF预编码，以最大化多用户和数据率为准则，提出一种新的低复杂度功率分配方法。首先证明基于PAPC的最优功率分配仍具有灌水结构，但是包含多个水平面变量；然后提出一种次优方法来获得这些水平面变量。仿真结果表明，所提出方法的性能优于现有的启发式方法和EPA，能够以较低的计算复杂度获得接近最优功率分配的性能。

本文所采用的数学符号定义如下：黑体大写、黑体小写和正常小写字母分别表示矩阵、行向量和标量，(· )T和 (· )H分别表示对矩阵或向量进行转置和共轭转置，I表示单位矩阵，1表示全 1向量，diag()x表示以向量x为对角元素的对角矩阵。

2 系统模型

考虑一个下行链路多用户MIMO系统，其中装有M个天线的基站通过空分复用方式服务K个单天线用户。对于 ZF预编码，用户k的波束形成向量 gk需要满足

其中，hj是用户j的下行信道向量，其维数为1×M。满足式(1)的ZF预编码并不唯一，其中比较常用的是基于信道矩阵伪逆的ZF预编码。由此，用户k的接收信噪比和可达数据率分别为

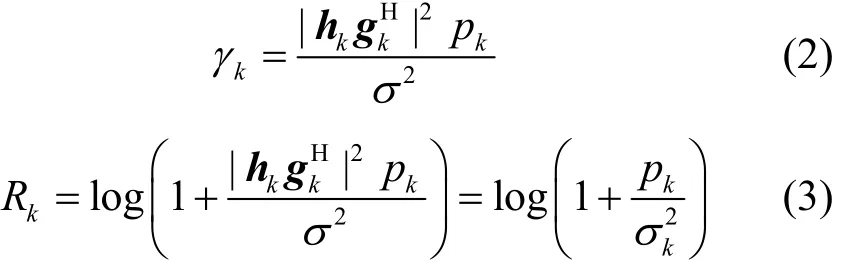
其中，pk是基站分配给用户k的发射功率，σ2是用户端的加性白高斯噪声的方差，

定义基站端的发射波束形成矩阵和功率分配矩阵分别为 G = [ g1H, … ,gKH]和 P = diag(p)，其中，p= [ p , …,p ]，则基站端的发射预编码为W = GP1。

21K定义矩阵G的第m行第k列元素为 gmk，可得基站端第m个天线的发射功率为

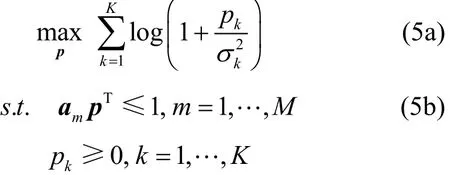
3 最优多水平面灌水功率分配

式(5)给出的功率分配问题是由凸目标函数和线性约束构成的凸问题，其拉格朗日方程可以表示为

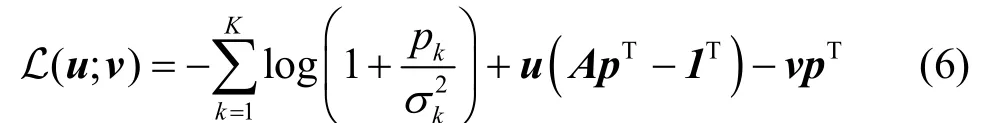
其中， u = [ u1,… ,uM]和v= [ v1, … ,vK]是对偶变量，其第m行第k列元素为 a 。mk

最优的p、u和v应满足以下KKT条件：

式(12)可以重新表示为

联合式(7)、式(9)、式(11)和式(13)，不难得到最优功率分配具有以下灌水结构：

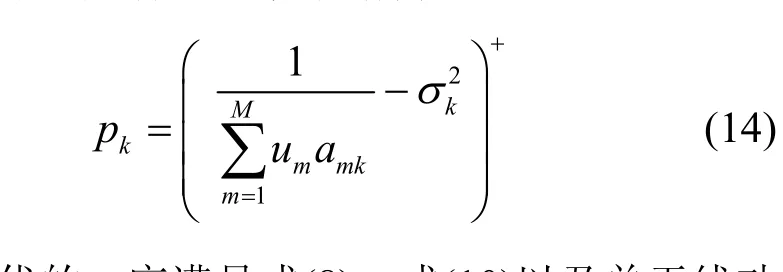
其中，最优的u应满足式(8)、式(10)以及单天线功率约束(5b)，(x)+= m ax(x, 0)。

由式(14)可以看出，最优的功率分配中包含由向量u决定的多个水平面。文献[12]研究了存在多个水平面的灌水功率分配问题，并且在 pk只与 uk有关的特定情况下，给出了计算u的有效方法。然而，不难看出，在式(14)中 pk由u中的所有元素共同决定，因此文献[12]给出的方法不能应用于本文所考虑的问题。

下一节将提出一种求解水平面变量u的次优方法。为此，首先通过下述定理给出该变量最优值的一些性质。

定理 1 对于如下的单水平面灌水功率分配优化问题

其中，λ需要满足：

由于优化问题(5)是凸问题且满足强对偶条件[9]，因此为了证明是优化问题(5)的最优解，只需证明满足优化问题(5)对应的KKT条件。通过比较式(14)和式(16)，不难发现当时，式(14)给出的 pk与式(16)给出的相同。因此，只需证明满足式(8)、式(10)以及单天线功率约束(5b)即可完成证明。

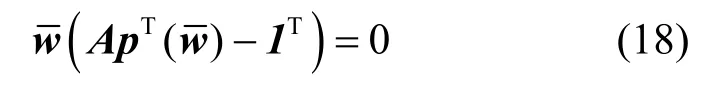
其中，引入了水平面变量λ以便于后述证明。由于λ＞ 0 ，因此它不影响式(19)的成立。

考虑到um=λ和pk= pk，可知式(10)也成立。由此，该定理得证。

4 低复杂度功率分配

根据上一节的定理，可以将计算最优水平面变量u转换为找出在优化问题(15)中满足 ampT(w ) ≤ 1的w， m = 1,… ,M 。根据式(19)并考虑和wm≥ 0 ，不难得出对于任意w，至少存在一个ampT(w ) = 1。因此，最优的w可以通过求解以下优化问题而得到

其中， qm(w ) = ampT(w ) -1。

然而，对优化问题(20)直接进行求解仍然比较困难。下面提出一种针对优化问题(20)的次优求解方法，它能够以较低的复杂度达到接近最优的性能。为此，考虑w在功率分配中的物理意义。在优化问题(15)中，w将原优化问题(5)中针对每个天线的功率约束转变为一个加权和功率约束，其中 wm体现了第m个天线的功率约束在加权和功率约束中的重要程度。不难看出，当 wm=1时，优化问题(15)的最优解一定能够使第m个天线的功率约束得以满足，即 qm= 0 。基于这一观察，所提出的次优方法迭代地选择不能满足功率约束的天线，并适当调整它们的加权参数，直至满足一定的迭代停止条件。

首先讨论加权向量w的迭代更新方法。设 wi-1和Si= [ s1, … ,si]分别表示第i次迭代中使用的加权向量和已选的不满足发射功率约束的天线序号组合。基于 wi-1，希望更新之后的 wi能够使 Si中天线的最大发射功率达到最小。根据以上对w的物理意义的分析，采用下面的次优更新方法

其中，0≤μ≤1，si表示第i次迭代中所选天线的序号， wi,m表示 wi的第m个元素。

式(21)给出的更新方法具有3个特征。一方面，只要 wi-1满足则有；另一方具有更大的权值，从而降低发射功率；最后，当qsi(wi)≥ 0时，可以证明qsi(wi) 是μ的单调递增函数（证明过程见附录）。

基于式(21)的特征，可以采用下面给出的二分法选择μ，使得天线 si在所有已选天线 Si中不再具有最大的发射功率。

1) 定义μmin=0和μmax=1。wi；由式(16)计算 p (wi) 和 qm( wi) ， m ∈Si。=μ；否则，更新μmin=μ。

4) 重复步骤 2)和 3)，直至 μmax-μmin＜ϵ，其中，ϵ是特定的门限值。

根据以上分析，所提出的低复杂度功率分配方法可以总结如下。

1) 初始化。设i=0，S0=φ（空集），T0={1,，即所有天线具有相同的权值，并计算 qm(w0)， m ∈ { 1,… ,M }。

2) 迭代。

① 设 i = i+ 1 ，从 Ti-1中选择具有最大发射功率的天线：，更新

② 根据式(21)更新 wi，其中对μ的计算分为2种情况：

当 i = 1 时，由于已选天线的个数为 1并且qsi(wi) 是μ的单调递增函数，因此μ的最优值为0，

当 i ＞ 1 时，μ可以通过上面给出的二分法得到。

③ 计算 qm( wi) ， m = 1,… ,M ，并定义 qSi=

3) 若 qTi＞qSi，重复步骤 2)；否则，由式(16)计算 p (wi) ，并得到最终的功率分配结果为

这里采用所有天线的最大发射功率maxm的p一定满足单天线功率约束。

5 仿真分析

本节通过蒙特卡洛仿真评估所提出功率分配方法的性能和复杂度。为了进行性能和复杂度比较，仿真中还考虑了其他 3种功率分配方法，包括最优功率分配、启发式功率分配[10]和等功率分配[11]，其中采用内点发[9]计算最优功率分配，并适当地配置内点法的参数使其在不降低性能的前提下具有尽可能低的计算复杂度。

设基站的总发射功率为P，每个天线具有相同的发射功率约束 P /M，信噪比定义为 P /σ2，仿真中设置为5dB。假设不同用户的信道相互统计独立，且每个用户的信道为统计独立同分布的瑞利衰落信道，由零均值单位方差的复高斯随机变量构成。假设基站已知所有用户的准确信道信息，并采用基于信道矩阵伪逆的ZF预编码服务多个用户。所有仿真进行1 000次蒙特卡洛实验。

图1给出了不同用户数K下4种功率分配方法的和数据率。可以看出，对于不同的用户数，所提出的低复杂度功率分配方法均能够获得接近最优功率分配的性能。等功率分配性能最差，并且与所提出的功率分配方法之间的差距随着被服务用户数的增长而扩大。启发式方法能够在一定程度上提高等功率分配的性能，但与所提出的功率分配方法相比仍有明显的性能差距。

图1 不同用户数K下4种功率分配方法的和数据率（基站天线数8M=，所提出方法的门限0.01=ϵ）

图2 比较了4种功率分配方法的计算复杂度。由于对最优功率分配方法复杂度的理论分析较为困难，这里采用平均处理时间作为复杂度评估指标。将 4种功率分配方法在 3GHz Pentium IV 1GB-RAM个人计算机的 MATLAB环境下执行，并采用MATLAB配置的tic/toc命令统计各种方法的处理时间。可以看出，与最优功率分配方法相比，所提出的功率分配方法有效地降低了计算复杂度。

图2 基站天线数M不同时4种功率分配方法的计算复杂度（处理时间）（服务用户数K=M，所提出方法的门限0.01=ϵ）

所提出功率分配方法的复杂度由迭代次数以及每次迭代中二分法的复杂度共同决定，而后者受到门限值ϵ的影响。图3对这两方面的复杂度进行了进一步分析。首先，从图3(a)中可以看出，所提出的方法相对于门限值ϵ具有很快的收敛速度，当ϵ≤ 0.01时，系统达到稳态性能。其次，图3(b)分析了基站天线数M对所提出方法的迭代次数的影响。可以看出，随着基站天线数的增长，所提出方法的迭代次数将缓慢增长。例如，当天线数由2增至16时，迭代次数仅由1.5增至3。这2方面因素共同使得所提出的功率分配方法具有较低的计算复杂度。

图3 所提出的功率分配方法的复杂度分析（服务用户数K=M）

6 结束语

本文研究了基于单天线功率约束和ZF预编码的低复杂度功率分配方法。证明了最优功率分配具有多水平面的灌水结构，并由此提出了一种新的功率分配方法。仿真结果表明，与最优功率分配方法相比，所提出的功率分配方法能够以很小的性能损失为代价有效地降低计算复杂度，其性能优于现有的等功率分配和启发式方法。

附录 qsi(wi) 关于μ的单调性

设满足 qsi(wi)≥ 0 的μ的变量域为U，下面证明在变同的激活用户，即具有非零功率的用户。为了得到 qsi(wi)关于μ的显式表达式，将变量域U分为多个区域 Uj，的激活用户组合，记为πj。

对于 μ ∈Uj，由式(16)可知功率分配 p (wi) 为

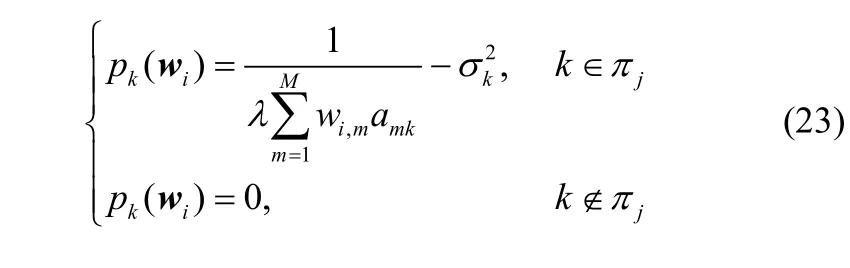
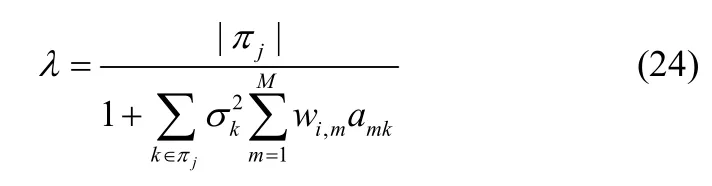
由式(23)和式(24)可得：

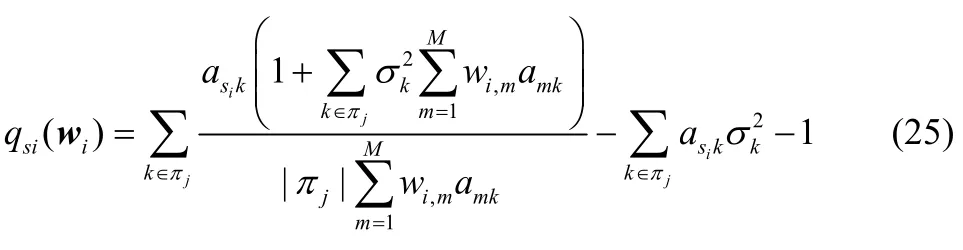
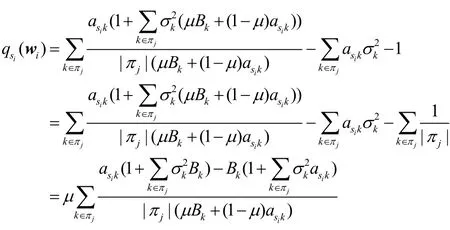
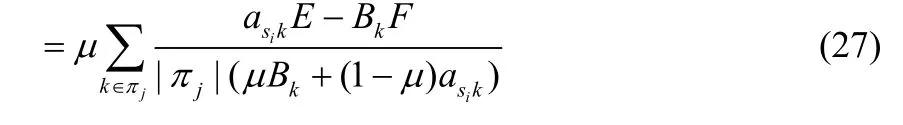
下面证明 qsi(wi) 关于μ的一阶导 ∇ qsi(wi) 是非负的。由式(27)可得

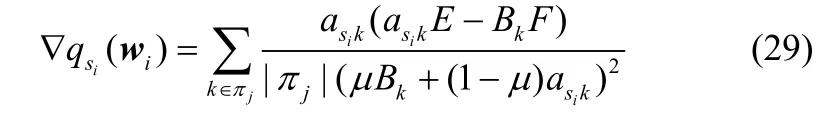
类似地，当 asikE - BkF≤ 0 时，可以证明式(30)给出的不等式仍然成立。因此， ∇ qsi(wi) 的下限可以表示为

由于E＞0、F＞0以及0≤μ≤1，因此μE/F+(1-μ)＞0。同时，根据式(28)和式(31)，可知∇qsi(wi) ≥ 0 。

按照以上的方法，可以证明 qsi(wi) 在每个区域 Uj上都是μ的单调递增函数， j = 0 ,…, J 。尽管 qsi(wi) 在 Uj的边界点可能不可求导，但是考虑到 wi是U上的连续函数，这使得λ和 p (wi) 也都是U上的连续函数，因此在变量域U上 qsi(wi) 是μ的单调递增函数。

[1] GESBERT D, KOUNTOURIS M, HEATH JR R, et al. Shifting the MIMO paradigm: from single user to multiuser communications[J].IEEE Signal Processing Mag, 2007, 24(5):36-46.

[2] DIMIC G, SIDIROPOULOS N D. On downlink beamforming with greedy user selection: performance analysis and a simple new algorithm[J]. IEEE Trans Signal Processing, 2005, 53(10): 3857-3868.

[3] WIESEL A, ELDAR Y C, SHAMAI S. Zero-forcing precoding and generalized inverses[J]. IEEE Trans Signal Processing, 2008, 56(9):4409-4418.

[4] GESBERT D, HANLY S, HUANG H, et al. Multi-cell MIMO cooperative networks: a new look at interference[J]. IEEE J Select Areas Commun, 2010, 28(9) :1380-1408.

[5] ZHANG R. Cooperative multi-cell block diagonalization with perbase-station power constraints[J]. IEEE J Select Areas Communication,2010, 28(9):1435-1445.

[6] YOO T, GOLDSMITH A. On the optimality of multiantenna broadcast scheduling using zero-forcing beamforming[J]. IEEE J Select Areas Commun, 2006, 24(3): 528-541.

[7] BOCCARDI F, HUANG H. Zero-forcing precoding for the MIMO broadcast channel under per-antenna power constraints[A]. Proceedings of IEEE Signal Processing Advances in Wireless Communications (SPAWC)[C]. Cannes, France, 2006. 1-5.

[8] VU M. MISO capacity with per-antenna power constraint[J]. IEEE Trans Communication, 2011, 59(5):1268-1274.

[9] BOYD S, VANDENBERGHE L. Convex Optimization[M]. Cambridge, UK: Cambridge University Press, 2004.

[10] TOLLI A, CODREANU M, JUNTTI M. Cooperative MIMO-OFDM cellular system with soft handover between distributed base station antennas[J]. IEEE Transactions Wireless Communication, 2008, 7(4):1428-1440.

[11] KARAKAYALI K, FOSCHINI G, VALENZUELA R. Network coordination for spectrally efficient communications in cellular systems[J].IEEE Wireless Communication Magazine, 2006(4), 13: 56-61.

[12] PALOMAR D P, FONOLLOSA J R. Practical algorithms for a family of waterfilling solutions[J]. IEEE Transactions Signal Processing,2005, 53(2): 686-695.