基于球形固结模型的桩端后注浆残余应力理论研究

张忠苗，何景愈,，房 凯

（1.浙江大学 岩土工程研究所，杭州 310058；2.浙江大学 软弱土与环境土工教育部重点实验室，杭州 310058；3.广西壮族自治区南宁市城乡建设委员会，南宁 530029）

1 引 言

桩端后注浆是指钻孔灌注桩在成桩后，采用高压注浆泵将一定压力的水泥浆经预埋的注浆通道压入桩端土层，通过增强桩端土和桩侧土的强度来提高桩基极限承载力、减少群桩沉降量的一项技术措施[1－2]。研究表明，桩端后注浆会产生残余应力，并对后注浆桩承载性状产生影响[3]。迄今为止，国内外对桩端后注浆残余应力的研究很少，仅知道残余应力会对后注浆桩极限承载力、侧摩阻力和端阻力造成一定的影响，严重时会引起桩体或管线的上抬[3－8]。

灌注桩在注浆过程中高压浆液对桩端土体产生很大的压力，在周围土体中产生超孔隙水压力，注浆结束后注浆压力不能及时消散，会在桩端产生残余应力，在压力的作用下引起桩端土的固结，孔隙水压力逐渐消散，土体有效应力逐渐增长。同时，桩端土中孔压的消散过程也是桩端残余应力消散的过程。

本文在球形空腔扩张及一维径向固结理论的基础上，对桩端后注浆桩的桩端注浆残余应力进行理论研究，在负指数衰减的初始超静孔隙水压力分布基础上，得到了残余应力随时间及扩散半径消散的解析解，同时对模型的主要影响参数进行了分析。实测数据表明，该解析解能有效地模拟后注浆残余应力的消散，研究结果对后注浆残余应力的理论研究及工程实践有重要的指导意义。

2 数学模型的建立

2.1 初始时刻注浆残余应力的分布

桩端后注浆浆液的扩散机制及注浆压力的分布是十分复杂的，是目前仍待研究的课题[1]。要精确地考虑注浆压力随时间及扩散半径的变化将使问题变得极其复杂，并难以求解。本文按照下述初始超静孔隙水压力的分布规律来简化模拟注浆结束时浆液扩散半径范围内注浆残余应力的分布。

Vesic[9]提出球形空腔扩张引起的初始超静孔隙水压力可用下式来估算：

式中：su为土体不排水强度；u(l,0)为由球形空腔扩张引起的超静孔隙水压力；l为相应点到孔中心的距离；l0为空腔扩张半径，即注浆管半径，一般为0.03～0.05 m；lp为塑性区半径；αf为破坏时的Henkel孔隙水压力参数；αe为Henkel孔压弹性系数。

式（1）虽然考虑了土体中塑性区的影响，但利用时需要测定较多的土工参数，故式（1）不便于实际的工程应用。朱小林等[10]也曾指出，超孔隙水压力的初始分布并不完全符合式（1）所示的对数型衰减规律，而更可能符合负指数型衰减：

式中：α为正值，一般取0.15～0.40之间，α宜取高值[10]，且α取0.3～0.4对初始孔压分布影响不大；ρ为径向距离比，ρ=l/l0；u0为空腔l0处初始超静孔隙水压力，此处为注浆结束时注浆管端处的残余应力值。

2.2 残余应力消散的固结微分方程

注浆结束后，注入桩端浆液因渗透和压滤作用而逐渐消散。注浆残余应力，即超孔隙水压力以注浆管端为中心向四周消散，周围的土体经历着一个固结过程。假设土为理想均匀各向同性饱和土体，这一课题属球空腔固结课题。为了能得到该问题的解答，作如下的假设和简化：

（1）土体为理想均匀各向同性弹性饱和土体；

（2）土颗粒和孔隙水在固结过程中体积是不可压缩的，土体固结变形为小变形；

（3）只考虑径向渗流和位移，忽略竖向渗流和位移的影响，土中孔隙水的渗流服从达西定律；

（4）固结过程中，整个研究区域的固结系数及渗透系数相同且保持不变；

（5）注浆浆液为幂律流体，浆液在扩散及衰减过程中处于层流运动；

（6）注浆持续时间t′内，注浆压力以球形方式向四周均匀扩散，初始残余应力分布服从负指数型衰减。

在上述假设的基础上，任意排水条件下的土体中球空腔固结微分方程可以表示为如下数学形式：

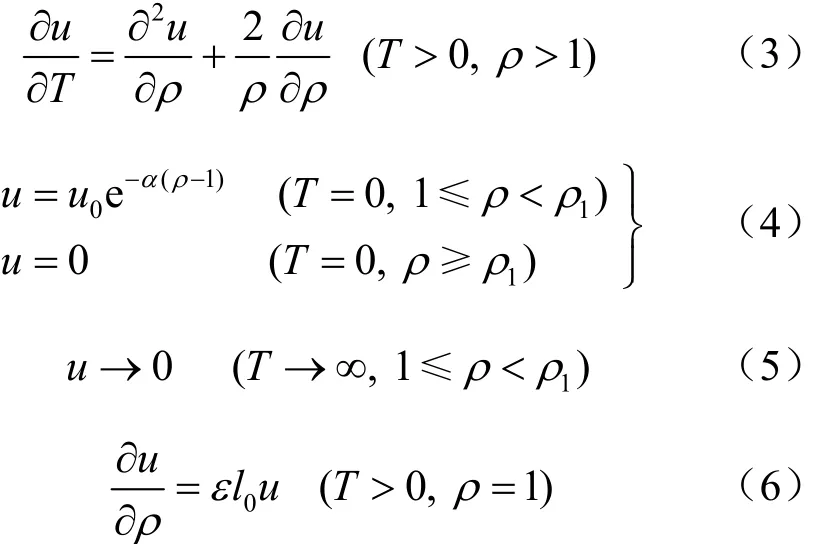
式中：T为时间因素，且 T=ct/(l1-l0)2，对桩端后注浆来说，浆液在桩端有一个扩散半径l1，认为是注浆的影响半径，在该范围以外认为孔隙水压力等于该地层的初始水压力，不产生超孔压，故时间因素T的计算公式中的排水路径取为l1-l0；c为土体固结系数，c=Esk/γw，Es为土体的压缩模量，k为土体的渗透系数，γw为水的重度；t为固结时间，即残余应力的消散时间；ε为孔壁处边界透水系数（ε=0，为不透水；0＜ε＜∞，为半透水；ε=∞为透水）。ρ1=l1/l0，l1为注浆浆液经过注浆持续时间t′后浆液最终扩散半径，按照不同的流型及浆液流体可推出不同的浆液扩散半径公式，根据以往的工程经验，注浆浆液水灰比一般取 0.5～0.8[11]，该水灰比范围水泥浆可认为是幂律流体[12]，l1可按下式确定，具体推导过程可参见杨秀竹等[13]的研究：

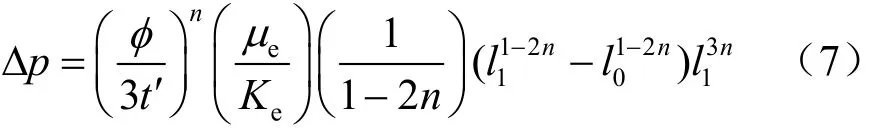
图1 浆液球形扩散理论模型Fig.1 Spherically spreading model of grout

2.3 模型的求解

微分方程组式（3）～（6）一般可用分离变量法进行求解。

令V(ρ,T)=Γ(T)⋅R(ρ)=ρu(ρ,T)，Γ(T)、R(ρ)分别为T与ρ的单值函数，经过一系列地推导，可得到方程的解答如下，推导过程可参见朱小林等[10]的研究：

式中：λ为任意正实常数；A(λ)=(1+εl0) C(λ)、B(λ)=λC(λ)、C(λ)为λ的任意函数，由初始条件确定。

式（8）的全部解为按λ在区间(0,∞)内的积分叠加，即

式中：M为任意常数，令M=1/π，结合初始条件V (ρ,0)=f (ρ)，则有

简化后，式（9）可转换为

上式在转换过程中，为避免混淆，已将余弦和正弦变换中的变量ρ换成为 x，花括号内的积分式可由下式确定：

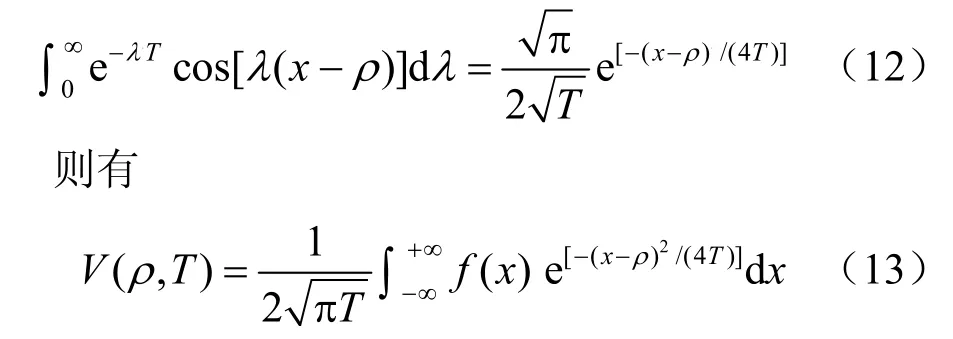
代入初始条件式（4），因式（4）是定义在[1,+∞)的范围内的，为求解式（13）在(-∞,+∞)范围内的积分，可按照解析开拓原理将式（4）所确定的函数解析开拓到整个(-∞,+∞)区域内，即

3 简化算法

若不考虑浆液扩散半径的影响，则式（14）为

朱小林等[10]给出了式（13）的另一个解答，为

按式（18）可绘出注浆残余应力随距离和时间变化的规律，如图2所示。

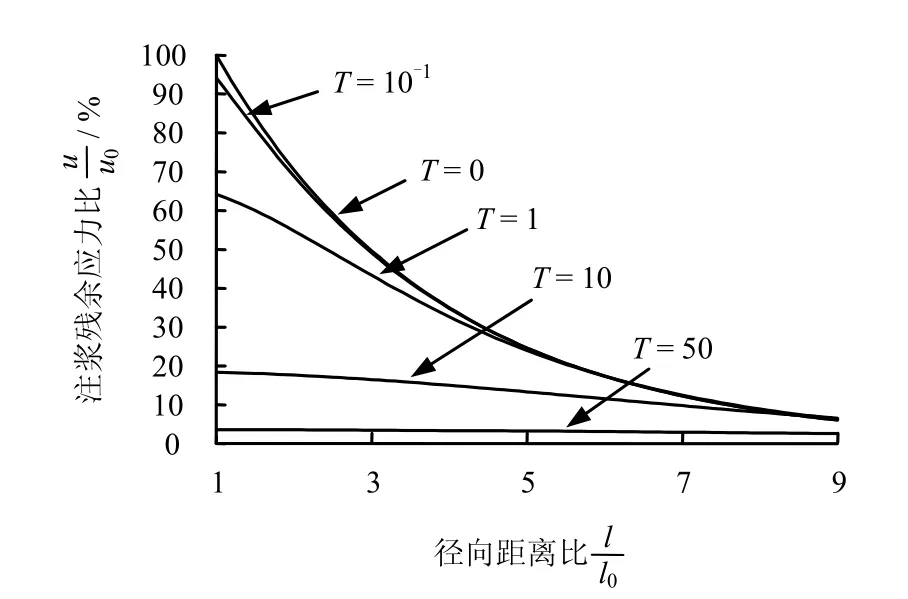
图2 注浆残余应力随时间与径向距离比的变化Fig.2 Variation curves of residual stress with time and radial distance ratio

从图中可以看出，代表不同固结阶段（T分别等于0、1 0-1、1、10、50）的各条曲线，在ρ=9处基本上已汇交。可以认为，ρ＞9及更远处注浆残余应力在整个固结过程中基本上没有变化，随着固结的持续，最终趋向于0。

4 参数分析

根据以上模型推导过程，影响注浆残余应力的主要因素有流变指数 n、幂律流体的稠度系数 C、土体的渗透系数k、土体的压缩模量Es、注浆持续时间t′及固结时间t。这6个参数都有明确的物理意义，可在实际试验中测得，对6个主要因素进行分析，并对比本文及简化算法，结果如图3～8所示。

从图3可以看出，流变指数n对注浆残余应力影响较大，两种方法的计算结果都随流变指数n的增大而迅速减小；径向距离比为1处，随着流变指数n从0.15增加到0.40，本文算法计算注浆残余应力比的结果从 89.68%减小到 65.21%，而简化算法结果则从 81.55%减小到 21.63%，可见简化算法结果随流变指数增大的减少幅度更大。

从图4可以看出，稠度系数C对注浆残余应力也有较大的影响，两种方法的计算结果都随C的增大而减小；径向距离比为1处，随着C从0.15增加到 0.40，本文算法计算结果从 89.68%减小到71.00%，而简化算法结果则从 55.10%减小到24.74%。

从图 5中可以看出，随着渗透系数 k从1.1×10-5m/s减小到 1.1×10-7m/s，两种算法计算注浆残余应力比的结果变化不大，但随着 k从1.1×10-7m/s减小到1.1×10-9m/s，简化算法计算的结果变化还是很小，而本文算法计算结果则发生了较大的变化，如径向距离比为1处，本文算法计算结果从89.68%减小到43.23%。

图3 流变指数n对注浆残余应力的影响Fig.3 Influence of rheological index on residual stress

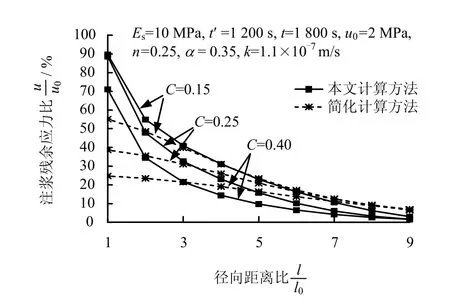
图4 稠度系数C对注浆残余应力的影响Fig.4 Influence of consistency index on residual stress

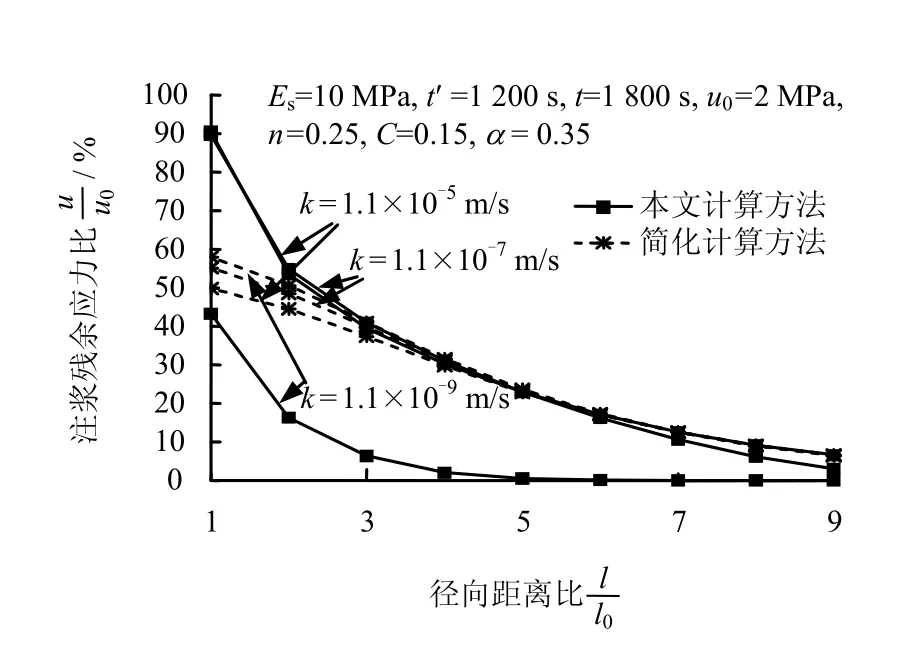
图5 渗透系数k对注浆残余应力的影响Fig.5 Influence of permeability coefficient on residual stress

由图6可以看出，压缩模量Es对注浆残余应力也有较大的影响，两种方法的计算结果都随Es的增大而减少；径向距离比为 1处，随着Es从 1 MPa增加到100 MPa，本文算法计算结果从90.17%减小到 74.85%，而简化算法结果则从 91.20%减小到12.60%。分析原因主要是土体压缩模量的增加会造成注浆残余应力消散的加快。同时还可以发现，压缩模量对简化算法的计算结果影响更大，而当Es=1 MPa时两种方法计算结果较为接近。

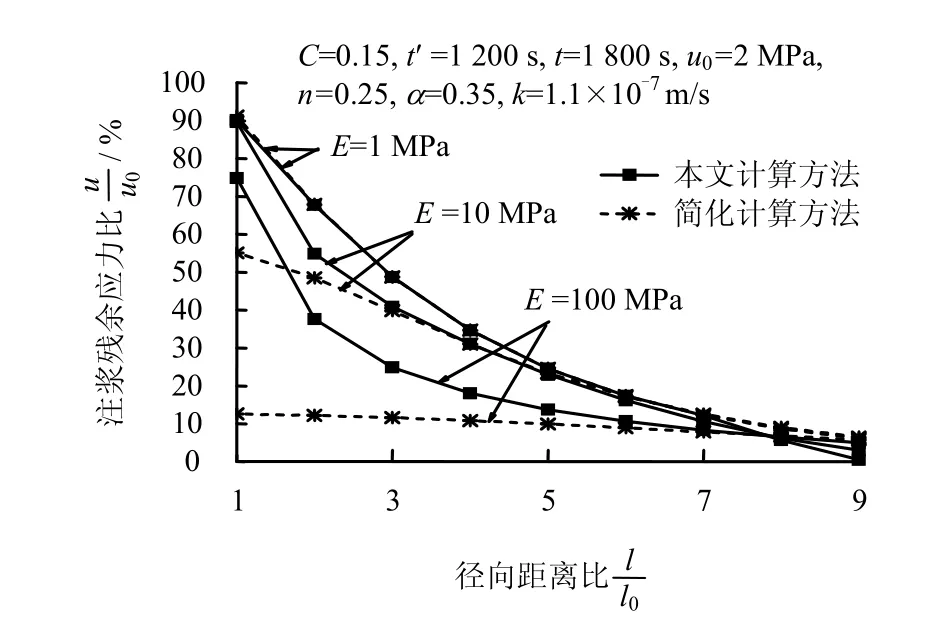
图6 压缩模量Es对注浆残余应力的影响Fig.6 Influence of compression modulus on residual stress

由图 7可以看出，随着注浆持续时间t′从1200 s增加到3600 s，两种方法计算的注浆残余应力结果都有所增大，但变化并不明显，工程中注浆持续时间一般在20 min（1200 s）左右。

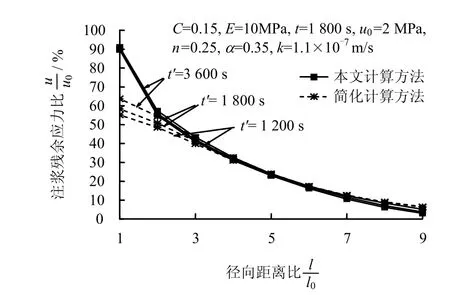
图7 注浆持续时间 t′对注浆残余应力的影响Fig.7 Influence of injection time on residual stress

由图8可以看出，随着固结时间t的增加，两种算法计算的注浆残余应力结果都迅速减少；径向距离为1处，24 h（86400 s）后，简化方法计算注浆残余应力结果只有2.22%。

5 模型验证

图8 固结时间t对注浆残余应力的影响Fig.8 Influence of consolidation time on residual stress

试验场地为杭州市奥体博览中心项目，该工程的场地土性质较差，分布着较厚的粉土与黏性土。试验采用桩径为800 mm的钻孔灌注桩，桩长为39.2 m，成桩15 d后，将3.5 t水灰比为0.6的水泥浆通过注浆管注入桩端。注浆时，注浆泵输出压力约为1.0～1.5 MPa；注浆结束后，桩端附加压力逐渐消散：注浆刚结束时，桩端附加压力为 0.678 MPa；经过30 min，桩端附加压力为0.251 MPa；经过90 min，桩端附加压力为0.169 MPa；经过24 h，桩端附加压力为0.067 MPa。

对比简化方法与本文方法，计算注浆残余应力结果如表1所示，其中主要参数取值如下：注浆持续时间t′取 1200 s，α=0.35，土体Es=35 MPa，k=1.1×10-5m/s，稠度系数C=0.15，n=0.25，详细的试验情况及注浆参数见邹健等[3]的研究。

表1 注浆残余应力计算与实测结果比较Table1 Comparison of residual stresses between calculation and measurement

从表1中可以看出，通过简化方法计算所得注浆残余应力扩散过快，结果偏小，基本上没有反映出真实的消散情况，30 min时5%的结果基本上可以忽略。而本文的方法虽然得到的结果偏大，但总体上能够对残余应力消散的变化趋势作出较好的模拟，且偏于保守，鉴于后注浆过程中存在着很大的不确定性，该精度的结果可达到预测的要求。

6 结 论

（1）基于球形空腔扩张及一维径向固结理论，对注浆桩的桩端注浆残余应力进行理论研究，在负指数衰减的初始超孔隙压力分布基础上，得到了残余应力随时间及扩散半径消散的解析解。

（2）在不考虑注浆扩散半径的前提下，对该解析解进行了简化，与本文的计算方法相比较，对模型主要影响因素参数分析发现，流变指数、稠度系数、土体的压缩模量及固结时间是影响注浆残余应力的关键因素，注浆残余应力一般会随着流变指数、稠度系数、土体的压缩模量或固结时间的增大而减小。

（3）用本文方法计算注浆残余应力的结果总体上能够对残余应力消散的变化趋势作出较好的模拟，证明了该计算模型的可靠性。

[1]张忠苗. 灌注桩后注浆技术及工程应用[M]. 北京: 中国建筑工业出版社,2009.

[2]张忠苗,张乾青. 后注浆抗压桩受力性状的试验研究[J].岩石力学与工程学报,2009,28(3): 475－482.ZHANG Zhong-miao,ZHANG Qian-qing. Experimental study on mechanical properties of post-grouting compressive pile[J]. Chinese Journal of Rock Mechanics and Engineering,2009,28(3): 475－482.

[3]邹健,张忠苗,林存刚. 桩端后注浆桩残余应力研究[J].岩石力学与工程学报,2011,30(增刊1): 3275－3280.ZOU Jian,ZHANG Zhong-miao,LIN Cun-gang.Analysis of residual stress on post grouted drilled shaft[J].Chinese Journal of Geotechnical Engineering,2011,30(Supp.1): 3275－3280.

[4]刘利民,李增选. 残余应力及其对桩承载性状的影响[J].特种结构,2000,17(4): 16－18.LIU Li-min,LI Zeng-xuan. Residual pile stress and its influence to pile bearing capacity[J]. Special structures,2000,17(4): 16－18.

[5]印长俊,王星华,马石城. 灌注桩残余应变的产生机制分析[J]. 工程力学,2009,26(7): 125－133.YIN Chang-jun,WANG Xing-hua,MA Shi-cheng.Analysis of generating mechanism of residual strain in cast-in-place piles[J]. Engineering Mechanics,2009,26(7): 125－133.

[6]张忠苗,张广兴,吴庆勇,等. 钻孔桩泥皮土与桩间土性状试验研究[J]. 岩土工程学报,2006,28(6): 695－699.ZHANG Zhong-miao,ZHANG Guang-xing,WU Qing-yong,et al. Studies of characteristics of mudcake and soil between bored piles[J]. Chinese Journal of Geotechnical Engineering,2006,28(6): 695－699.

[7]袁敬强,陈卫忠,谭贤君,等. 软弱地层注浆的细观力学模拟研究[J]. 岩土力学,2011,32(增刊2): 653－659.YUAN Jing-qiang,CHEN Wei-zhong,TAN Xian-jun,et al.Mesomechanical simulation of grouting in weak strata[J].Rock and Soil Mechanics,2011,32(Supp.2): 653－659.

[8]刘俊伟,俞峰,张忠苗,等. 基于能量守恒的预制桩施工残余应力模拟[J]. 岩土力学,2012,33(4): 1227－1232.LIU Jun-wei,YU Feng,ZHANG Zhong-miao,et al.Simulation of post-installation residual stress in preformed piles based on energy conservation[J]. Rock and Soil Mechanics,2012,33(4): 1227－1232.

[9]VESIC A S. Expansion of cavities in infinite soil mass[J].Soil Mechanics and Foundations Division，Proceedings of ASCE,1972,98(SM3): 265－290.

[10]朱小林,唐世栋. 利用孔隙水压力-静力触探探头估算软黏土固结系数的理论分析[J]. 工程勘察,1986,(6): 8－12.ZHU Xiao-lin,TANG Shi-dong. Theoretic analysis of the estimation of consolidation coefficient by piezocone tests[J]. Geotechnical Investigation and Surveying,1986,(6): 8－12.

[11]张雁,刘金波. 桩基手册[M]. 北京: 中国建筑工业出版社,2009.

[12]阮文军. 基于浆液黏度时变性的岩体裂隙注浆扩散模型[J]. 岩石力学与工程学报,2005,24(15): 2709－2714.RUAN Wen-jun. Spreading model of grouting in rock mass fissures based on time-dependent behavior of viscosity of cement-based grouts[J]. Chinese Journal of Rock Mechanics and Engineering,2005,24(15): 2709－2714.

[13]杨秀竹,雷金山,夏力农,等. 幂律型浆液扩散半径研究[J]. 岩土力学,2005,24(增刊2): 5862－5867.YANG Xiu-zhu,LEI Jin-shan,XIA Li-nong,et al. Study of grouting diffusion radius of exponential fluids[J]. Rock and Soil Mechanics,2005,24(Supp.2): 5862－5867.