隧道纵向整体抗震分析的近似方法

张斌伟，严松宏，杨永东

（1.陇东学院 岩土与建材研究所，甘肃 庆阳 745000；2.兰州交通大学 土木工程学院，兰州 730070）

1 引 言

随着地下工程的不断发展和利用，地下结构的抗震设计问题已经成为一个十分重要的课题，越来越受人们的重视。国内外学者对地下工程的抗震问题开展了大量的研究，文献[1－6]对地下结构抗震分析的拟静力方法进行了详细地论述，地下工程的抗震分析可分为横截面抗震分析和纵向整体抗震分析。横向抗震设计方法可求得地下结构横断面内的应力与变形，然而，由于地下结构是一种埋设在地层介质中的空间延伸结构，在地震作用下的纵向变形和内力以及沿其长度地震响应也是不容忽视的。在地下结构的抗震分析中，比较常用的一种经典方法是反应位移法，该法将地下结构视为放置于弹性地基上的梁，首先计算得到在地震作用下的地基变形，地基变形模式如图1所示。然后将该变形直接作用于结构上，按弹性地基梁理论求得结构的内力，从而进行结构抗震验算。它是以研究地基变形为重点，没有考虑结构与围岩的相互作用，求得的结果是偏于保守的。而且，也没有从理论上说明隧道结构的地震惯性力对其抗震的影响。这对于深埋结构是可以，但对于大型的浅埋结构是不太安全的。鉴于地下工程的复杂性，从宏观上研究隧道埋深、地层剪切波速、基岩剪切波输入方向、上覆地层的特征周期、弹性地基系数及围岩弹性模量对隧道衬砌纵向应力的影响，对于隧道结构抗震的概念设计具有重要意义，而且研究围岩-结构相互作用以及隧道地震惯性力对其抗震分析的影响，对于理清目前隧道抗震界的一些认识具有重要的意义。

图1 地层变形模式Fig.1 Deformation mode of strata

2 地下结构的当量半径简介

许多研究资料表明，地下结构的形状对周围应力分布有影响，但限于目前弹塑性力学及岩石力学的发展水平，除圆形、椭圆形等少数断面形状周围的应力分布有理论解析解外，半圆拱形、矩形等许多地下工程常用的断面形状周围的应力分布都缺乏精确的理论解析解。这些形状的地下结构所引起的应力重分布，多通过光弹性试验及计算机数值模拟方法来研究确定。虽然通过计算机数值模拟等方法可以准确地获得地下结构周边的应力分布情况，但在工程中想应用这些计算结果却往往比较困难。而且，重点凸显这些形状特点形状效应多局限在棱角等局部地方，对总体地层空间应力场的演变变化规律影响不大。因此，对非圆形的断面形状其他形状地下结构，采用当量半径的折算形式，将其折算成标准圆形隧道来分析和计算，不但有利于问题的理论分析，而且易于工程现场实际应用。具体的确定方法可参考李世辉[7]的成果。

3 隧道纵向抗震分析模型

将隧道视为置于弹性地基上的结构，传统的分析方法以地基为研究对象，将地基的变形作用于梁上，来反求结构的内力，没有考虑结构-围岩的相互作用。这里，仍将隧道视为置于弹性地基上的梁，只不过以隧道结构本身为研究对象，建立结构振动微分方程来求解隧道内力及变形。隧道-围岩体系的地震变形如图2所示。

为了便于计算，模型做出如下假设：

（1）土层为水平分层的半无限各向同性均匀线性弹性介质；

（2）视隧道为弹性地基梁，即隧道与围岩之间为弹簧连接；

（3）隧道与围岩之间存在相互作用，考虑隧道与围岩之间的相对位移。隧道在地震作用下产生变形，其变形包括轴向变形和横向变形。下面分别建立隧道轴向和横向的运动方程。

图2 隧道-围岩体系的变形图Fig.2 Deformation diagram of tunnel and surrounding rock system

4 隧道纵向整体抗震分析

4.1 隧道运动方程的建立

从地震作用产生地层和结构变形的角度来看，隧道作为埋设于地下的线状结构，与地下管线的变形具有很大的相似性，故利用文献[8]研究的基本思想建立隧道运动方程。从地基梁上取出长度为dx的单元作为自由体进行分析，如图 3所示。已知：E为梁的弹性模量，I为梁截面惯性矩，A为梁截面面积，Kw为地基梁横向变形系数，Ka为地基梁轴向变形系数，v(x,t)为隧道的横向位移，u(x,t)为隧道的轴向位移；gw(x,t)为地基土的横向位移，ga(x,t)为地基土的轴向位移。建立梁单元横向动平衡方程得：

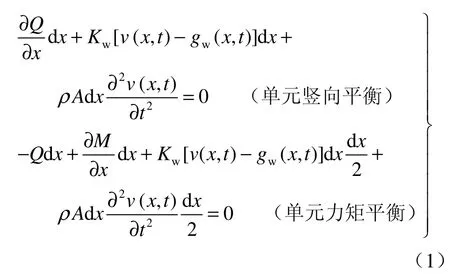
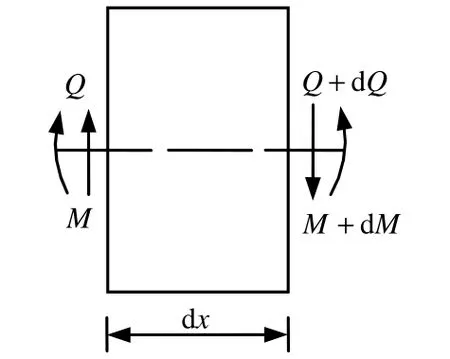
图3 隧道单元受力图Fig.3 Force diagram of tunnel unit

根据材料力学及隧道弯曲刚度EI不随 x变化的假定，最后得地震波作用下隧道二维运动方程为

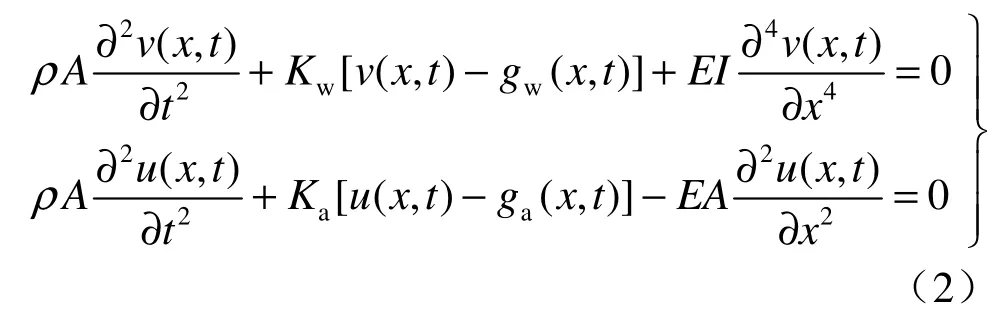
如果不考虑隧道的地震惯性力，则上述动平衡方程可写成如下公式：

考虑到隧道沿纵向存在施工缝，对刚度EI采用折减，可取理论刚度的 2/3。对于式（2）、（3）的处理目前有两种思路：

（1）直接解这两个常微分方程，为了数学上的方便，通常还进行了一定的简化[9]。

（2）利用隧道与围岩的相互作用原理，许多实践证明，考虑到在地震波作用下地基振动的波形与隧道振动的波形很相似的特点，引入了变形传递系数的概念，使上述方程的求解成为可能。

4.2 变形传递系数的求解

为了便于从宏观上研究隧道埋深、地层剪切波速、基岩剪切波输入方向、上覆地层特征周期、弹性地基系数及围岩弹性模量对衬砌纵向应力的影响，对于地震波作如下假定：不考虑地震波的随机性、时频特性及在土层中的反射和散射，将地震波看成是单一频率的简谐波。这种假设与实际的随机地震波相差较大，但由于对结构产生显著影响的是几个主要频率的波，其他频率影响不大。而且从本文研究的内容和目的来看也是可行的。如果要定量研究地震波产生的内力，就必须考虑地震波的随机性、时频特性等。基于以上假定，地震波动形状函数可写为

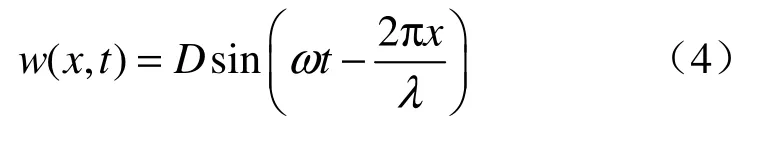
式中：ω为地震波的圆频率（Hz）；λ为地震波长（m）；D 为地基土的变位振幅（m）；假定地震波为S波，入射方向与隧道的轴线成φ角，剪切波的位移使地基土产生横向位移和轴向位移分别为

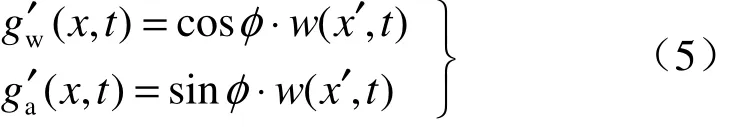
利用隧道与围岩的相互作用原理，引入了横向变形传递系数wξ和轴向变形传递系数aξ，则隧道横向和轴向振动时的位移可表示为

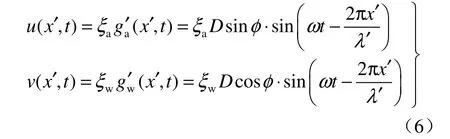
将式（6）代入式（2），并利用式（5），可得考虑隧道地震惯性力的位移传递系数ξw和ξa为

当不考虑隧道结构自重时，可直接取β=0即可。

4.3 隧道纵向地震应力的求取

利用前面推导的隧道位移u(x′,t)和v(x′,t)，可得隧道的轴向应变为

令λ=vsT ，vs为剪切波速（m/s），T为场地的固有振动周期（s）；假定基岩固定，基岩上覆层的厚度为 H，距离地表面任意深度z处的土层振动振幅D(z)可近似表示为[10]

式中：Sv为土层的速度反应谱。则隧道平面处的地层振幅可近似表示为

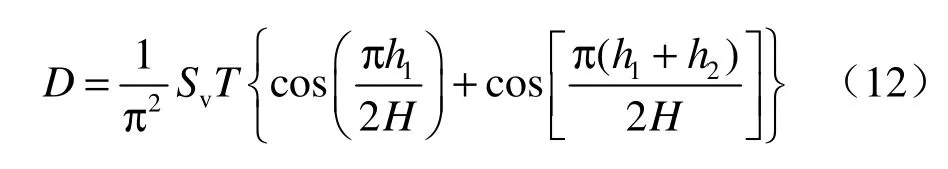
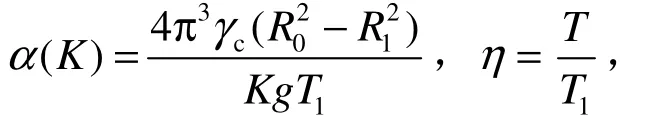
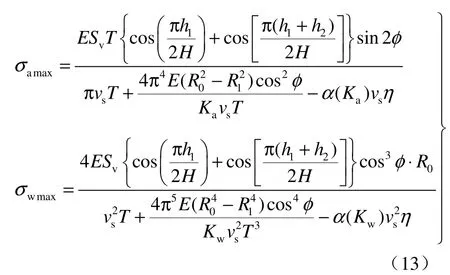
以上是基于围岩-隧道结构相互作用，考虑隧道地震惯性力影响。当不考虑隧道自重惯性力时，可直接取 α(K)=0即可。若不计围岩-结构的相互作用，可取ξw=1，ξa=1，则最后可得隧道应力的计算公式为

最后考虑到地震作用的随机性和作用方向的不确定性，则此时隧道结构的纵向应力组合为

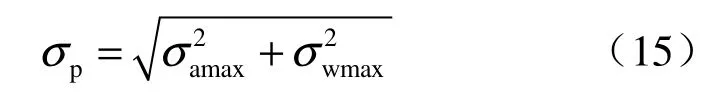
5 各项计算参数的确定

5.1 地层的简化[11]

地震时地层的实际变形十分复杂，为简化计算可以将多层地层换算为单一地层。换算后单一地层的力学物理参数如下：单位体积重度 γ=∑γihi/H，动泊松比 μd=0.45，剪切波速 vs=H/∑ (hi/vsi)，动剪切模量 Gd=，动弹性模量 Ed=2(1-μd)⋅Gd。

5.2 场地固有周期T[11]

场地固有周期一般根据建设地点的剪切波速计算。由多层土构成的场地固有周期特征值TG=4 ∑ hi/vsi，但由于地震发生时的地层应变大于勘测时的地层应变，考虑应变水平，取 T=1.25TG，也可以通过场地平面有限元分析求固有周期T。

5.3 弹性剪切波速vs的确定[12]

剪切波的行进速度，应由勘察报告提供，但应考虑到实测条件与强震时不同，应按勘察报告提供实测数值的2/3采用。

5.4 震动基准面的速度反应谱Sv

震动基准面的速度反应谱满足

式中：KH为设计水平地震系数（未考虑埋深和场地修正）；Sv1为单位地震系数的速度反应谱（m/s），根据场地固有周期，由图4可查得。

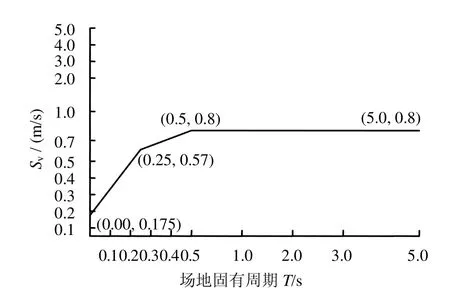
图4 单位水平地震系数的速度反应谱[11]Fig.4 Velocity response spectrum of unit horizontal seismic coefficient[11]

5.5 弹性地基系数Ka和Kw[12]

弹性阻抗系数亦可称为“地基反力系数”。此项系数的确定比较复杂，不仅与结构外缘的做法、场地土质相关，还与隧道结构的施工方法密切相关。关于Ka和Kw值的确定，日本《化工设备抗震准则》[6]提供了更为简化的方法，认为

式中：Gs为地基土的剪切模量。

6 算例分析

某山岭隧道，地层比较单一，其地层参数见表1，围岩参数见表2，隧道支护参数见表3。考虑以下参数发生变化时的隧道纵向应力的变化，研究影响隧道纵向抗震的因素。

表1 地层参数Table1 Parameters of stratum

表2 围岩参数Table2 Parameters of rock mass

表3 隧道参数Table3 Parameters of tunnel

(a) 结构-围岩相互作用对衬砌纵向应力的影响；(b)考虑隧道埋深及自重惯性力对衬砌纵向应力的影响；(c)上覆地层的特征周期对衬砌纵向应力影响；(d) 弹性地基刚度系数为 Ka=Kw=βG，β改变时对衬砌纵向应力的影响；(e) 围岩弹性模量变化时对衬砌应力的影响。

6.1 结构-围岩相互作用对衬砌纵向应力的影响

围岩-结构相互作用对衬砌纵向应力的影响，如图5所示。由图可知，当隧道埋深一定时，总体上看，考虑相互作用得到的衬砌纵向应力要小于不考虑相互作用的情况；剪切波速越小，两者相差越大，随着剪切波速（围岩强度）的增大，两者差别越小，说明围岩强度越弱，相互作用对结构的影响越大，对于处于软弱围岩中的隧道工程十分重要。

另外可知，考虑围岩-结构相互作用，当剪切波速较小时，隧道以弯曲变形为主，当剪切波速较大时，隧道以轴向变形为主，并且随着剪切波速的增大，纵向应力减小。当不考虑相互作用时，弯曲应力总体上小于轴向应力，而且随着剪切波速的增大，衬砌纵向应力也是逐渐减小。

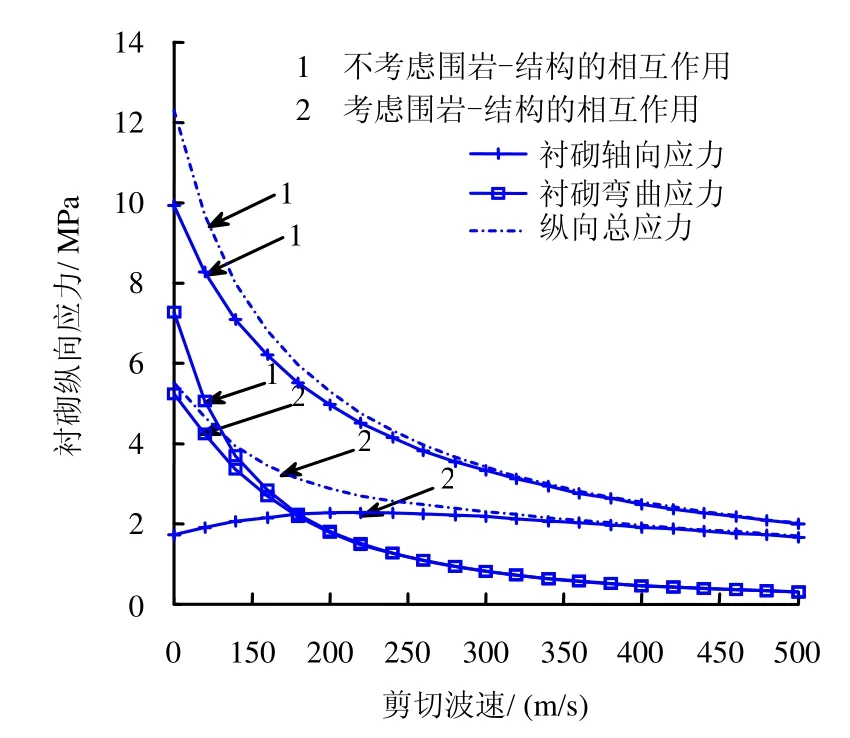
图5 围岩-结构相互作用对衬砌应力的影响Fig.5 Effects on lining stress due to interaction between rock and structure

6.2 隧道埋深和自重惯性力对衬砌纵向应力的影响

由于地层卓越周期与地层厚度及场地的硬度（平均剪切波速）密切相关，为了考虑隧道结构自重惯性力对其纵向抗震性能的影响，考虑以下两种情况。

（1）假定隧道地层埋深变化，进而卓越周期也变化，但场地的硬度不变（平均剪切波速不变），主要考虑的是隧道埋深对自重惯性力的影响，计算结果见表4。

表4 隧道自重惯性力对纵向应力的影响（考虑埋深的变化）Table4 The influence of inertial force of tunnel on longitudinal stress（considering the depth changes）

由表4可知，当隧道埋深较浅时，自重惯性力对隧道纵向总应力的影响比深埋隧道要大，也就是说，对于浅埋隧道自重惯性力的影响比较大。但从计算结果总体来看，自重惯性力是完全可以忽略的，这就是目前地下工程抗震计算不考虑结构自重惯性力的原因。这个结论的前提是围岩-结构完全满足变形协调的相互作用。但在山岭隧道的建设中，由于目前的新奥法施工方法，在洞顶势必要有一定的松散区，这部分岩体在地震作用下会产生较大的竖向松散岩体惯性力，这个惯性力对浅埋结构影响较大，这个结论在文献[13]中已经得到验证，因此，对于超浅埋隧道考虑结构的自重惯性力是必要的，但随着埋深的增大，结构自重惯性力的影响就可以完全忽略不计。

（2）假定隧道地层及地面均为水平，即隧道地层埋深不变，地层固有周期不变（实际上是变化的），研究场地软硬程度与结构自重惯性力的关系，计算结果见表 5。由表可知，随着隧道地层硬度的增大（剪切波速增大），隧道结构自重惯性力对纵向总应力的影响显著减小，也就是说，自重惯性力对软弱地层中的隧道的影响要大于在坚硬地层中的隧道结构。一般来讲，对同一个地层来说，地层的硬度与离地表的距离成正相关，从这点来看，得到与表 4一致的结论。

由图6可知，隧道弯曲和轴向应力随埋深的增大均减小，地层变形随距离地表深度的增大也逐渐变小，弯曲应力和轴向应力对入射角的变化很敏感，随着入射角的增大，结构由弯曲型逐渐变化为拉压型。同时，对于隧道等横截面较大的地下线状结构，其弯曲应力占有较大比重，不可忽视，这一点与地下管线不同，地下管线由于截面小，弯曲应力可以忽略而只考虑轴向拉压应力。

表5 隧道自重惯性力对纵向应力的影响(考虑剪切波速的变化)Table5 The influence of inertial force of tunnel on longitudinal stress (considering the variation of shear wave velocity)

图6 隧道埋深与衬砌纵向应力的关系Fig.6 Relationships between tunnel depth and longitudinal stress of lining

6.3 上覆地层特征周期及弹性地基刚度系数对隧道纵向应力的影响

由图7可知，地层水平和竖向变形随地层特征周期的增大而增大，衬砌弯曲应力随地层特征周期的增大而减小，轴向应力随地层特征周地期的增大而增大；对于地层特征周期和剪切波速小的场地，隧道以弯曲变形为主，相反，隧道以轴向变形为主；这一规律与隧道的埋深无关。衬砌纵向应力与弹性地基刚度系数有关，弯曲和轴向应力均随地基系数的增大而增大，轴向应力随地基系数的变化是敏感的，弯曲应力随地基系数的变化不敏感，当地基系数取为3时，纵向应力的增幅趋于平缓，故可以认为，在进行隧道的纵向地震分析时，取 Ka=Kw=3Gs，理论上是可行的。

6.4 围岩弹性模量对隧道纵向应力的影响

由图8可知，衬砌轴向和弯曲应力随围岩弹性模量的增大而增大，但当弹性模量增大到一定程度后，衬砌应力增长缓慢；弯曲和轴向应力的分界入射角随弹性模量的增大而减小，纵向总应力取最大值的入射角随围岩弹性模量的增大而减小，即当围岩的弹性模量较大时，较小的地震入射角就可能在衬砌中产生最大的纵向应力。同时，随入射角的增大，隧道从弯曲型变形逐渐改变为拉压型变形，当剪切波与基岩面法线夹角为 0°时，轴向应力最小，以弯曲变形为主；随着入射角的增大，轴向应力也逐渐增大，当入射角度为 90°时，此时剪切波沿着基岩面水平传播，对隧道的影响可以忽略不计。

图7 地层特征周期和弹性地基系数对衬砌纵向应力的影响Fig.7 Effects of characteristic period and elastic foundation coefficient on longitudinal stress of lining

图8 围岩弹性模量对衬砌纵向弯曲和轴向应力的影响Fig.8 Effects of rock mass elastic modulus on longitudinal stress and axial stress of lining

7 结 论

（1）笔者根据文献[8－10]的基本思想，以弹性地基梁为模型，考虑隧道结构-围岩相互作用，建立隧道动平衡微分方程，分析隧道埋深、地层剪切波速、基岩剪切波输入方向、上覆地层的特征周期、弹性地基系数及围岩弹性模量对衬砌纵向应力的影响，综合比较了这些因素对隧道应力和变形的影响。

（2）围岩-结构相互作用对隧道抗震分析具有重要的影响，考虑相互作用得到的衬砌应力要小于不考虑相互作用的结果，围岩强度越弱，相互作用对隧道的影响越大，这对处于软弱围岩中的隧道工程具有重要的意义。同时，从围岩-结构相互作用出发，结构自重惯性力对隧道抗震分析影响很小，尤其是随着埋深的增大，这种影响可以忽略不计，但由于目前山岭隧道施工技术的局限，隧道洞顶势必要形成松散区，而且超挖回填质量不能保证，使得相互作用效果不好，这部分岩体在地震作用下，会产生较大的竖向惯性力，因此，对于超浅埋隧道考虑惯性力是必要的。

（3）本文实质上是提出了隧道纵向应力的工程实用算法，适用于土层水平分层均匀的工程场地。该方法模型建立合理、推导过程严谨、理论上正确可行，对宏观上研究隧道在地震作用下的纵向反应具有积极的意义，对隧道整体抗震的概念分析具有一定的参考价值和指导意义。

[1]HASHASH Y M A,HOOK J,SCHMIDT B,et al.Seismic design and analysis of underground structure[J].Tunnelling and Underground Space Technology,2001,16(4): 247－293.

[2]INGERSLEV C,KIYOMIYA O. Earthquake analysis[J].Tunnelling and Underground Space Technology,1997,12(2): 157－162.

[3]韩大建,周阿兴,黄炎生. 珠江水下沉管隧道的抗震分析与设计(Ⅰ)——时程响应法[J]. 华南理工大学学报(自然科学版),1999,27(11): 115－121.HAN Da-jian,ZHOU A-xing,HUANG Yan-sheng.Seismic analysis and design of the Pearl River tunnel(Ⅰ)—Time domain response method[J]. Journal of South China University of Technology (Natural Science),1999,27(11): 115－121.

[4]韩大建,唐增洪. 珠江水下沉管隧道的抗震分析与设计(Ⅱ)——行波法[J]. 华南理工大学学报(自然科学版),1999,27(11): 122－129.HAN Da-jian,TANG Zeng-hong. Seismic analysis and design of the Pearl River tunnel(Ⅱ)—Traveling wavemethod[J]. Journal of South China University of Technology (Natural Science),1999,27(11): 122－129.

[5]阎盛海. 地下结构抗震[M]. 大连: 大连理工大学出版社,1989.

[6]JOHN S T,ZAHRAH T F. A seismic design of underground structures[J]. Tunnelling and Underground Space Technology,1987,2(2): 165－197.

[7]李世辉. 隧道支护设计新论(典型类比分析法应用与理论)[M]. 北京: 科学出版社,1999.

[8]黄强兵,彭建兵,杨天亮. 埋地管道在地震波作用下的抗震性能分析[J]. 工程勘测,2004,(3): 64－67.HUANG Qiang-bing,PENG Jian-bing,YANG Tian-liang.Analysis of anti-seismic properties of buried pipelines under the action of seismic waves[J]. Geotechnical Investigation and Surveying,2004,(3): 64－67.

[9]谷拴成,高宗褀. 土层隧道动力分析[J]. 西安科技大学学报,2002,22(4): 404－406.GU Shuan-cheng,GAO Zong-qi. Seismic analysis of tunnel in soil[J]. Journal of Xi'an University of Science and Technology,2002,22(4): 404－406.

[10]侯忠良. 地下管线抗震[M]. 北京: 学术书刊出版社,1990.

[11]黄先锋. 地下结构的抗震计算——位移法响应[J]. 铁道建筑,1999,(6): 3－6.

[12]沈世杰. 城市轻轨地下隧道结构抗震分析探讨[J]. 特种结构,2003,20(3): 1－3.SHEN Shi-jie. A discussion of structural seismic analysis of urban metro tunnel[J]. Special Structures,2003,20(3):1－3.

[13]杨小礼,李亮,刘宝琛. 强震作用下交通隧道的拟静态反应[J]. 中国公路学报,2001,14(4): 55－58.YANG Xiao-li,LI Liang,LIU Bao-chen. Response of transportation tunnels due to strong earthquake[J]. China Journal of Highway and Transport,2001,14(4): 55－58.