循环荷载作用下考虑颗粒破碎的堆石体本构模型

刘恩龙，陈生水，李国英，米占宽，韩华强

（1.四川大学 水利水电学院，成都 610065；2.南京水利科学研究院，南京 210029）

1 引 言

循环荷载作用时颗粒破碎对粗粒土的强度和变形特性有重要影响[1－3]。应力水平高时，颗粒不仅发生滑移、转动，还发生严重的颗粒破碎[4]，如何考虑循环荷载作用时颗粒破碎对堆石体的动应力-应变特性的影响是当前岩土工程急需解决的问题，以便为高土石坝的抗震设计提供理论依据[5]。

最近，已经建立了一些本构模型来考虑循环荷载作用时粗粒土的动应力、应变特性。所采用的方法主要是基于弹塑性理论[6－7]、边界面理论[8－13]和次塑性模型[14]等。与砂土相比，堆石体在较低的应力水平下就会发生严重的颗粒破碎，原因是砂土的粒径远小于堆石体的粒径，故砂土需要很高的应力作用才会发生颗粒破碎。对于200～300 m高的堆石坝，堆石体在受到正常运营情况下的应力水平作用时所产生的颗粒破碎会对其应力、应变特性产生重要影响。地震等循环荷载作用时处于高应力水平的堆石体的动力响应与砂土的也有很大不同[1]。建立的一些砂土的动本构模型，不能很好地模拟高坝中堆石体的动应力、应变特性，故有必要建立适用于堆石体的考虑颗粒破碎的动本构模型，以便于进行高土石坝的抗震分析。

基于堆石体颗粒破碎时临界状态性状的试验结果分析，笔者提出了颗粒破碎时临界状态线的数学表达式，并建立了堆石体的静载作用下的本构模型[15]。引入卸载、再加载模量和卸载模量，把已建立的静弹塑性本构模型推广到考虑循环荷载作用，并与堆石体的动三轴试验结果进行对比，以验证堆石体的动本构模型的正确性。

2 本构方程

2.1 临界状态

试验发现[15]，对于堆石体，不同的排水条件和固结应力作用下，试样最终都达到临界状态，且在q-p′平面（q为广义剪应力，p′为平均有效应力）和e-lgp′平面临界状态线均为非线性变化。堆石体的临界状态线在e-lnp′面上的表达式为

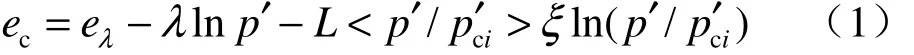
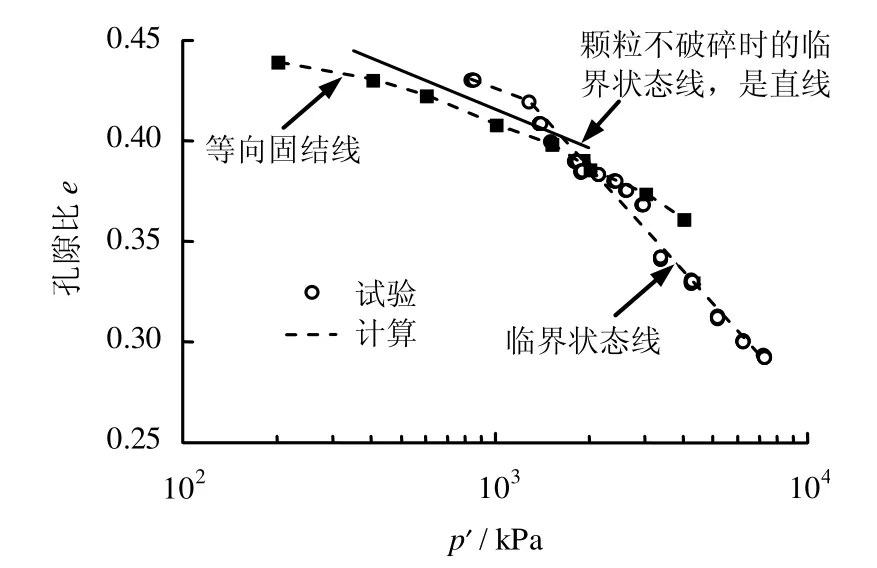
图1 实测堆石体的临界孔隙比[15]Fig.1 Tested critical void ratio of rockfill materials[15]

由此可见，随着应力水平的增加，堆石体逐渐发生颗粒破碎，达到临界状态时的临界状态线在e-lg p′平面中是一逐渐偏离初始颗粒不破碎时呈直线的临界状态线的曲线。对于堆石体来说，颗粒的破碎使得其临界状态时的粒径级配与初始级配相比发生了很大变化。由此，定义同样级配的试样是同一种材料，那么初始试样在加荷的过程中由于颗粒的破碎（即级配在变化）从一种级配材料逐渐变化成为了另外一种级配不同的材料。级配不同的试样都相应的对应某一临界状态，所以破碎程度不同的试样达到稳定状态时的临界状态就不相同。由图1的试验结果知，颗粒破碎轻微时临界状态线几乎与等向压缩线的初始段平行（因为等向压缩时应力水平较低，其颗粒破碎轻微，所以认为，等向固结线在e-lg p′平面中的斜率为常数），如果以颗粒不破碎时的临界状态线为基准（图1中的直线），那么找出其与颗粒破碎时的临界状态线的孔隙比的差值，就可以把颗粒破碎时在e-lg p′平面中呈曲线的临界状态线描述出来，式（1）可以描述堆石体颗粒破碎时在e-ln p′面上的临界状态线的变化。

2.2 状态参数

状态参数[12]ψ的定义如下

式中：e为当前的孔隙比。把式（2）代入式（1），得到

可见，通过状态参数的引入，把当前的状态与临界状态联系起来了。

2.3 本构方程

根据广义塑性理论，应力增量{dσ′}和应变增量{d}ε的关系为

式中：[D]ep为弹塑性刚度矩阵，可以表示为

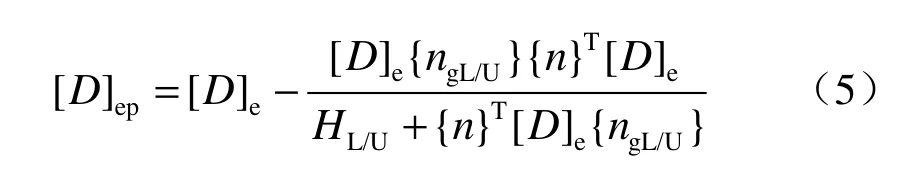
式中：[D]e为弹性刚度矩阵；{ngL/U}为塑性流动方向矢量；{n}为加载方向矢量；HL/U为塑性模量。下标L和U分别表示加载和卸载。

2.3.1 弹性特性

弹性特性由体变模量Kev和剪切模量Gev确定，对于堆石体，它们分别表示如下：

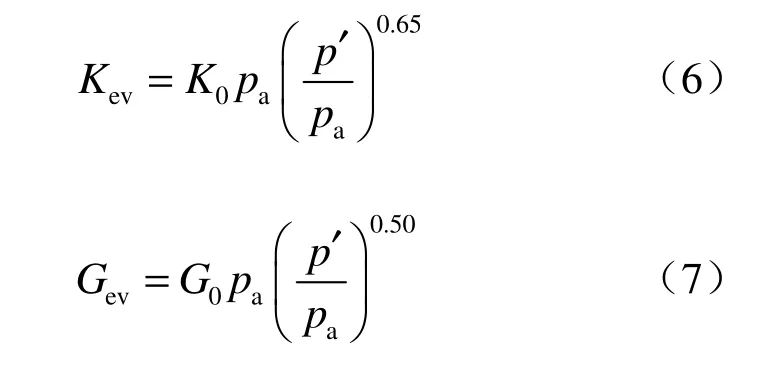
式中：pa为标准大气压（pa=101 kPa）；K0和G0材料常数。

2.3.2 剪胀

根据Li等[13]研究成果，此处对于堆石体采用如下的剪胀表达式：

式中：dg为剪胀比；Mg为q-p′面上临界状态线的斜率（尽管堆石体在q-p′面上呈非线性变化[15]，但考虑到把斜率取为常值变化不大，故此处取线性拟合的值）；η=q/p′为应力比；α和mg为常数。ψ=0和η=Md体变为0满足临界状态条件。对于初始较密的堆石体（ψ＜0），当η=Mgexp(mgψ′)达到相转换状态，其中ψ′为相转换状态上的ψ值。对于初始较松的堆石体（ψ＞0），当 Md＞Mg则相转换状态永远达不到。

2.3.3 塑性流动

塑性流动方向{ng}表示为

此处采用非相关联的流动法则，则加载方向{n}表示为

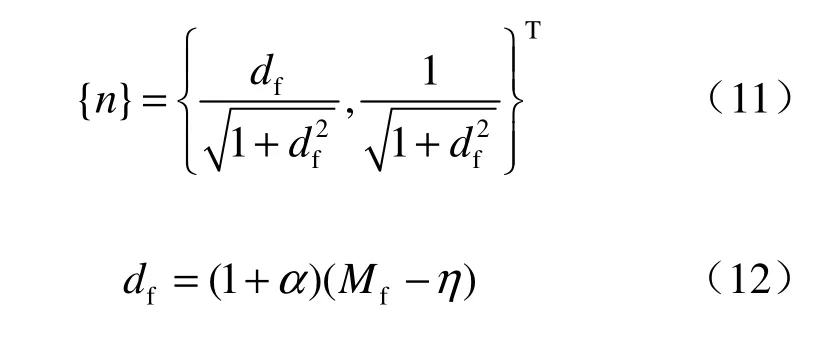
式中：Mf为常数。

2.3.4 塑性加载模量

此处对Ling等[12]对砂土的研究成果进行修正，得到堆石体在单调加载时的塑性加载模量如下：

式中：H0和m为常数；pc为固结完成时的平均有效应力，对于常规三轴试验即为固结完成时的平均应力。

从式（13）可以看出，塑性加载模量 HL的值取决于当前的应变力比η和临界状态线的斜率Mg的差值。当Mg＞η，H ＞0，硬化；Mg＜η，H ＜0，软化；Mg=η，H=0，峰值或破坏。

2.3.5 循环荷载作用时的塑性模量

（1）再加载模量

堆石体在排水条件下的试验结果表明，在卸荷时第1个循环内模量会减小很多，所以用弱化因数rβ来考虑这一影响。此外，排水条件下堆石体在循环荷载作用时会变得密实，此处用密实因数Hden来考虑这一影响。再加载模量表示为

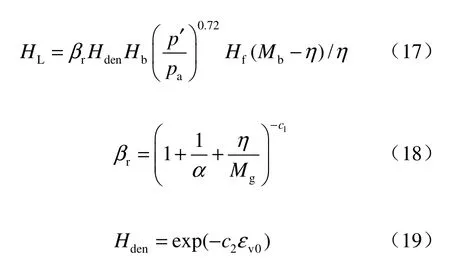
式中：c1和c2为常数；εv0为总的体积应变。相应的，Mb修改为下式

式中：β为正的参数；ζ为累积塑性剪应变；mb为常数。

（2）卸载模量

卸荷时产生塑性应变，体积是收缩的。因此，卸荷时的流动方向矢量表示为

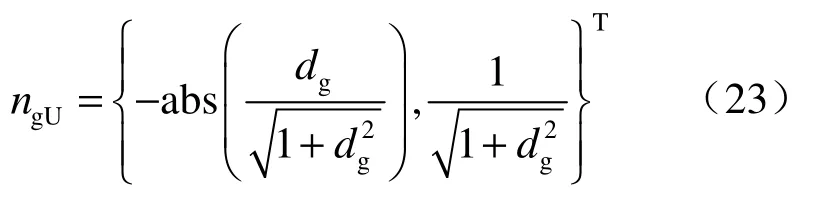
式中：abs表示求绝对值。

3 参数确定

以上提出的堆石体在循环加载下的本构模型具有18个模型参数，分为5组，分别是：与临界状态有关的参数eλ、λ、pci和ξ；弹性常数K0和G0；与剪胀有关的常数Mg、α和mg；与塑性流动有关的参数Mf；与塑性加载模量有关的参数H0和m；与再加载模量有关的常数c1、c2、β和mb；与卸载模量有关的常数HU0和mU。这些参数的具体确定方法如下。

3.1 临界状态参数

3.2 弹性常数

弹性常数K0可以从等向压缩试验得到；G0可以从应力-应变曲线得到，或者采用室内或室外的弹性波速试验测定。它们定义了堆石体的弹性行为。

3.3 剪胀参数

Mg为三轴试验q-p′面上临界状态线的斜率，由于堆石体在q-p′面上呈非线性变化，可以进行线性拟合得到。

mg可以通过在相转换状态时的排水或不排水试验确定，此时dg等于0，所以有下式：

式中：ηt和ψt为相转化状态时的η和ψ值。

3.4 塑性流动参数

Mf可以通过对不排水试验的应力路径（p′-q）或排水试验的体应变εv与轴向应变ε1关系曲线的拟合确定。

3.5 塑性加载模量参数

H0和m可以通过对不排水试验的应力路径（p′-q）或排水试验的体应变εv与轴向应变ε1关系曲线的拟合确定。

3.6 再加载模量参数

c1、c2、β和mb都是无量纲的常数，其中c1通过第1次再加载时的初始斜率确定或循环试验中的几次循环确定；c2通过排水时循环试验的应力-应变曲线形成的滞洄曲线确定；β通过循环试验的应力-应变曲线形成的滞洄曲线确定；mb通过循环试验的几次循环确定。

3.7 卸载模量参数

HU0和mU都是无量纲的常数，其中HU0可以通过第 1次卸载时的初始斜率确定；mU可以通过第1次卸载时的初始斜率确定或循环试验中的几次循环确定。

4 模型验证

采用提出的堆石体的动本构模型，对固结完成围压分别为400、800、1500、2200 kPa的循环荷载作用的堆石体的动三轴试验（试样尺寸为φ300 mm×750 mm，施加的轴向应力幅值为相应围压的 0.3倍）结果进行计算模拟，由试验得到的计算参数为：eλ=0.72、λ=0.027、ξ=0.12 和=1061.78 kPa；K0=5770.357 和G0=4228.787；Mg=1.293、α=0.45和mg=-0.2994；Mf=1.450；H0=11111 和m=-1.05；c1=-1.9、c2=18.5、β=28.5和mb=0.76；HU0=7.5×106和mU=4.2。图2～5为试验结果与模拟结果的对比。

计算与试验结果的对比表明，采用本文建议的动本构模型可以模拟堆石体在循环荷载作用下的主要变形特征[1]，包括动残余变形、应力循环过程中的变形特性、高应力水平时颗粒破碎引起的体缩。循环荷载作用下（应力幅值为围压的0.3倍），围压低时残余体变和剪应变较小，而围压高时残余体变和剪应变较大。在一应力循环中，围压高时应力引起的应变变化范围较大，而围压低时应力引起的应变变化范围较小，表明围压高时颗粒破碎导致的残余体变较大。但由于堆石体在循环荷载作用下力学性质的复杂性，还需要开展更深入的研究来描述颗粒破碎下其动应力-应变关系。

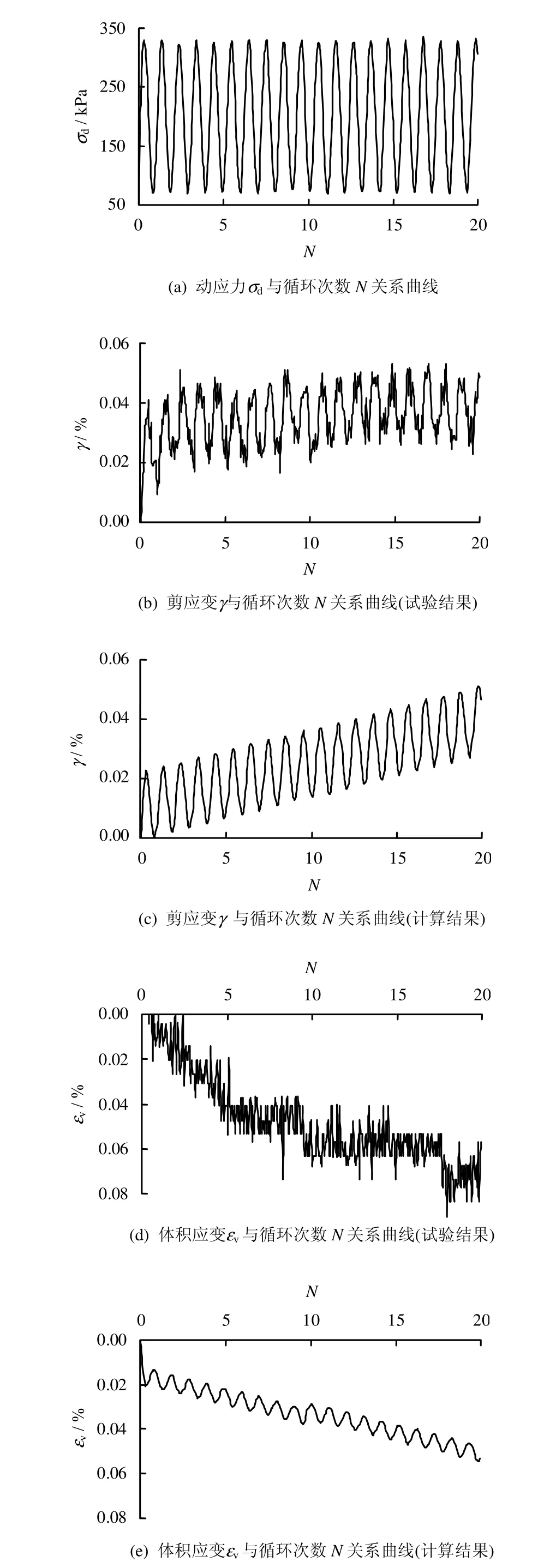
图2 计算与试验结果对比（σc=400 kPa）Fig.2 Comparisons between calculated and tested results（σc=400 kPa）

图3 计算与试验结果对比（σc=800 kPa）Fig.3 Comparisons between calculated and tested results（σc=800 kPa）

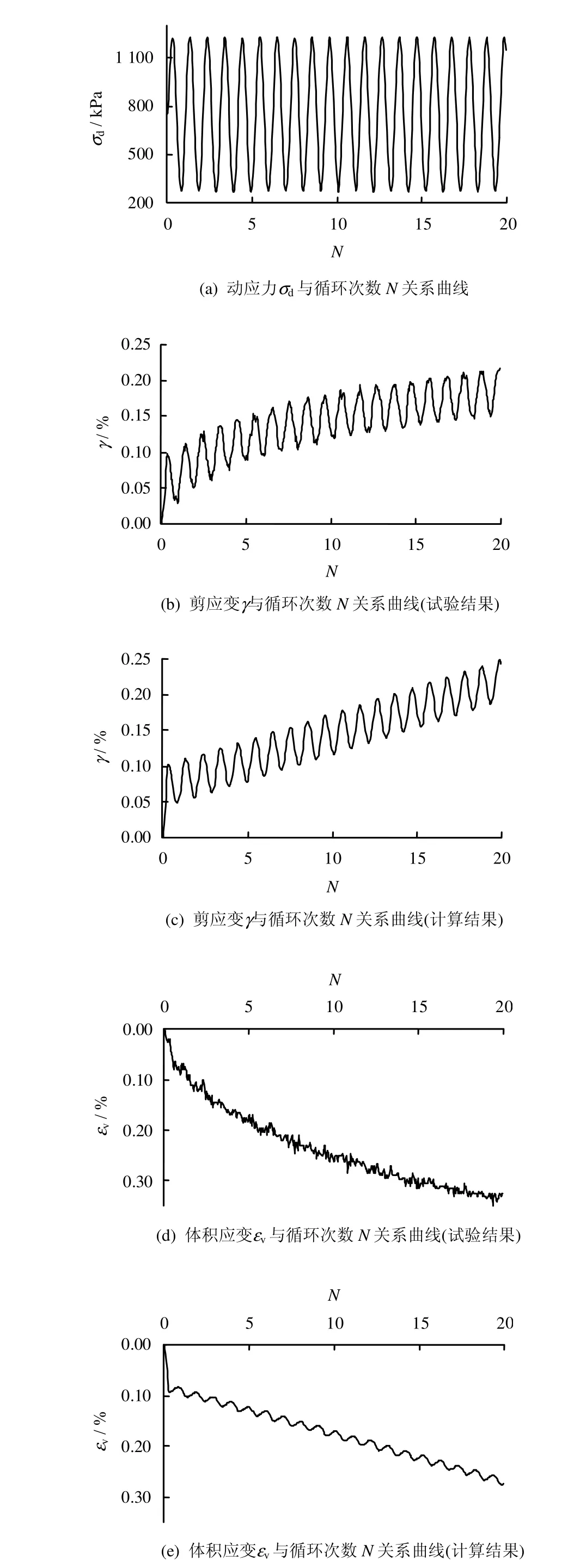
图4 计算与试验结果对比（σc=1500 kPa）Fig.4 Comparisons between calculated and tested results（σc=1500 kPa）

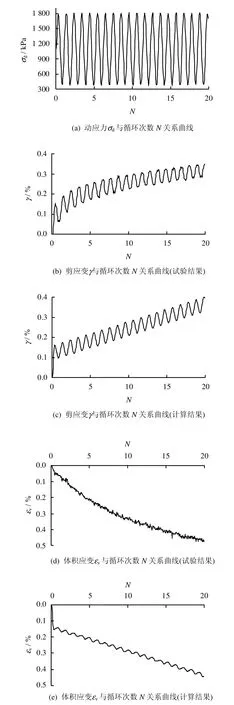
图5 计算与试验结果对比（σc=2200 kPa）Fig.5 Comparisons between calculated and tested results（σc=2200 kPa）

5 结 论

（1）基于堆石体在循环荷载作用下的动应力应变特点和堆石体在q-p′平面和e-lg p′平面上临界状态线均为非线性变化，通过引入状态参数，提出了一个考虑颗粒破碎的堆石体的动本构模型。

（2）通过与堆石体的动三轴试验结果的对比表明，所建议的动本构模型可以模拟堆石体在循环荷载作用下的动残余变形、应力循环过程中的变形特性和高应力水平时颗粒破碎引起的体缩等主要变形特性。

[1]陈生水,韩华强,傅华. 循环荷载下堆石料应力变形特性研究[J]. 岩土工程学报,2010,32(8): 1151－1157.CHEN Sheng-shui,HAN Hua-qiang,FU Hua. Stress and deformation behaviours of rockfill under cyclic loadings[J]. Chinese Journal of Geotechnical Engineering,2010,32(8): 1151－1157.

[2]NAKATA Y,HYDE A F L,HYODO M,et al. A probabilistic approach to sand particle crushing in the triaxial test[J]. Geotechnique,1999,49(5): 567－583.

[3]COOP M R,SORENSEN K K,FREITAS T B,et al.Particle breakage during shearing of a carbonate sand[J].Geotechnique,2004,54(3): 157－163.

[4]YASUDA N,MATSUMOTO N,YOSHIOKA R,et al.Undrained monotonic and cyclic strength of compacted rockfill material from triaxial and torsional simple shear tests[J]. Canadian Geotechnical Journal,1997,34(3):357－367.

[5]沈珠江,徐刚. 堆石料的动力变形特性[J]. 水利水运科学研究,1996,(2): 143－150.SHEN Zhu-jiang,XU Gang. Dynamic deformational properties of rockfill materials[J]. Hydro-Science and Engineering,1996,(2): 143－150.

[6]陈生水,沈珠江,丽能惠. 复杂应力路径下无黏性土的弹塑性数值模拟[J]. 岩土工程学报,1995,17(2):20－28.CHEN Sheng-shui,SHEN Zhu-jiang,LI Neng-hui. An elasto-plastic model for cohesionless soils under complex stress paths[J]. Chinese Journal of Geotechnical Engineering,1995,17(2): 20－28.

[7]SHEN Zhu-jiang. A granular medium model for liquefaction analysis of sands[J]. Chinese Journal of Geotechnical Engineering,1999,21(6):742－748.沈珠江. 砂土液化分析的散粒体模型[J]. 岩土工程学报,1999,21(6):742－748.

[8]DAFALIAS Y F. Bounding surface plasticity I:Mathematical foundation and hypoplasticity[J]. Journal of Engineering Mechanics,ASCE,1986,112(9): 966－987.

[9]WANG Z L,DAFALIAS Y F,SHEN C K. Bounding surface hypoplasticity model for sand[J]. Journal of Engineering Mechanics,ASCE,1990,116(5): 983－1001.

[10]吴兴征,栾茂田,李相崧. 复杂加载路径下堆石料动力本构模型及数值模拟[J]. 世界地震工程,2001,17(1): 9－14.WU Xing-zheng,LUAN Mao-tian,LI Xiang-song.Bounding surface hypoplastic model for rockfill materials under complex loading paths and its verification[J].World Information on Earthquake Engineering,2001,17(1): 9－14.

[11]PASTOR M,ZIENKIEWICZ O C,CHAN A H C.Generalized plasticity and the modeling of soil behavior[J]. International Journal for Numerical and Analytical Methods in Geomechanics,1990,14(3): 151－190.

[12]LING H I,YANG S. Unified sand model based on the critical state and generalized plasticity[J]. Journal of Engineering Mechanics,ASCE,2006,132(12): 1380－1391.

[13]LI X S,DAFALIAS Y F. Dilatancy for cohesionless soils[J]. Geotechnique,2000,52(3): 173－186.

[14]周成,沈珠江,陈生水,等. 次塑性模型及饱和砂土动力弹塑性响应分析[J]. 岩土力学,2004,25(4): 549－554.ZHOU Cheng,SHEN Zhu-jiang,CHEN Sheng-shui,et al.Hypoplasticity model and analysis of dynamic elastoplastic response of saturated sand[J]. Rock and Soil Mechanics,2004,25(4): 549－554.

[15]刘恩龙,陈生水,李国英,等. 堆石料的临界状态与考虑颗粒破碎的本构模型[J]. 岩土力学,2011,32(增刊2):148－154.LIU En-long,CHEN Sheng-shui,LI Guo-ying,et al.Critical state of rockfill materials and a constitutive model incorporating grain crushing[J]. Rock and Soil Mechanics,2011,32(Supp.2): 148－154.