反倾岩质边坡悬臂梁极限平衡模型的改进

卢海峰，刘泉声,，陈从新

（1.武汉大学 土木建筑工程学院，武汉 430072；2.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室，武汉 430071）

1 引 言

反倾岩质边坡的研究已有近 30多年的历史，20世纪70年代，Goodman等[1]最早提出了基于极限平衡原理的分析方法，此方法将倾倒体离散为若干倾斜的矩形条块，根据静力平衡条件分析边坡倾倒的危险性。90年代，陈祖煜等[2]对Goodman-Bray方法进行了改进和简化。韩贝传等[3]从边坡倾倒的变形特点出发，通过有限元计算分析了倾倒变形的力学机制。程东幸等[4]借助广西龙滩水电站左岸边坡工程地质剖面模型以及岩体参数，通过离散元程序3DEC对反倾岩质边坡的影响因素进行了多工况分析，提出了边坡反倾优势角的范围。Aydan等[5]采用悬臂梁弯曲模型，应用极限平衡理论，通过迭代求解得到反倾边坡坡脚剩余下滑力，建立了通过剩余下滑力判断边坡稳定性评价方法，并通过室内底摩擦模型试验进行了验证。Adhikary和 Dyshin等[6－7]分别在 1997年和 2007年通过试验对 Aydan和Kawamoto的研究理论进行了完善和推广。在反倾层状岩体弯曲-拉裂破坏模式的分析和研究方面，许多学者也进行了相关的研究并取得了相应的成果，如文献[8－10]。

反倾岩质边坡稳定性及破坏机制研究一直以来是边坡稳定性分析中的难点，有很多悬而未决的问题。极限平衡分析方法仍然是目前最为常用的一种方法，也是相对比较成熟的一种方法。本文借助悬臂梁弯曲模型的极限平衡分析方法，在对其进行合理改进的基础上，提出了采用剩余不平衡力对反倾边坡稳定性影响因素进行探讨分析，得出相应结论，对该类边坡的设计施工具有指导意义。

2 理论背景介绍

层状岩石边坡弯曲倾倒本质上是由于弯曲引起的拉应力在岩柱最大弯矩点产生拉裂缝造成的。全面系统地计算边坡岩体的弯矩是非常复杂的，因此，Aydan等[5]提出运用极限平衡方法分析此类问题，Adhikary等[6]在此基础上进行了改进（模型如图1(a)所示）。

图1 悬臂梁极限平衡受力图（Adhikary等[6]）Fig.1 Free-body diagram of cantilever beam limit equilibrium model (Adhikary, et al[6])

理论模型建立的基础基于以下几点假定：每层岩层或岩柱可以看做是在自重力和边界力作用下的悬臂梁（如图1所示）。为了简化计算，将边界上的力简化成集中力，作用点位于χhj处，其中hj为所研究岩柱段的长度，j为研究岩层的编号，χ ∈(0,1)是表征层间作用力作用点与所考虑岩柱位置关系的系数。边坡岩体中存在一个基准面，所有基准面以上岩层同时处于极限平衡状态。在极限平衡状态下，作用在基准面上的最大拉应力（=b /2）等于岩层材料的抗拉强度（σt），基准面为沿与层面法线方向呈θ角斜向上的平面（如图1(a)）。在上述假定条件的基础上，岩层可以看作是在重力、侧力以及弯矩作用下的梁或柱。在上述力和弯矩作用下，梁或柱在平面应变状态下距中轴线距离为y处的轴向应力σx满足以下关系式：

式中：N为轴力；M为弯矩；A为岩柱的截面积；I为极惯性矩。

以式（1）为基础，代入图1(b)所示的力，Aydan等[5]推导出了以下表达式：

在式（2）的基础上，从边坡上部在自重力作用下不稳定的岩层开始到坡脚岩层，采用迭代计算方法对边坡岩层进行计算分析。每一步迭代得到的Pj-1的值作为下一步迭代计算式中Pj，直到最终计算得到坡脚处的剩余不平衡力 P0。然而实际的边坡坡脚没有力来维持这点平衡，所以 P0的值可以作为判断边坡稳定性的一项指标：P0＞0时，边坡不稳定；P0=0时，处于极限平衡状态；P0＜0时，边坡稳定。

3 模型讨论

在Goodman和Bray提出的极限平衡分析方法基础上，由Aydan和 Kawamoto以及Adhikary和Dyskin建立的悬臂梁极限平衡迭代模型能够简洁直观地对反倾岩质边坡稳定性作出分析评价，尤其是对岩性较软，以弯曲-倾倒破坏为主的边坡，该模型更为合理。通过对模型建立过程及假设条件的详细解读，结合边坡实际破坏过程，笔者认为，该模型建立和简化过程中有些问题与该类边坡的实际破坏模式有一定出入，有待进一步探讨和商榷，主要问题可以概括为以下几点：

①模型假定边坡中存在从坡脚延伸至坡顶的基准面，该面与层面法线方向呈θ角斜向上，面上所有块体达到极限平衡状态。最初，在 Aydan和Kawamoto模型中θ=0，后来 Adhikary和 Dyskin通过试验得出θ的合理范围在12°～20°。然而，实际的反倾边坡破坏断裂面并不是理想的直线型，断裂面以上块体也并不是同时达到极限平衡状态。

②模型迭代计算起始岩层为边坡上部在自重力作用下不稳定的岩层。然而模型中对于该起始岩层如何确定没有给出判断标准，而是以直线破裂面延伸至坡顶最远处的岩层。笔者认为，这个假定的合理性有待商榷，既然模型中定义起始不稳定岩层是在自重作用下不稳定的块体，那么就应该以只有自重力作用下的岩层稳定分析来判断该起始层，而且实际边坡中显示该起始不稳定位置的张裂缝往往也不会延伸到坡顶后面很远的位置，有的甚至在坡面上出现。

③无论是 Aydan和 Kawamoto的模型，还是Adhikary和Dyskin模型，层间剪切力都只考虑了层间内摩擦角φ的影响，而没有考虑层间凝聚力 c。Adhikary和Dyskin在2007年的研究中指出，层间凝聚力c只要满足允许层间滑动的前提条件即可，对边坡失稳机制的影响没有层间内摩擦角φ的影响大。上述模型迭代中均没有考虑凝聚力c的作用，可能是由于模型建立时认为各部分岩层层间已经发生错动，层间作用以摩擦为主。笔者认为，破裂面上并不是所有的岩层都同时发生层间错动，而且Adhikary和 Dyskin也在研究中提到凝聚力对层间错动的影响，尤其是软岩和黏土岩类层面，本身凝聚力在层间剪切力中所占的比例较大，其对层间错动和整个边坡破坏模式的影响就更不能忽视。

④模型迭代式中对于岩层厚度、内摩擦角等因素均按不同层位分别考虑，对于岩层重度γ却没有区别对待。虽然这部分对边坡破坏模式及稳定性影响可能不是很大，但对于岩层重度差异较大，尤其是软硬岩互层的边坡，该部分影响还是应该考虑，所以模型中的岩层重度还是应该分别考虑各层重度γj。

4 模型改进

以上针对Adhikary和Dyskin模型中存在的问题进行了讨论，认为破裂面的形式、起始不稳定层的确定、层间凝聚力的影响以及重度分层等方面问题需要进一步探讨，因此，在 Adhikary和 Dyskin模型的基础上，采用合理的分析处理方法，对上述几方面问题进行了修正和改进，提出了新的悬臂梁极限平衡迭代分析模型。

4.1 破裂面和起始不稳定层位修正

第3节分析中已经指出，起始不稳定层是在自身重力作用下不稳定的岩层。对于某一独立岩层，在其自重作用下的弯曲折裂面应该位于岩层内拉应力等于岩层材料抗拉强度的位置，基于这一思想，可以求出岩层在自重作用下失稳的临界长度。

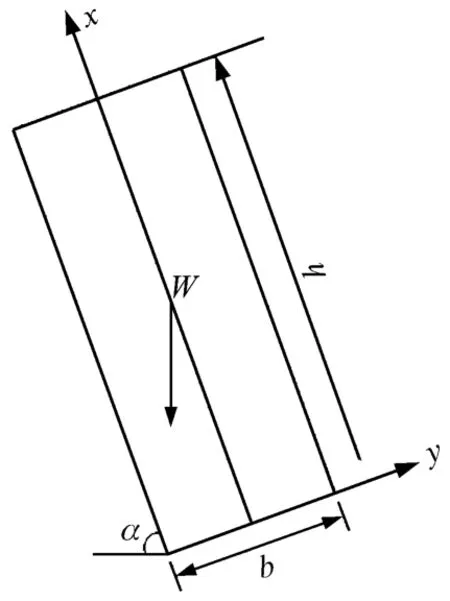
图2 临界失稳长度分析图Fig.2 Analysis chart of critical instability length

如图2所示，岩层厚度为b，倾角为α的单层岩层在自重作用下的临界失稳长度为 h，则在临界弯折点(0,b/2)处满足最大拉应力等于岩层抗拉强度值，即

而根据力的平衡关系得出该点处：

联立式（3）、（4），代入各表达式得到临界失稳长度h的求解方程为

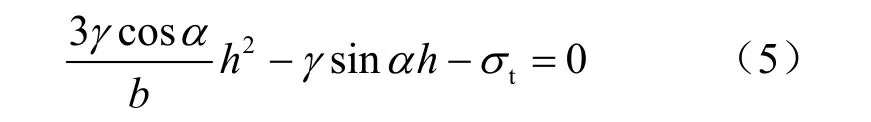
由于h＞0，根据式（5），解方程得到单一岩层临界失稳长度h的求解表达式为

以b=10 m，α=60°，γ=25 kN/m3，σt=1 MPa的等厚岩层模型为例，结合上述临界失稳长度分别对Aydan模型基准面和Adhikary模型基准面进行分析，在此基础上提出了改进的基准面确定方法（如图3所示）。

根据式6计算得出岩层自重作用下临界失稳长度h=19.5 m，在图中分别标出各层临界断裂面的位置（如图3所示）。从图中可以看出，大部分岩层（编号 5～14）在自重条件下的临界断裂面位于 Aydan基准面之上，可见在这种边坡模型下，很多岩层断裂面位置并未到达预定断裂面；Adhikary基准面情况下，许多岩层自重条件下的临界断裂面都位于Adhikary基准面之下，说明该基准面模式下岩层在自重条件下是比较稳定的，破坏主要是由于岩层之间相互作用引起的。

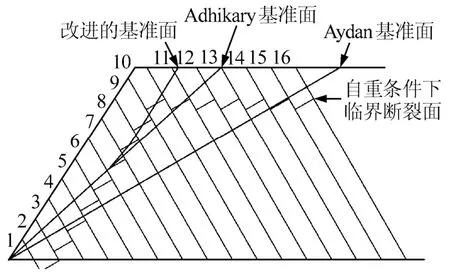
图3 折裂面改进分析图Fig.3 Analysis chart of improved fracture plane

综合两种基准面与自重条件下的临界断裂面之间的关系，笔者认为，边坡弯曲倾倒破坏模式基准面可以分为两部分来考虑，一部分是边坡上部倾倒区；另一部分是边坡下部滑移区。这点在Goodman 和 Bray块体极限平衡分析计算中也能体现出来。上部倾倒区主要以自重作用下临界断裂面为判断依据，而下部滑移区主要以Adhikary基准面为依据。基于上述思想，对悬臂梁极限平衡模型分析中断裂面进行改进，具体方法如下：

（1）根据边坡模型尺寸及参数，运用式（6）计算得到各层自重作用下的临界断裂长度，并在图上画出各层临界断裂面位置；

（2）在图中画出Adhikary基准面，从坡脚岩层往上找到该基准面与临界断裂面相交的岩层，并以此为基准面折断点；

（3）从上述折断点开始，向坡顶方向依次连接各层临界断裂面中点，并延伸至坡顶，该部分断裂面和下部原 Adhikary断裂面共同组成改进的基准面（如图3所示）。

4.2 层间凝聚力c和重度γ 修正

前面在 Adhikary模型的基础上对基准面的形式进行了改进，下面将在原迭代公式的基础上对层间凝聚力c和分层重度γ进行修正。原模型中力学平衡关系没有变化，只是层间剪切力的计算中应该加入凝聚力c值，即：

在Aydan 和Kawamoto推导理论的基础上，代入式（7），同时将模型中的重度γ分别用各层重度jγ，可以得到修正的悬臂梁极限平衡模型迭代表达式为

5 基于改进模型的反倾岩质边坡稳定性影响因素分析

潘家铮[11]“最大值原理”指出：滑坡体的滑面确定时，则滑面上的反力（以及滑坡体内的内力）能自行调整，以发挥最大的抗滑能力。无论是Adhikary模型，还是改进的模型，迭代计算过程都是遵循这一原理，所得到的各层剩余不平衡力Pj反映了各层相互作用维持极限平衡状态所需的反力的大小，然而实际岩层之间并不存在这一反力，因此，该力Pj的大小实际反映了岩层的稳定情况：Pj＞0说明该处岩层要维持平衡还需要施加外力作用，因此，在实际没有外力作用的情况下，该处岩层是不稳定的；Pj＜0说明不仅不需要外力维持平衡，而且还有一定的储备来抵抗外力作用，因此，该段是稳定的；Pj=0则正好处于极限平衡状态。基于上述思想，考虑利用改进的悬臂梁极限平衡模型，通过迭代计算得到的Pj值的大小来评价分析反倾边坡稳定性的影响因素。

5.1 边坡坡角影响分析

前面分析中已经提到，改进模型的基准面在坡脚起始段位于岩层层面法平面上部，并与法平面呈θ角（如图6所示），位于基准面以上的岩层才有可能发生失稳破坏。因此，边坡坡角与岩层倾角满足一定关系才有可能发生破坏。

根据图6所示关系可以得出，反倾岩质边坡满足式（9）所示的关系才有可能发生失稳破坏，即：

式中：β为边坡开挖坡角；α为岩层倾角；θ为Adhikary基准面与层面法平面夹角，一般取12°～20°。

在上述关系式的基础上，以岩层倾角α=60°的边坡为例来研究坡角变化对反倾岩质边坡稳定性的影响。依据式（9），取θ=12°，则α=60°，则边坡发生失稳破坏的坡角下限值为42°，设计边坡坡角分别为 50°、60°和 70°的3种模型，按照改进的悬臂梁极限平衡模型方法，先确定不同坡角下的边坡稳定性分析基准面，然后再根据改进的迭代式进行计算分析。计算模型及各坡角情况下的基准面如图7所示，在上述模型基础上，选取适当参数，运用式（8）迭代计算，分别得到3种坡角情况下的剩余不平衡力分布，如图8所示。从图中可以看出，坡角β=50°时，边坡岩层全部处于稳定状态（ Pj＜0）；当坡角增大到 60°时，边坡 3～7号岩层处于不稳定状态（ Pj＞ 0），同时坡脚 1～2号岩层处于稳定抗滑段（ Pj＜0），而且Pj很小，具有比较高的安全储备；当坡角增大到70°时，边坡2～5号岩层都处于不稳定状态（ Pj＞ 0），只有坡脚处1号岩体处于稳定抗滑段，但其值已经接近极限状态，抗滑作用也大大减弱。

图6 坡角与岩层倾角关系图Fig.6 Relationship between dip angle and slope angle

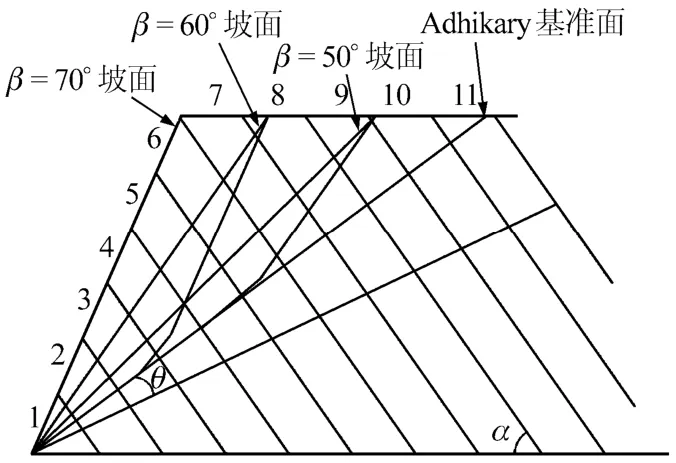
图7 不同坡角边坡计算模型图Fig.7 Computational model chart of different slope angles

图8 不同坡角剩余不平衡力分布图Fig.8 Distribution chart of residual unbalanced force under different slope angles

可见，在满足反倾岩质边坡失稳下限坡角条件下，随着边坡坡角的增大，其不稳定区所涉及到的岩层数量逐渐减少，但不稳定区域范围逐渐向坡脚发展，且坡脚抗滑段的抗滑能力逐渐减弱。

5.2 岩层倾角影响分析

为了研究岩层倾角变化对反倾岩质边坡稳定性的影响，以坡角β=60°的边坡为例，按照上节同样的方法对边坡进行计算分析。根据式（6）、（9）所示关系，岩层倾角必须大于42°边坡才有可能发生破坏，因此，分别取岩层倾角为 50°、60°和70°。

计算模型及各岩层倾角情况下的基准面如图 9所示，根据计算模型，运用式（8）迭代计算，分别得到3种岩层倾角情况下的剩余不平衡力分布，如图10所示。从图中可以看出，岩层倾角变化对岩层剩余不平衡力的影响与坡角变化的影响类似，随着岩层倾角的增大，不稳定岩层区域逐渐向坡脚岩层移动，且坡脚岩体的抗滑储备逐渐减小。

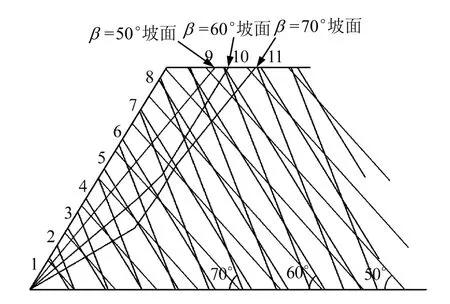
图9 不同岩层倾角计算模型图Fig.9 Computational model chart of different dip angles

图10 不同岩层倾角剩余不平衡力分布图Fig.10 Distribution chart of residual unbalanced force under different dip angles

5.3 边坡高度影响分析

为了研究边坡高度对反倾边坡稳定性的影响，以坡角β=60°，岩层倾角α=60°的边坡为例，对不同高度边坡模型进行迭代计算分析，得到各岩层剩余不平衡力分布图（如图12所示）。从图中计算结果可以看出，随着H的增大，边坡不稳定区域的范围逐渐增大，且不稳定区不平衡力也逐渐增大，说明随着边坡高度的增加，边坡不稳定性逐渐增加，但坡脚处抗滑段区域的大小和抗滑区安全储备几乎不受坡高的影响，可见仅边坡高度增加会影响边坡不稳定岩层的范围，但对抗滑区的范围及安全储备影响不太明显。

图11 不同坡高计算模型图图Fig.11 Computational model chart of different slope heights

图12 不同坡高剩余不平衡力分布图Fig.12 Distribution chart of residual unbalanced force under different slope heights

从计算结果图中可以看出，当模型未退化到Adhikary基准面以前，随着抗拉强度的增加，不稳定区的范围有所增大，且不稳定区岩层的不平衡力也有所增大，但坡脚抗滑段的安全储备也随之增大，这是因为在退化到Adhikary基准面以前，抗拉强度不仅影响计算迭代值的大小，同时还影响基准面的形态。当模型退化到Adhikary基准面以后，随着抗拉强度的增加，岩层不稳定区的范围减小，当σt=0.4 MPa，所有岩层均进入稳定阶段。总体来看，无论是退化前还是退化后，坡脚抗滑段安全储备都随抗拉强度的增加而增大。

5.4 岩层抗拉强度的影响分析

在改进的悬臂梁极限平衡模型计算中，岩层抗拉强度一方面影响单一岩层临界失稳长度 h（如式6），从而影响计算基准面的形态；另一方面作为迭代计算参数也将影响计算结果。以坡角β=60°，岩层倾角α=60°的边坡为例，分别取岩层抗拉强度为0.1、0.2、0.3、0.4 MPa进行计算分析，计算模型及各抗拉强度下的计算基准面如图13所示。从模型图中可以看出，当抗拉强度增大到0.3 MPa时，由于单一岩层临界失稳长度h已经超过原Adhikary基准面上所有岩层的长度，本文对于这种情况下的基准面采取退化到Adhikary基准面的处理方式，这样计算得到结果是偏于安全的。因此，图中σt=0.3 MPa和σt=0.4 MPa时的基准面均采用Adhikary基准面进行计算分析。通过改进模型迭代式计算，得到不同抗拉强度下剩余不平衡力分布图（如图14所示）。

图13 不同抗拉强度计算模型图Fig.13 Computational model chart of different tensile strengths

图14 不同抗拉强度剩余不平衡力分布图Fig.14 Distribution chart of residual unbalanced force under different tensile strengths

5.5 层间内摩擦角和凝聚力的影响分析

反倾岩质边坡岩层在自重作用下首先达到自平衡，当自重条件不能满足平衡时，就会发生层间作用，各岩层之间相互作用，以发挥边坡的最大抗滑作用。在这个过程中，层间内摩擦角和凝聚力起到十分重要的作用。层间内摩擦角和凝聚力对模型计算基准面没有影响，所以选取坡角β=60°，岩层倾角α=60°的边坡为例（如图15所示），分别对内摩擦角φ=10°、20°、30°和40°以及凝聚力c=0、100、500、1000 kPa的边坡模型进行计算，研究其对边坡稳定性的影响，具体计算结果分别如图16、17所示。

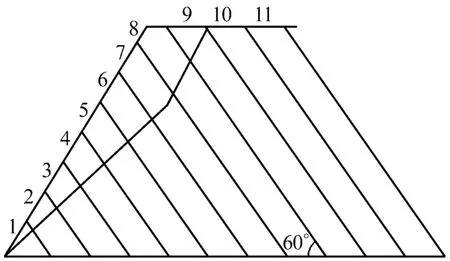
图15 层间内摩擦角及凝聚力影响计算模型Fig.15 Computational model chart of internal friction angle and cohesion

图16 不同层间凝聚力剩余不平衡力分布图Fig.16 Distribution chart of residual unbalanced force under different cohesions

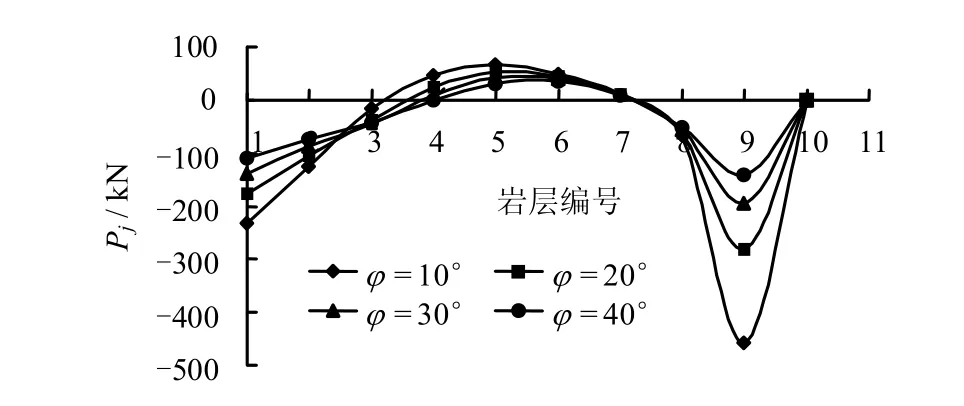
图17 不同层间内摩擦角剩余不平衡力分布图Fig.17 Distribution chart of residual unbalanced force under different internal friction angles

从图中可以看出，层间凝聚力c值对岩层不平衡力的大小和分布的影响比较明显，当c值从1 MPa降低到 0时，各层岩层也从全部处于稳定状态（Pj＜0）逐渐出现不稳定区，随着c值的降低，不稳定区的范围和剩余不平衡力的大小都逐渐增加。随着层间内摩擦角的增大，边坡不稳定区的范围逐渐减小，这点与前面层间凝聚力的影响规律是一致的。两者对边坡坡脚抗滑段的影响有所区别：随着层间内摩擦角的增大，坡脚抗滑段的安全储备逐渐降低；而层间凝聚力的影响正好相反，即随着层间凝聚力的增加，坡脚抗滑段的安全储备逐渐增加。笔者认为，这种差异反映了两者对边坡破坏过程的影响机制不同，层间凝聚力对岩层的影响与作用在层间的力的大小无关，一旦边坡几何形态确定，它对边坡的影响程度也就确定了，对各部分岩层的影响规律是一致的；而层间内摩擦角对边坡稳定性的影响与层间作用力有关，层间内摩擦角越小，岩层之间相互作用越弱，各岩层自身不平衡力通过层间错动消耗，随着内摩擦角的增加，层间相互协调作用能力增大，处于不平衡区的岩层可以调动更多的岩层相互作用来分担自身的不平衡力，所以内摩擦角越大，不稳定区的范围减小，且坡脚抗滑区的安全储备也随之减小，这正是各岩层之间相互协调作用的结果。

6 结 论

（1）边坡坡角β和岩层倾角α必须满足β＞(90°-α+)θ这一基本关系式才有可能发生失稳破坏，其中θ为Adhikary模型中基准面与岩层法平面夹角，一般在12°～20°之间。

（2）岩层倾角变化对岩层剩余不平衡力的影响与坡角变化的影响类似，随着两者角度值的增大，不稳定岩层区域逐渐向坡脚岩层移动，且坡脚岩体的抗滑储备逐渐减小。

（3）边坡高度对边坡稳定性的影响主要体现在对不稳定区域的范围和不稳定区不平衡力的影响：高度越大，不稳定区范围和不平衡力也越大。对坡脚处抗滑段区域大小和抗滑区安全储备影响不大。

（4）岩层抗拉强度对边坡的影响一方面是对计算基准面形态的影响，另一方面也将影响不平衡力计算结果。当模型未退化到Adhikary基准面以前，随着抗拉强度的增加，不稳定区的范围有所增大，且不稳定区岩层的不平衡力也有所增大，但坡脚抗滑段的安全储备也随之增大；当模型退化到Adhikary基准面以后，随着抗拉强度的增加，岩层不稳定区的范围减小，最终所有岩层均进入稳定阶段。无论是退化前还是退化后，坡脚抗滑段安全储备都随抗拉强度的增加而增大。

（5）随着层间内摩擦角和凝聚力的增大，边坡不稳定区的范围均减小。但对坡脚抗滑段的影响，层间内摩擦角和凝聚力影响规律正好相反：随着层间内摩擦角的增大，坡脚抗滑段的安全储备逐渐降低；随着层间凝聚力的增加，坡脚抗滑段的安全储备逐渐增加。

通过综合分析可以看出，反倾岩质边坡中部一般最先出现不稳定区，而坡脚为整个边坡的抗滑段，坡角、岩层倾角等各因素主要影响不稳定区的分布和坡脚抗滑段的安全储备，层间内摩擦角和层厚对于各岩层之间相互协调、共同作用有一定影响。基于改进的悬臂梁极限平衡模型对边坡稳定性及影响因素的分析，比较合理地反应了现场边坡破坏的实际机制，对设计和施工具有一定的指导意义，尤其是提出的模型改进折裂面确定方法值得进一步深入推广研究。

[1] GOODMAN R E, BRAY J W. Toppling of Rock Slopes[C]//Proceedings of the Speciality Conference on Rock Engineering for Foundations and Slopes. Bouider:ASCE, 1976.

[2] 陈祖煜, 张建红, 汪小刚. 岩石边坡倾倒稳定分析的简化方法[J]. 岩土工程学报, 1996, 18(6): 92－95.

[3] 韩贝传, 王思敬. 边坡倾倒变形的形成机制与影响因素分析[J]. 工程地质学报, 1999, 7(3): 213－217.HAN Bei-chuan, WANG Si-jing. Mechanism for toppling deformation of slope and analysis of influencing factors on it[J]. Journal of Engineering Geology, 1999, 7(3):213－217.

[4] 程东幸, 刘大安, 丁恩保, 等. 层状反倾岩质边坡影响因素及反倾条件分析[J]. 岩土工程学报, 2005, 27(11):1362－1366.CHENG Dong-xing, LIU Da-an, DING En-bao, et al.Analysis of influential factors and toppling conditions of toppling rock slope[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(11): 1362－1366.

[5] AYDAN O, KAWAMOTO T. The stability of slopes and underground openings against flexural toppling and their stabilization[J]. Rock Mechanics and Rock Engineering,1992, 25(3): 143－165.

[6] ADHIKARY D P, DYSKIN A V, et al. A study of the mechanism of flexural toppling failure of rock slopes[J].Rock Mechanics and Rock Engineering, 1997, 30(2):75－93.

[7] ADHIKARY D P, DYSKIN A V. Modelling of progressive and instantaneous failures of foliated rock slopes[J]. Rock Mechanics and Rock Engineering,2007, 40(4): 349－362.

[8] 蒋良维, 黄润秋. 反倾层状岩体斜坡弯曲-拉裂两种失稳破坏之判据探讨[J]. 工程地质学报, 2006, 14(3): 289－295.JIANG Liang-wei, HUANG Run-qiu. Bending yielding and tensile cracking criteria for failure of rock slope whose dip direction opposite to the dip direction of strata[J]. Journal of Engineering Geology, 2006, 14(3):289－295.

[9] 陈红旗, 黄润秋. 反倾层状边坡弯曲折断的应力及挠度判据[J]. 工程地质学报, 2004, 12(3): 243－246.CHEN Hong-qi, HUANG Run-qiu. Stress and flexibility criteria of bending and breaking in a countertendency layered slope[J]. Journal of Engineering Geology, 2004,12(3): 243－246.

[10] 伍法权. 云母石英片岩斜坡弯曲倾倒变形的理论分析[J].工程地质学报, 1997, 5(4): 306－311.WU Fa-quan. Theoretical analysis of bending and toppling deformation in slopes of mica-quartz schist[J].Journal of Engineering Geology, 1997, 5(4): 306－311.

[11] 陈祖煜. 土质边坡稳定分析[M]. 北京: 中国水利水电出版社, 2003.