笛卡尔坐标系在数控机床中的应用

张国政 杨海卉

（安徽机电职业技术学院，芜湖 241000）

笛卡尔坐标系在数控机床中的应用

张国政 杨海卉

（安徽机电职业技术学院，芜湖 241000）

右手直角笛卡尔坐标系是数控机床的标准坐标系。以此坐标系来判别数控机床的空间几何关系以及加工过程需建立的刀具半径左、右补偿，刀具的刀尖方位和数控加工中的顺逆圆弧方式，并总结出相关实用规则。旨在说明笛卡尔坐标系的实际应用，指出数控加工人员的一些判别误区。

笛卡尔坐标；数控机床；坐标轴判别；刀具位置

直角笛卡尔坐标系是17世纪法国数学家勒奈·笛卡尔提出的。这一坐标系在设计、绘制和数字控制等领域已有四百多年历史，自上个世纪50年代美国第一台三坐标数控铣床的诞生，发展至现代的多轴联动高性能数控机床，一直以右手直角笛卡尔坐标系作为标准坐标系。文中通过笛卡尔坐标系可确定数控机床各坐标轴空间几何关系及加工过程中的刀具位置关系。

1 数控机床的空间几何关系

数控机床的空间几何关系是机床固定点和工件浮动点之间距离的关系，一般采用右手坐标系确定，坐标轴的正负向由确定的视图转换来决定［1］，如图 1所示。图中的 X、Y、Z、A、B、C 分别表示机床运动过程中，假定刀具相对于静止的被加工工件的坐标，并规定刀具远离工件的方向为正方向(计为“规则 1”)。

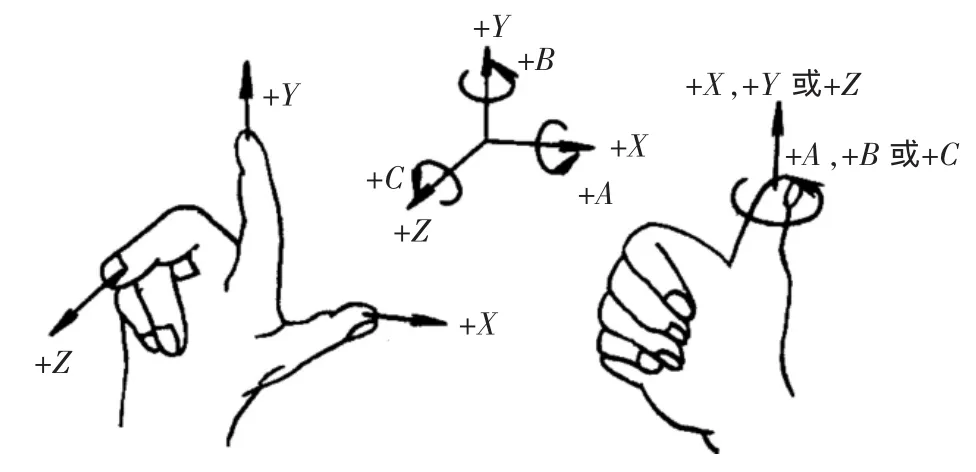
图1 右手直角笛卡尔坐标系

1.1 数控车床坐标轴判别

大多数数控车床具有X和Z两个直角坐标轴，一般平床身是前置刀架，斜床身多为后置刀架，如图2 所示。 图中的｛M1｝、｛W1｝、｛T1｝和｛R1｝分别表示后置刀架数控车床的机床坐标系、工件坐标系、刀具坐标系和机床参考点坐标系， 同理 ｛M2｝、｛W2｝、｛T2｝和｛R2｝是表示前置刀架机床相应坐标系，其中机床坐标系原点是固定的，故该坐标系可作为全局坐标系，其他三个可作为动态坐标系，他们之间可利用坐标变换矩阵求解，理论上卡尔丹角矩阵是单位矩阵，即认为四个坐标系是绝对的相互平行且方向相同，为此，数控机床通常是以参考点坐标系来判别各轴位置与方向(计为“规则2”)。在数控车床中，通过试切对刀等方式来确定刀具坐标系与工件坐标系的位置关系(如重合关系)，即可为数控程序控制刀具相对于工件在工件坐标系中完成准确地加工提供保证。

图2表示车床前置、后置刀架 (以四方刀架为例)的直角坐标轴，其中Z坐标轴是平行于机床主轴，即平行于工件回转轴线的坐标轴。在数控机床中Z坐标轴是作为机床主坐标轴，是与机床上提供切削力的主轴轴线相平行或重合的轴(计为“规则3”)。Z坐标轴是数控机床首先要判别和确定的［2］。X坐标轴是平行于工件装夹表面且与Z轴垂直。结合右手直角笛卡尔坐标系和“规则1”可判别数控车床坐标系，如图2中后置刀架T1和前置刀架T2号刀具远离工件的运动方向正是+X和+Z方向，并可判别相应的+Y。图2中后置刀架是斜床身形式，若刀架倾斜角度为α，则图2所示的后置刀架坐标系为刀架旋转－α角后的图形，与其相对应的其他三个坐标系同理。

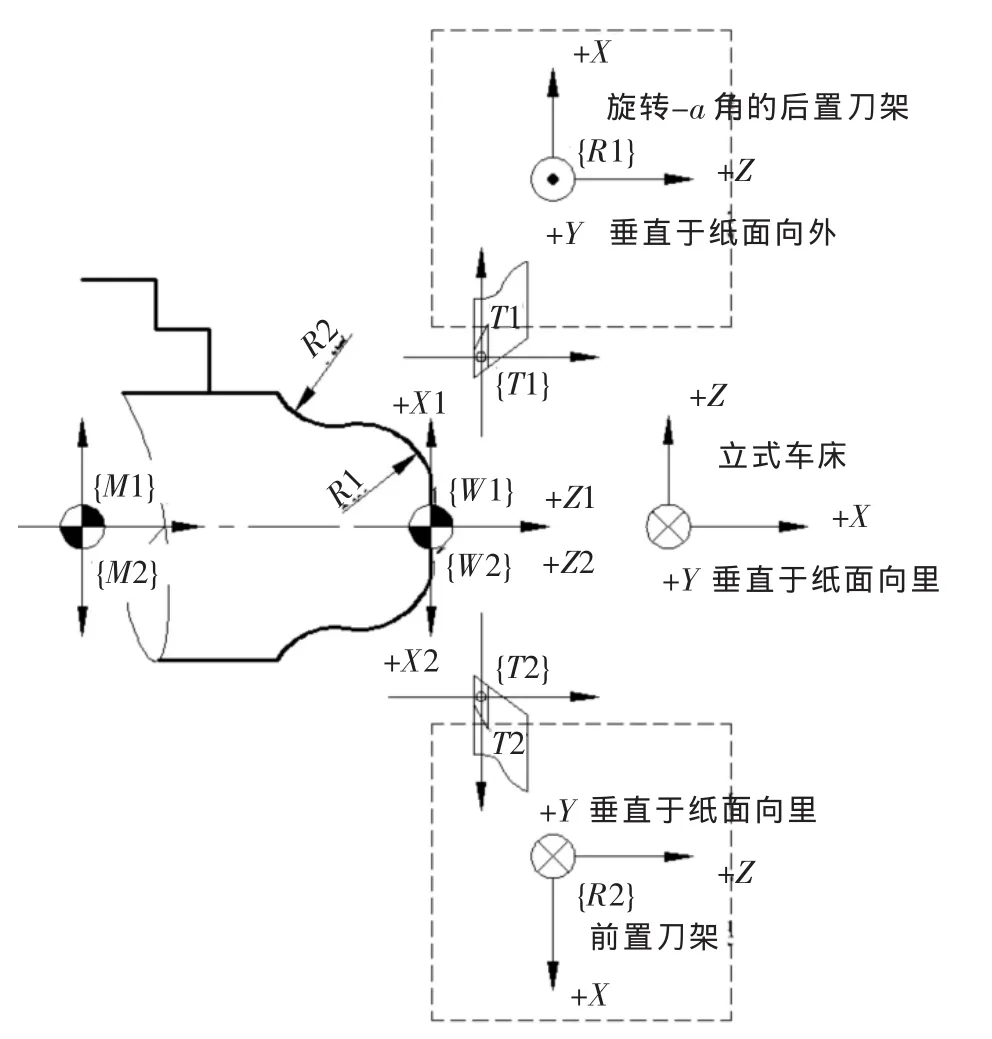
图2 数控车床坐标系

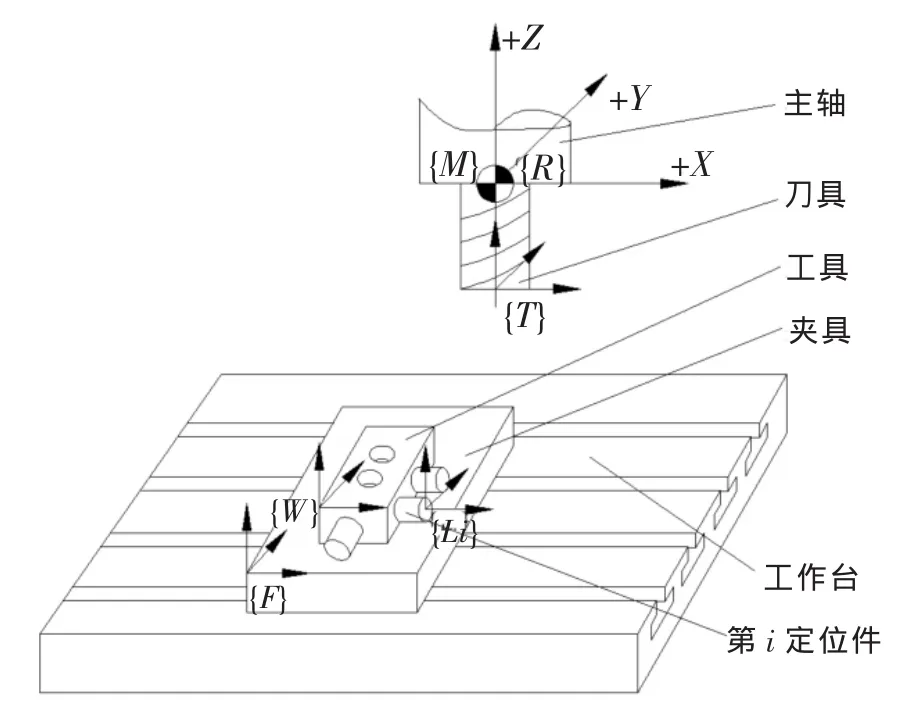
图3 立式数控铣床(加工中心)坐标系

1.2 数控铣床坐标轴判别

通常数控铣床和加工中心机床是由X、Y、Z坐标轴组成，如图 3 所示。图中｛M｝、｛R｝、｛T｝、｛W｝、｛F｝和｛Li｝分别表示机床坐标系、参考点坐标系、刀具坐标系、工件坐标系、夹具坐标系和第i定位件坐标系。这些坐标系也满足绝对的相互平行且方向相同的原则，即同一机床中根据机床坐标系或参考点坐标系所确定的右手笛卡尔坐标系，其他坐标系都满足与之相互平行且方向相同的原则 (计为 “规则4”)。 根据“规则 1、2、3”首先确定+Z。 以平行于工作台最长的尺寸为X坐标轴，平行于工作台最短的尺寸为Y坐标轴(计为“规则5”)。对于立式数控铣床，面对刀具主轴向立柱看时，X坐标轴正向指向右［2］(计为“规则6”)，最后结合图1可判别+Y。立式数控铣床如果在空间上绕Z轴旋转180°后，再绕X轴旋转 90°即为一台卧式数控铣床(计为“规则 7”)。

图4 附加轴与第一轴系的关系

1.3 数控机床附加轴坐标系

任何类型数控机床都可以设置一根或多根附加轴，来满足不同功能需求。通常增加旋转的附加轴A、B、C比较多，如车削中心在刀架上安装动力头，即附加了C轴功能；如立式数控铣床的工作台上安装回转工作台或沿轴方向安装伺服电机控制的分度头(类似于万能分度头装置)，则机床附加了C轴或B轴功能。当然机床也可以附加平行于X、Y、Z的坐标轴系，如图4所示，其中第一行的X、Y、Z坐标轴系称为第一轴系(主坐标系)；第二行为旋转轴系；第三、四行为第二和第三轴系，以此类推，目前SIEMENS840D可控制轴数达30根以上；图4中每列表示该坐标轴都与相应的第一轴有关系［1］，如A绕X的旋转轴，U、P是平行于X的轴等。

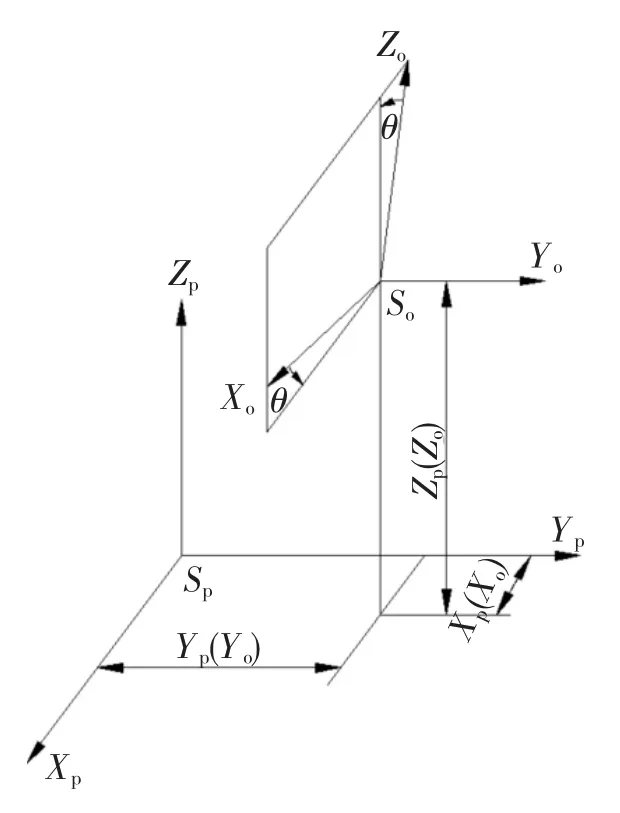
图5 数控机床坐标系变换

1.4 数控机床空间几何关系

研究和分析数控机床空间几何关系对机床精度具有十分重要的作用。分析数控机床运动副之间的误差，都需建立一系列的坐标系，故每个运动副都需建立一个坐标系，在保证实际测量简便性和精确性的基础上，通常在机床的固定部件上建立一个全局坐标系，以确立机床运动副之间的相互关系，但每一个坐标系的建立必须满足“规则1”。为了简单阐述空间几何关系，本节以坐标变换矩阵加以说明，如图5所示。假定机床原坐标系So(Xo，Yo，Zo)和新坐标系Sp(Xp，Yp，Zp)，空间任意点 M 在 So和 Sp坐标系中的位置矢量及其关系分别为：

式（3）中Mop表示从So到Sp的坐标变换矩阵。

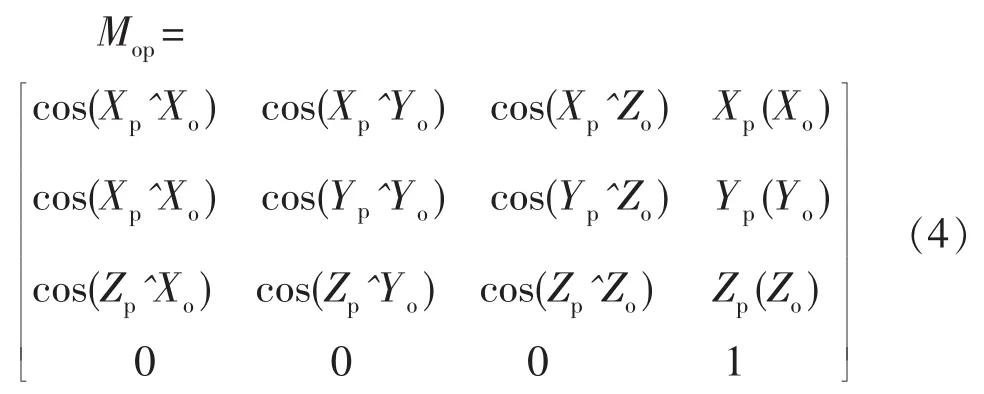
其中Mop的前三行、列表示的是原坐标系So(Xo，Yo，Zo)到新坐标系 Sp(Xp，Yp，Zp)的方向余弦，Mop的最后一列表示 So(Xo，Yo，Zo)的新坐标。

根据式（1）—（4），由于数控机床坐标系统很多，可以利用式（3）原理，仅需遵守矩阵代数的乘法规则，即可得以下方程：

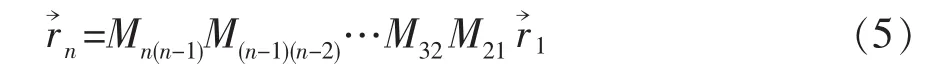
式（5）表示从 S1到 S2，从 S2到 S3，…，从 S(n-1)到 Sn的逐次坐标变换。

式（1）—（5）即表示了数控机床的空间几何坐标关系。

2 数控加工过程中的刀具位置判别

2.1 刀具半径的左、右补偿判别

在数控加工过程中经常使用刀具补偿功能，分别采用G41和G42进行左右补偿，下面以笛卡尔坐标系进行判别。刀具在所加工轮廓的笛卡尔坐标系的某个平面内，沿第三个坐标轴负方向(即从第三个坐标轴的正向向负向观察)，并顺着刀具进给运动方向观察，当刀具处在切削轮廓右侧时，称刀具半径(车床中称刀具刀尖半径补偿)右补偿，当处在切削轮廓的左侧时则为左补偿(计为“规则8”)。如图2所示，车削R1和 R2轮廓时，采用｛W1｝工件坐标系时，根据“规则8”，编程人员是正对着工件观看，T1刀具刀尖半径采用右补偿；若采用｛W2｝工件坐标系时，根据“规则8”，编程人员是反对着工件观看(即从纸面背面观察)，T2刀具刀尖半径也是右补偿，而非左补偿。在数控铣床中建立刀具半径补偿时，如图6（a）和图 6（b）所示，在 G17 和 G18 平面内，由于第三个坐标轴正方向(即+Z和+Y)不同，加工相同轮廓时，刀具的半径左右补偿是不一样的，在实际应用中默认的是图 6（a）。

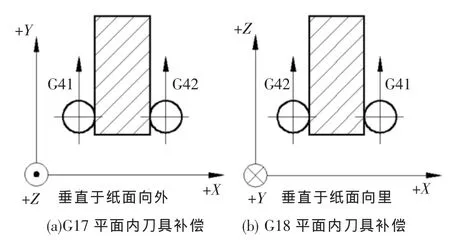
图6 数控铣床的左右刀具半径补偿

2.2 刀具刀尖方位的判别

数控车床中刀具补偿G41/G42是不带参数的，其补偿号由T代码指定，其刀具刀尖半径补偿号和刀具偏置补偿号对应。在刀具补偿寄存器中(图7)分别输入刀尖半径补偿值和刀尖的方位号在同一番号中R列和T列，R列和T列需同时输入相应数值，否则程序调用G41/G42无效。图8所示的是后置刀架的刀具方位，共有10个方位号(即0—9号)，A点表示刀具刀位点，+X和 +Z是机床直角坐标轴正方向。那么图8中0—9号刀位如何判别？根据“规则4”，将+X和 +Z的机床直角坐标轴系平移到各个刀具标有“+”的圆心处构成各个刀具坐标系，结合“规则8”所述的“沿第三个坐标轴负方向”观察，结合直角坐标系中象限的规定。图9表示了刀具刀尖方位A点及其所在象限位置来确定该刀具刀位号0—9，从而得出图8所示的10个方位。为此，图2中T1刀具在｛T1｝坐标系中，刀具刀尖方位号为“3”；图 2中 T2刀具在｛T2｝坐标系中，刀具刀尖方位号也为“3”。

2.3 数控加工的顺逆圆弧判别

圆弧是数控加工中常见的加工对象，数控程序G02/G03分别表示顺圆弧和逆圆弧插补，同理利用笛卡尔坐标系中“规则8”所述的“沿第三个坐标轴负方向观察”，当圆弧所在平面内是顺时针方向则为顺圆弧，否则为逆圆弧。图2中加工R1和R2圆弧的顺逆，在+X1和+Z1构成的｛W1｝工件坐标系中，R1为逆圆弧采用G03指令加工，R2为顺圆弧采用G02指令加工；同理在+X2和+Z2构成的 ｛W2｝工件坐标系中，R1也为逆圆弧采用G03指令加工，R2也为顺圆弧采用G02指令加工。运用“规则8”，可分别判断数控铣床(或加工中心)在G17和G18指定平面内的G02/G03，如图10所示。

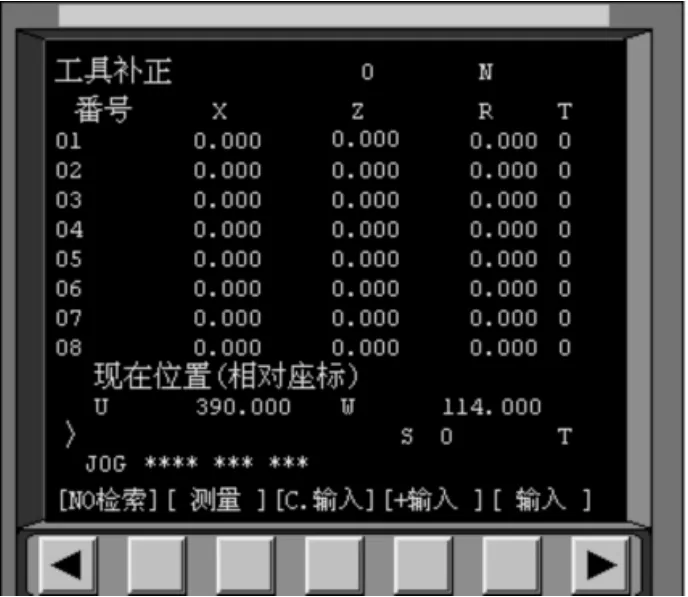
图7 数控车床刀补寄存器界面

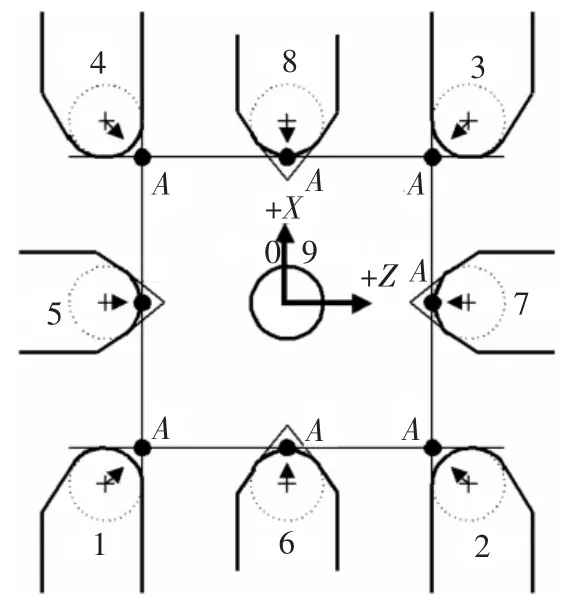
图8 后置刀架数控车床刀尖方位号

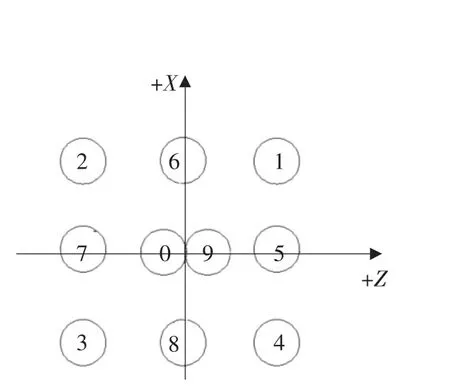
图9 后置刀架数控车床刀尖方位象限点

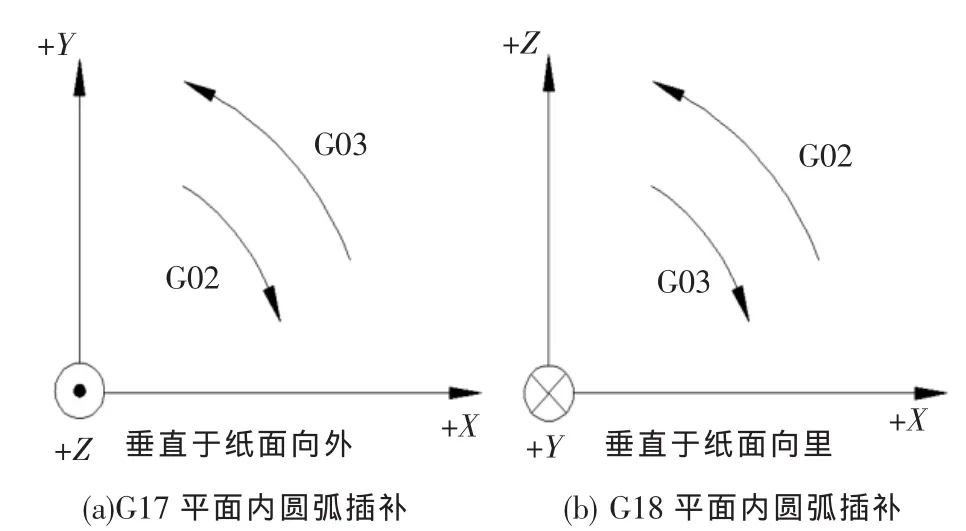
图10 数控铣床的圆弧插补方向

3 应用与误区

3.1 数控机床空间几何误差模型的理论应用与误区

建立数控机床空间几何误差模型必须依赖于右手直角笛卡尔坐标系及其空间坐标变换关系，其建模方法有几何建模法、误差矩阵法、二次关系模型法、机构学建模法及多体系统理论建模法等。目前运用多体系统理论进行误差建模比较流行。文献［3］采用多体系统理论完成了五轴数控机床的综合误差建模，但文献［3］对UCP710机床结构所建立的坐标系不是笛卡尔坐标系，所建立的误差模型可能与实际机床各个坐标轴的误差不符，这会使实际机床坐标轴的精度检测和补偿产生错误。为此，无论采用何种建模方法和技术，一定要以笛卡尔坐标系为准则去建立机床机构上各个坐标系，这是研究人员应当注意的问题。

3.2 刀具位置判别与误区

（1）很多教科书及文献中对刀具半径左右补偿问题的描述缺少了 “刀具在所加工轮廓的笛卡尔坐标系的某个平面内，沿第三个坐标轴负方向(即从第三个坐标轴的正向向负向观察)”这段话，使得“规则8”不完整，致使一些数控人员对并非G17平面(即数控机床上默认的XY平面)时，也按照缺少前段语句描述的“规则8”去判断，这是实际应用的误区。

（2）在判别顺逆圆弧时，由于G17平面判断较多，数控人员同样对“规则8”所述的“沿第三个坐标轴负方向观察”忽略，这是实际应用中常见误区。在数控车床中，一些实践人员甚至教师在讲解顺逆圆弧时，总结出以后置刀架来判别工件轮廓的圆弧方向，通过笛卡尔坐标系判断图2可知，这种经验的确十分有效，但作为一名真正数控加工人员一定要知其所以然，否则在复杂的车铣复合加工中心上判别刀具位置就困难了。

（3）文中介绍了后置刀架数控车床刀尖方位的判别方法，可见刀尖方位不是死记硬背，而是根据笛卡尔坐标系进行判别，具有规律性，这是很多数控人员容易忽视的问题。

4 结 论

数控机床是以右手直角笛卡尔坐标系为其标准坐标系，根据机床结构、运动机构及其加工运动过程的空间关系，可以建立更多个笛卡尔坐标系。文中总结了8个主要规则，并举例分析了笛卡尔坐标系在机床空间几何关系和刀具位置判别等方面的应用及常见误区，为数控工程人员、科研及教学人员提供指导。

[1]Peter Smid.数控编程手册[M].罗学科,译.北京:化学工业出版社，2006.

[2]顾晔,楼章华.数控加工编程与操作[M].北京:人民邮电出版社，2009.

[3]王秀山,杨建国,闫嘉钰.基于多体系统理论的五轴机床综合误差建模技术[J].上海交通大学学报，2008，42(5):761-764,769.

Research on Application of NC Machine Tools of Descartes Coordinate System

ZHANG GuozhengYANG Haihui
(Anhui Technical College of Mechanical&Electrical Engineering，Wuhu 241000)

One's right hand and angle descartes coordinate system is the standard coordinate system of NC machine tools.It can judge the relationship of geometrical space of machine tools,and also judges the compensation of tool's radius,nose of tool and the way of clockwise-arc or counterclockwise-arc during machining process.The practical rules are summarized that for showing the practical application of descarres coodinate system,and some errors of NC machining engineer are proposed.

descartes coordinate system；NC machine tools；coodinate axis judging；tool position

TG659

A

1673-1980（2012）01-0121-05

2011-10-24

安徽高等学校省级自然科学研究项目（KJ2011B037）

张国政(1980-)，男，博士，讲师，研究方向为数控加工技术及应用、CAFD技术、齿轮数控加工技术。