基于Simulink的双电磁振动台并机控制方法研究

姜夏 郭军 丁佐琳

（航天四院四零一所，西安 710025）

基于Simulink的双电磁振动台并机控制方法研究

姜夏 郭军 丁佐琳

（航天四院四零一所，西安 710025）

基于现有双振动台同步驱动控制技术，运用simulink进行系统仿真。通过调节两振动台间的功率驱动信号的大小，可缩小两台间响应的差值，完成振动系统的响应同步控制。

双电磁振动台；PID；系统仿真；同步控制

电磁振动台配以振动控制系统可以完成航天器的振动环境模拟试验，对于质量大的试验件或对试验件施加更大的加速度时,两台电磁振动台并联才能达到试验要求。

1 现有同步控制方法及其存在的问题

现有双振动台正弦振动试验采用振动和相位控制器分别对双振动台的振幅和相位进行控制的方法，其原理如图1所示。外闭环主要控制振动台的幅值，由振动控制器根据响应信号得到的响应谱与参考谱进行比较，计算出误差谱，并不断修改驱动谱，使振动控制点的响应与参考值在允许误差范围内。内闭环主要修正两路驱动信号的相位，霍尔传感器通过实时监测振动台动框电流并提供与功放输出电流成正比的电压信号，电压信号反馈给相位控制器，控制器根据两路信号的相位差来调节驱动信号，实现双振动台的同步驱动控制。

图1 双振动台振幅与相位双闭环控制原理图

上述双振动台控制系统是对于同步驱动信号的控制，认为两振动台本身无差异，在忽略振动台本身制造工艺的差异下对驱动信号进行控制，使功率放大器输出的信号一致。实际上在进行大吨位振动试验时，两振动台的制作工艺或环境变化可能引起磁路系统的差异，导致两台在磁轭与磁极之间产生的均匀恒定的工作气隙磁场不同。而对两振动台给定相同驱动信号时，其响应信号的幅值及相位都有差异，致使无法实行双台机的同步响应振动。

2 双振动台响应的同步控制方法

2.1 响应同步控制原理

考虑两振动台自身差异可能对同步响应信号造成的影响，对两振动台的振动响应信号及两功率放大器输出信号进行实时检测。计算振动台响应信号的差，实时调节其中一路信号源，调节后两功放的输出信号可能为异步信号，但最终实现对两台振动台的同步响应控制，使两者振动信号达到精准一致，其控制原理图如图2所示。

图2 双路实时闭环反馈控制原理图

2.2 单电磁振动台PID控制

由于大型航天器振动试验一般运行在低频下，此时台面与动圈骨架间完全刚性，则振动台运动部件简化为单自由度系统，如图3所示。

图3 振动台低频简化力学模型

图中m2为振动台面质量，C2为可动系统相对于外壳的阻尼，k2为可动系统相对于外壳的刚度。当动圈中通入正选激励电流频率为ω时，振动台受到的推力为：

式中:B为工作气隙中磁感应强度；i为动圈中通过的电流；l为动圈导线的长度；I为电流幅值。根据振动理论，可以得到运动部件的振动力学方程：

式中：m为运动部件和负载总质量；F(t)为振动台动圈所受推力。图2中功率放大器是一个理想的电流反馈功率放大器，其输出阻抗无穷大，对于动圈而言，相当于一个恒流源，其电学方程式为：

其中：Re为电流功放中反馈电阻；ka为功放电压放大倍数；U为信号源输出电压。

对式（2）、（3）进行拉普拉斯变换，初始条件为

则，恒流位移传递函数为：

由公式（4）可得到电磁振动台在低频恒流激振下的位移传递函数，在仿真系统中加入白噪声假设为周遭环境对电磁振动台的影响，并利用PID对系统进行修正，其原理如图4所示。图4中最优化模块实现simulink中PID参数最优化计算。由于制造工艺引起两振动台在同一激励下产生不同的磁场，则振动台二阶系统中的kg将不同，对振动台进行系统仿真，经过PID修正后得到的PID参数见表1，其中p表示加入白噪声的能量。

图4 单台电磁振动台PID控制原理图

表1 电磁振动台参数设定及PID参数

修正前后两振动台的系统阶跃响应如图5所示，其中实线为原系统的阶跃响应，虚线为加入PID修正后系统的阶跃响应。由图5可见系统的稳定性在PID修正后得以提高。

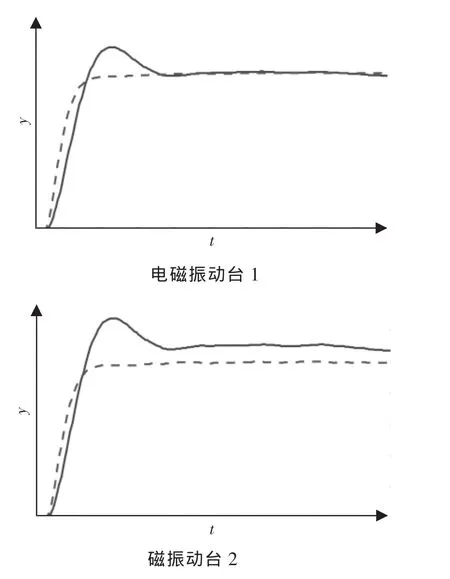
图5 电磁振动台系统阶跃响应与PID修正后的阶跃响应

2.3 双振动台响应同步的控制方法模拟

双电磁振动台并机后，在给定相同正弦信号驱动下，根据表1中两者之间存在的差异，检测两振动台响应信号的差值，以电磁振动台1为基准，对电磁振动台2的正选驱动信号进行补偿，从而使两振动台响应之间的差值逐步缩小，系统原理如图6所示。

图6 双振动台响应同步控制原理图

图7 双振动台正弦激励响应

对双振动台进行仿真后正弦激励响应如图7所示。左图中两振动台由于自身差异造成在相同驱动下响应不同步的情况，点线即为响应差值。右图为加入增益控制后，两台响应之间的差异。从仿真可知，增益选取越大，响应信号差越小，选取增益值至10时，振动台几乎同步。

3 结 论

本文通过模拟双电磁振动台同步驱动下的系统，获得两者之间由于自身差异所造成的响应不同步现象。同时通过调节两台间的驱动信号，缩小响应差值，完成振动系统的响应同步控制，从而严格保证双振动台同步运行。本文可为大型航天器的环境振动试验所用并机系统控制提供新思路。

[1]高非.数字式电流相位同步控制器的研究[D].北京：国防科技大学，2005：2-4.

[2]李红强.电动振动台动圈的有限元分析与优化设计[D].苏州：苏州大学，2006：6-12.

[3]潘良明.振动校准装置测控系统的开发与研究[D].杭州：浙江大学，2006：13-18.

[4]邱汉平，冯咬齐.双振动台正弦振动同步控制新方法研究[J].航天器环境工程，2006(6):1-2.

[5]侯瑞，陈国平.振动台虚拟试验的建模和仿真研究[J].力学季刊,2008(2):1-2.

[6]孙明.科研教育用振动台系统若干关键技术研究[D].杭州：浙江大学,2008：7-15.

Abstract：Based on the existing synchronous control technology of dual-shaker,simulink is used in system simulation of dual-shaker.The results show that the difference of the response between dual-shaker is narrowed to control the synchronous response of the vibration system by adjusting the power drive signal of dual-shaker.

Key words：dual-shaker;PID;system simulation;synchronous control

Simulink-based Control Method for Dual-Shaker

JIANG Xia GUO Jun DING Zuolin
(401 Institute of No.4 Aerospace Institute,Xi′an 710025)

TP274

A

1673-1980（2012）02-0153-03

2011-10-13

姜夏（1986-），女，航天四院四零一所在读硕士研究生，研究方向为测试计量技术及仪器。