空气在三角形波纹通道内湍流流动与换热的数值研究

阴继翔，杨 刚

（太原理工大学 电气与动力工程学院，太原 030024)

换热器的强化一直是传热领域倍受重视的研究课题，高效紧凑换热器广泛的工业需求促使设计人员不断研发新的强化换热表面。一次表面换热器是一种新型高效、轻质结构的热交换器，其中三角形波纹板换热器因其制造工艺简单、综合性能良好而被广泛应用。

曾有许多学者对三角形波纹通道内的流动与换热进行过实验与数值研究。文献［1］使用萘升华质、热比拟技术，研究了三角形波纹通道表面的局部及平均换热系数，实验发现在层流区段，其换热系数的提高不太明显，当流动进入非稳定的湍流区时，其换热系数是平直通道的3倍。Reinhard Wurfel［2］等人对人字型波纹板换热器的传热与压降进行了实验研究，发现波纹板的倾角是影响换热器性能的主要因素。文献［3］对空气在不同高度波纹流道内的流阻与传热过程的模拟计算表明，波纹高度是影响流动阻力与传热过程的重要因素。Wirtz和Greiner［4-5］对单侧和双侧三角形波纹板通道的内流动与换热特性的研究发现，与具有最小板间距的平行板通道相比，三角形波纹板通道的换热和阻力均有所增加。E.A.M［6］等人实验研究了不同相位差及不同板间距的三角形波纹板通道内压降和换热系数随Re变化的规律，结果表明，波纹板间距和上下板的相位差有不同程度的影响，通过对不同结构波纹板性能因子j／f的比较，给出了最优的波纹板结构。前人的研究，主要集中于层流流动与换热的范围，有关流动在较高Re区的过渡流及换热特征的数值研究涉及较少。为此，笔者运用Fluent商用软件对三角形波纹通道内过渡区的流动与换热特征进行数值模拟，考察三角形形状参数及Re对流动阻力、换热系数及综合性能的影响，并寻求使得通道性能最佳时的形状参数，旨在为三角形波纹通道换热面的设计及选型提供参考依据。

1 物理问题及数值方法

1.1 物理问题及控制方程

图1为一个周期的三角形波纹通道的示意图。流体流经周期性变化的通道时，当主流方向的波纹周期数目超过4～6后，流动与换热便进入周期性充分发展段［7］，故可以采用一个周期的单元通道作为计算区域。

图1 三角形通道一个周期示意图

本研究的周期性波纹通道的壁面形状函数为：

其中，K、S是形状参数，K决定了波纹板的倾角，S决定上下板间的距离。该通道的波纹振幅为A，通道周期长度为L，定义间距比为ε＝S／L（0.125，0.25.0.375，0.5)，波纹纵横比为γ＝2A／L（0.125，0.25，0.375，0.5)。计算采用物性参数为常数的空气，并假设流动为二维准稳态湍流流动，壁面温度均匀恒定，进出口采用周期性边界条件，其通用控制方程为：

式中：φ＝1；u，v，k，ε分别代表连续方程，动量方程以及k-ε湍流双方程模型；扩散系数Γ和源项Sφ随变量φ不同而具有不同的物理含义。

1.2 计算所用参数的定义

1)雷诺数

式中：uav为流体的平均速度；De为通道的当量直径；ν为流体的运动黏度。

2)平均速度

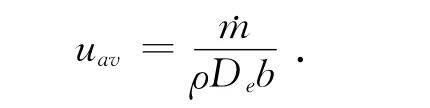
3)达西摩擦阻力系数

β为通道一个周期的压力梯度。

4)平均努塞尔数

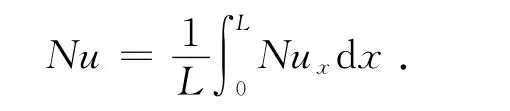
5)传热因子

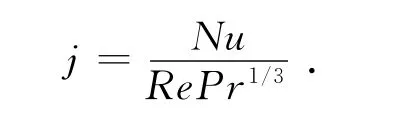
其中，Pr为普朗特数。

1.3 算法及网格的生成

采用商用Fluent软件对通道内的流场及温度场进行数值模拟，压力与速度的耦合采用SIMPLEC算法完成，方程的离散采用二阶迎风格式，湍流计算采用k-ε双方程模型。由Gambit软件生成非结构网格，为有效求解近壁处较大的速度和温度梯度，在进出口处壁面附近布置相对较密的网格节点。所有模拟计算的收敛残差为：连续性方程、动量方程、湍动能方程及湍流耗散率方程均为10-5，能量方程为10-6。

2 算法考核

当波纹高度A为零时，波纹通道即为平直通道。将本文的算法应用于平直通道的计算，Nu及f的数值结果分别与由实验关联式Dittus-Boelter公式（3)和Filonenko公式（4)计算所得的Nu及f对比见图2所示。数值解与实验关联式计算结果吻合较好，验证了本文算法的有效性。

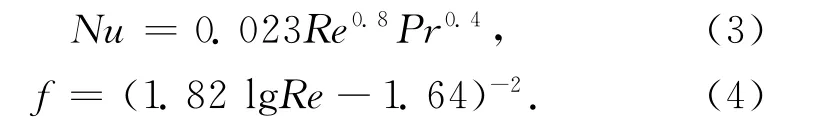
图2 Nu及f的模拟结果与解析结果对比

3 结果分析与讨论

3.1 流动特性分析

流函数随着Re数、间距比ε以及波纹纵横比γ的变化如图3所示。γ为0.125时，随着Re的增加，通道内流线几乎保持互相平行，流动没有出现漩涡，只是在壁面附近有流动分离现象发生。这是由于波纹振幅较低时，黏性力占主导作用，惯性力的作用相对较小。随着γ的增加，通道入口处上壁面的附近、波谷处以及下壁面波峰处均出现漩涡，其中上壁面入口处的漩涡随着Re及γ的增加而不断增大，随着惯性作用的增强，漩涡的中心沿着流动方向逐渐向下移动。

图4显示了流场随着间距比ε及雷诺数Re的变化关系。由图可见，在Re相同的条件下，随着ε的增加，通道上壁面的漩涡沿着流动方向不断增大，增加了动量输送，促进了流体间的混合，并最终几乎占据了整个上半壁面。当ε保持不变时，随着Re的增加，惯性作用增强，漩涡强度增强，同时漩涡的中心向通道中心区域靠近。

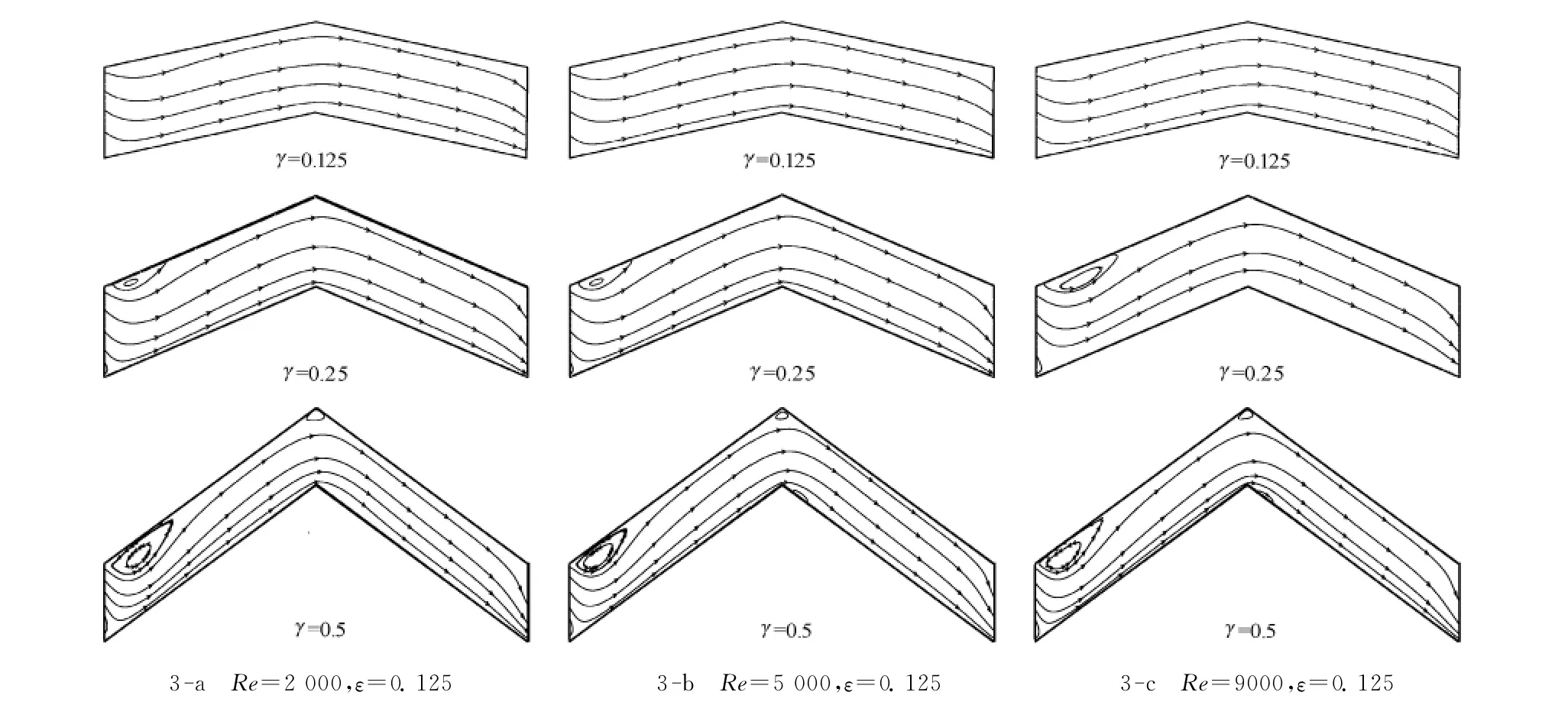
图3 不同雷诺数Re和几何因子下的流场分布

图4 不同雷诺数Re和间距比ε对流场影响

3.2 通道流动阻力特点分析

阻力系数f随雷诺数Re、间距比ε、波纹纵横比γ的变化如图5所示。首先，随着Re的增加，所研究通道的f降低，并且在Re＝5000以后，f的变化趋于平缓。在图5-a中，当Re＜5000，随着ε的增加，阻力系数f先增加，后又降低；当Re＞5000时，阻力系数的值随着ε的增加而增加，这些变化关系与图4的流动特征相对应。从图5-b可以看出，阻力系数f随着γ的增加而增加。

由计算结果拟合得到如下的关系式：

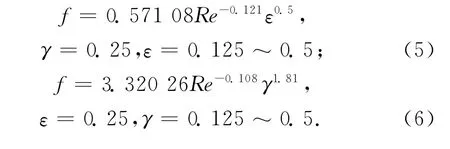
3.3 换热特性分析

表面平均努谢尔特数Nu的变化规律见图6所示。由图6-a可见，随着ε的增加，Nu数先增加后减小，即波纹板间距增加到一定程度，换热开始下降，因而存在一个使得换热达到最高的最佳ε值。由图6-b可见，随着γ的增加，换热不断增大，这是由于随着波纹板振幅的增加，通道的换热表面积增加，同时流体在通道中的停留时间增加所致。由计算结果拟合得到如下的关系式

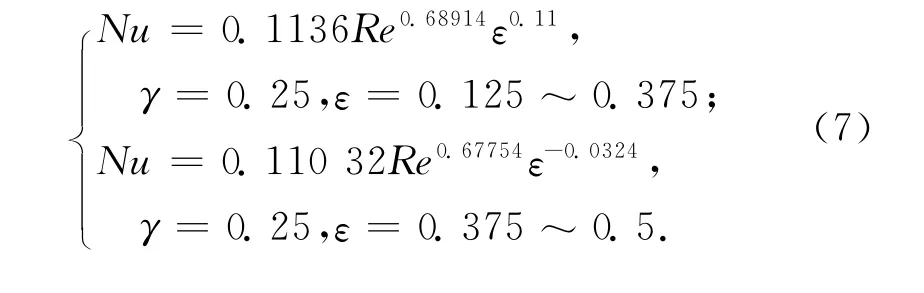
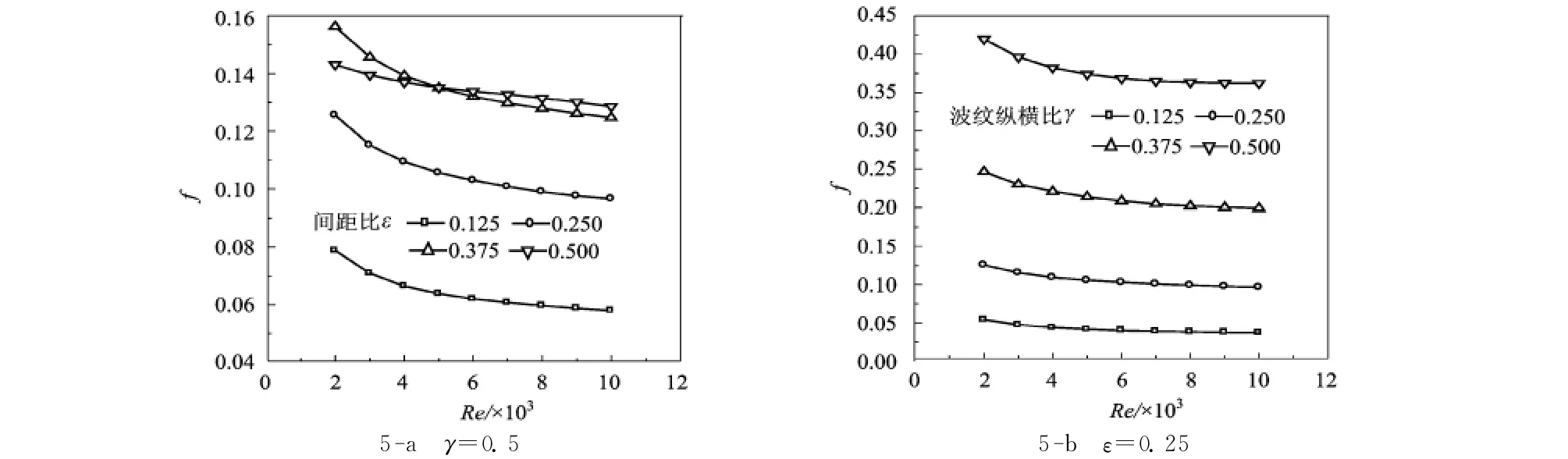
图5 Re、ε及γ的变化对阻力系数f的影响

图6 Re、ε及γ的变化对平均努塞尔数Nu的影响

3.4 综合性能参数分析

换热器设计的原则就是在较低压损下获得较高的换热量，因而需要对流动与换热进行综合性能分析。笔者选用参数j／f作为综合性能的评价指标。图7给出了综合性能参数j／f随Re的变化关系。其值越大，即在图中的位置越高，表示通道所需的流通面积越小。由图可见，波纹通道间距的减小或者是波纹振幅的降低，均能够获得较高的性能因子j／f。当波纹纵横比（γ)一定时，随着波纹板间距的增加，性能因子在雷诺数Re＜4000时，先减少，之后又增加；Re＞4000时，j／f随着波纹间距的增加而降低。当波纹板间距比（ε)一定时，随着波纹板振幅的增加，性能因子不断降低。从图中不难看出，两种情况下均在较小Re时能够获得较高的换热量，而且波纹板间距的减小或者波纹板振幅的降低均能得到较高的换热性能。

图7 Re、ε及γ的变化对综合性能参数j／f的影响

4 结论

通过对波纹板几何因子及不同质量流量对流动与换热性能影响进行分析，得出如下结论：

1)在雷诺数Re相同的情况下，Nu数随着间距比ε的增加先增加后减少，因而在波纹振幅一定时，存在一个最佳的波纹间距ε值，使得换热最高；而Nu数随波纹纵横比γ的增加而增加，即在波纹间距一定时，换热随着波纹振幅的增加而不断提高。

2)不同结构通道的流动阻力系数f随Re的增加而减小，在Re增长到一定值时，f的变化变得缓慢.当γ＝0.25，Re＜5000时，随着ε的增加，f先增加后又降低；当Re＞5000时，f随着ε的增加而增加。

3)波纹纵横比γ对换热及流动的影响均大于间距比ε对换热及流动的影响。

4)通过对比分析几何因子及不同雷诺数下的性能因子j／f表明，小间距或低振幅的波纹板有利于换热性能的增强。

［1］Goldstein J L，Sparrow E M.Heat transfer characteristics for flow in a corrugated wall channel［J］.ASME J Heat Transfer，1977，99（2)：187-195.

［2］Reinhard Wurfel.Experimental investigation of heat transfer and pressure drop during the condensation process within plate heat exchangers of the herringbone type［J］.Int J Thermal Sciences，2004，43（1)：59-86.

［3］吴新华，孙刚，匪趸困.空气在不同高度波纹流道内的流阻与传热的数值分析［J］.哈尔滨工程大学学报，2007，28（10)：1100-1103.

［4］Wirtz R A，Huang F，Greiner M.Correlation of fully developed heat transfer and pressure drop in a symmetrically grooved channel［J］.ASME Journal of Heat Transfer，1999，121（1)：236-239.

［5］Greiner M，Chen R F，Wirtz R A.Enhanced heat transfer pressure drop measure from a flat surface in a grooved channel［J］.ASME Journal of Heat Transfer，1991，113（2)：498-500.

［6］Elshafei E A M，Award M M.Heat transfer and pressure drop in corrugated channels［J］.Energy，2010，35（1)：101-110.

［7］Ciofalo M，Stasiek J，Collins M W.Investigation of flow and heat transfer in corrugated passages：numerical simulations［J］.Int J Heat Mass Transfer，1996，39（1)：165-192.

［8］杨世铭，陶文铨.传热学［M］.北京：高等教育出版社，2006：246-248.