一类具有可修复储备部件的人－机系统解的指数稳定性

姜英秀， 韩筱爽

（1．延边大学教务处，吉林 延吉133002；2．延边大学科学技术学院，吉林 延吉133002）

一类具有可修复储备部件的人－机系统解的指数稳定性

姜英秀1， 韩筱爽2

（1．延边大学教务处，吉林 延吉133002；2．延边大学科学技术学院，吉林 延吉133002）

针对具有2个运行部件和1个储备部件，故障修复时间服从一般分布的人－机系统模型，运用泛函分析的方法和Banach空间上的线性算子半群理论，证明了严格占优本征值的存在性，并通过分析系统本质谱界经过扰动后的变化，证明了在一定条件下系统的动态解以指数形式收敛于系统的稳态解．

严格占优本征值；本质谱界；指数稳定性

0 引言

文献［1］中研究了具有2个运行部件和1个储备部件，系统故障修复时间服从一般分布的人－机系统模型的可靠性，运用线性常微分方程得到了系统在定常状态和非定常状态下故障修复时间、平均故障时间等的一般表达式，并作图分析证实了人为故障对其产生的影响．该系统为并联冗余系统，其中2个部件并联工作，1个冗余部件处于储备状态，任何时刻只要有1个部件正常工作均能使系统正常运行，工作部件中任何1个发生故障，储备部件立即补充进入工作状态，并且部件间的替换过程是自动且瞬时完成的．若系统出现部件故障则修复程序立即启动，若所有部件均发生故障则整个系统故障．系统的工作流程如图1所示．i＝0表示2个运行部件和1个储备部件均处于完好状态；i＝1表示1个运行部件因硬件错误而故障，1个储备部件立即补充运行；i＝2表示系统仅有1个部件正常运行而无储备部件；i＝3表示系统由于硬件错误而处于故障状态；i＝4表示系统由于通常错误而处于故障状态；i＝5表示系统由于临界人为错误而处于故障状态．

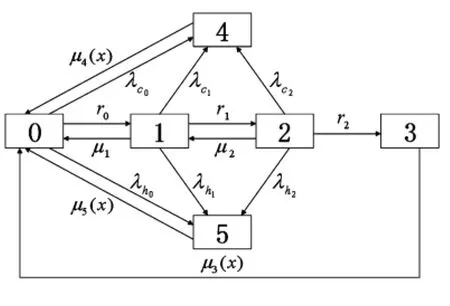
图1 系统的工作流程

上述的模型可由以下积分 －微分方程描述：

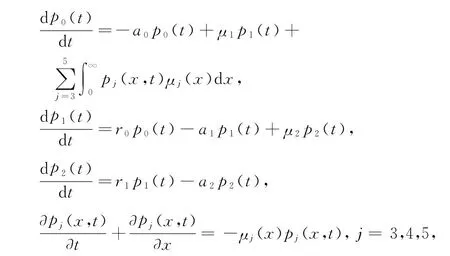
文献［2］运用初等阶梯函数对系统模型中的修复率进行逼近，给出了系统的半离散化模型．这里假

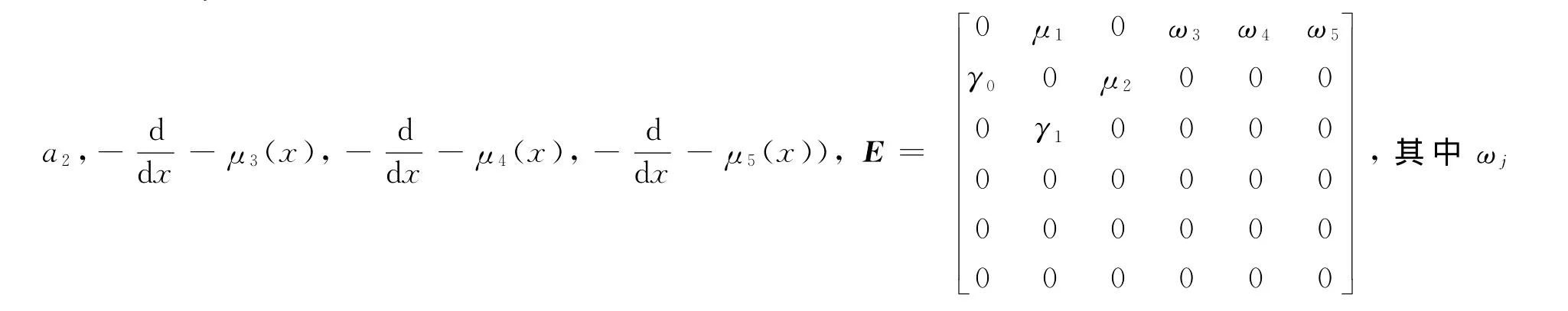
本文基于上述假定，讨论系统的指数稳定性．在文献［2］中取状态空间是1个Banach空间．在X上定义算子A＝diag（－a0，－a1，－取A的定义域为则系统的积分 －微分方程组可描述为Banach空间中的1个抽象Cauchy问题中p（t）＝（p0（t），p1（t），p2（t），p3（x，t），p4（x，t），p5（x，t））．

1 系统的稳态解

文献［3］为研究算子A＋E的预解式R（γ，A＋E）而考虑了预解方程［γI－（A＋E）］p＝y，本文先研究［γI－（A＋E）］p＝0非零解的存在问题．

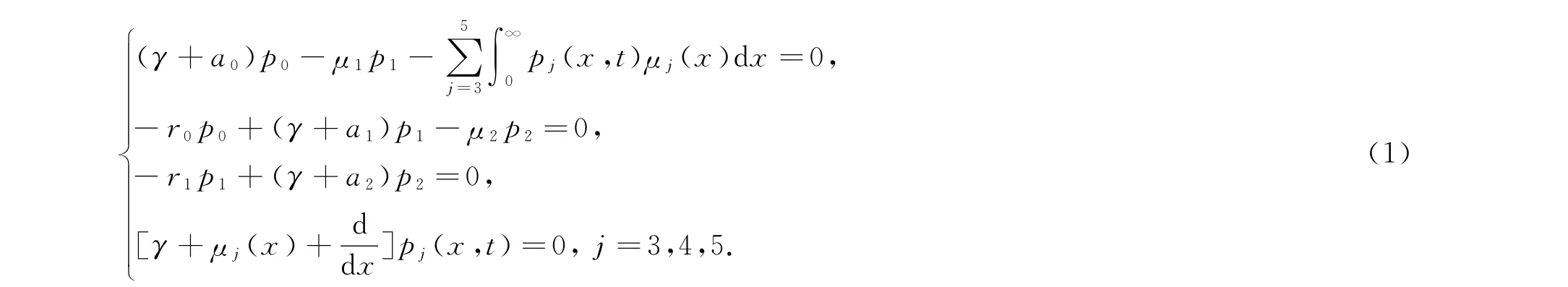
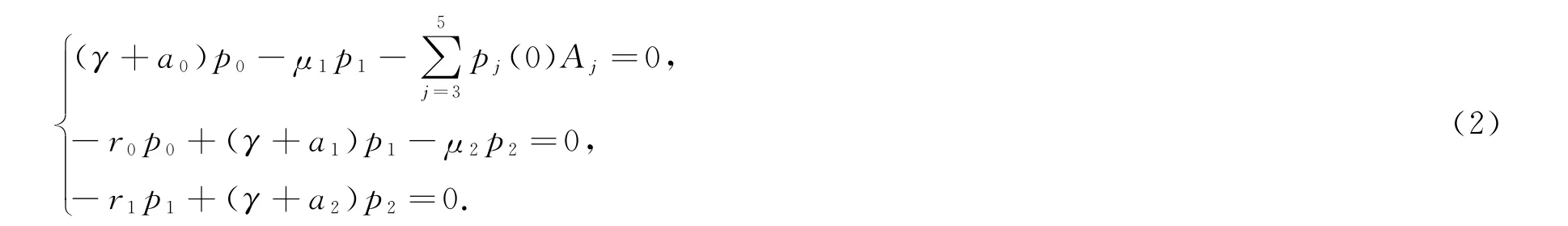
2 系统解的指数稳定性

文献［2］利用c0半群理论证明了算子A＋E可以生成c0半群，并且得到：

引理1［2］①γ＝0是算子A＋E的简单本征值；在X中稠密；④T（t）为压缩c0半群．其中正数

又由于E是1个有限秩算子，因而是紧算子．利用算子半群的扰动定理及半群的紧扰动得定理1：

证明 ① 当Reγ＋c＞0，由定理1知，γ∈ρ（A），则［γI－（A＋E）］＝（γ－A）（I－R（γ，A）E），而A是有限秩算子，因此R（γ，A）A是紧算子．由于紧算子若存在非零的谱值，则必为本征值，因此γ∈ρ（A＋A）的充分必要条件是1不是R（γ，A）A的本征值，因此Reγ＋c＞0时γ∈σ（A＋E）⇔D（γ）＝0．

②易知D（γ）在Reγ＋c＞0上是解析函数，至多有有限个零点，且在有限区域内没有聚点．文献［3］已证明算子A＋E的谱在复平面的左半平面上，虚轴上的点除0点外都在预解集中．又由于0是A＋E的具有正本征向量的简单本征值，再由严格占优本征值定义知0是严格占优本征值．设γ0＝0对任意的其中γk按照实部递减排序，即Reγk＋1≤Reγk，k＝1，2，…，N，因此γ0＝0是A＋E的严格占优本征值．

③根据半群的扰动定理，紧扰动不改变半群的本质谱界．由此知算子A＋E生成的半群T（t）与算子A生成的半群S（t）有相同的本质谱界，故T（t）的本质谱界ω（A＋B）≤ω0（A＋B）．又设＾p0如前，Reγ1＜－ω ＜γ0，根据算子半群的有限展开定理有：对任意的p∈X，θ＝（1，1，1，1，1，1），存在常数M（ω）＞0，使得

上述结果表明，在一定条件下系统的动态解以指数形式收敛于系统的稳态解．

［1］ Yang Nianfu，Dhillon B S．Availbility analysis of a repairable standby human－machine system［J］．Microelectron Reliab，1995，35（11）：1401－1413．

［2］ 方明，韩筱爽．一类具有可修复储备部件的人－机系统解的半离散化［J］．数学的实践与认识，2005，35（12）：142－150．

［3］ 方明，韩筱爽．一类具有可修复储备部件的人－机系统的解的谱特性［J］．延边大学学报：自然科学版，2009，35（4）：305－308．

［4］ Pazy A．Semigroups of linear operators and applications to partial differ［M］．New York：Spring Verlag Berlin Heidelbery，1980：84－102．

The exponential stability of a human－machine system with general failed system repair time distribution

JIANG Ying－xiu1， HAN Xiao－shuang2
（1．The Dean’s Office of Yanbian University，Yanji 133002，China；2．Institute of Science and Technology，Yanbian University，Yanji 133002，China）

We attempt to study a model of human－machine system with general failed system repair time distribution which have two units active and one unit on standby by using the theory of the functional analysis method，especially the theory semi－groups of linear operators on Banach space．Firstly，the existence of the strictly dominance eigenvalue is proved．Then by analyzing the change of the system essential spectral bound under the perturbation，we prove that the dynamic solution is exponential tends to the steady solution of the system．

strictly dominance；essential spectral bound；exponential stability

O177．2

A

1004－4353（2012）02－0108－04

2012－03－22

姜英秀（1978—），男，讲师，研究方向为概率统计．