双电机可拓模糊PID同步控制策略的研究
2012-10-24于彪,朱翚
于 彪, 朱 翚
(苏州大学 机电工程学院,江苏苏州215021)
可拓控制是以20世纪80年代提出的物元分析与可拓集合理论为数学基础[1]。可拓学以矛盾问题为研究对象,以矛盾问题的智能化处理为主要研究内容,以可拓方法论为主要研究方法。可拓控制是基于可拓学来处理控制中的矛盾问题,与传统控制比最大的区别在于:传统控制方法解决的是系统的控制品质问题,可拓控制解决的是系统的控制论域问题。从信息转化的观点来处理控制问题,使被控量从不合格范围转化到合格范围,使控制效果从不满意转化到满意[2]。
然而可拓控制虽善于处理非渐变和质变的问题,对于渐变和量变的问题却存在着局限性。针对这一现实,诸多学者做了大量的研究力图解决此问题。文献[3]利用自适应控制的设计策略来修正可拓控制器的增益参数;文献[4]则认为基于可拓集合的控制策略可以视为广义自适应控制的一种情况。
本文从可拓变换的角度对该问题进行了分析和研究,对经典域进行可拓扩大变换,继而将模糊自适应PID控制策略这种较为成熟的自适应策略引入到经典域中。并以双电机同步传动的控制为对象进行了仿真研究,结果表明可拓模糊PID控制策略具有良好的互补性,综合了二者的优势,能够取得理想的控制品质。
1 可拓模糊PID控制器的设计
可拓模糊(Proportion Integration Differentiation,PID)控制器与基本可拓控制器的结构类似,大致分为特征量抽取、特征模式识别、关联度计算、测度模式识别、控制器输出等5部分,具体结构见图1,其中特征量抽取环节为了理论研究的简便,抽取误差e和误差的变化率e·作为描述系统状态的典型变量,即特征量。特征模式识别环节详细内容参见文献[5-6]。特征量的抽取和特征模式的识别能够定性确定系统运动状态,对于不同的特征模式,特征量对描述系统状态的权重不同,因而在关联度的计算时会有相应的加权系数。

图1 可拓控制器基本结构
1.1 关联函数与测度模式
1.1.1 经典域及可拓域的建立及变换
建立关联函数,首先需要建立特征状态的可拓集合,即确定经典域和可拓域。目前,学者们常用的一种方法是:以被控对象的偏差和偏差微分的容许范围作为经典域,而系统可调的最大偏差和微分偏差作为可拓域。这种划分方式所体现的矛盾双方为是否满足控制指标,这种方式下的经典域用物元模型可以表示为
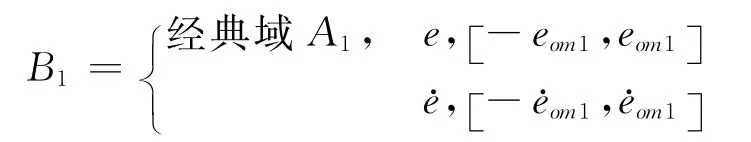
其中,A表示经典域,B表示可拓域表示特征量的经典域分别表示控制指标所要求的系统误差和误差变化率的范围;可拓域用物元模型可表示为

[-em,em]与 []分别表示系统最大可调范围和维持有效控制的最大误差变化率。另外非域可表示为

这种可拓集合建立之后,系统的控制便完全由基于可拓控制算法的控制器来实现,通过关联度的变化从而完成矛盾的转换。然而在控制系统中,为了适应被控对象的时变性,可采用模糊PID等具有自适应功能的控制策略,单纯的可拓控制器难以取得良好的控制效果。为解决这一控制中的矛盾,可对经典域采用可拓扩大变化

[-]与 [-]分别表示模糊PID控制策略可发挥优良控制效果的系统误差及误差变化率范围,相应的可拓域应为
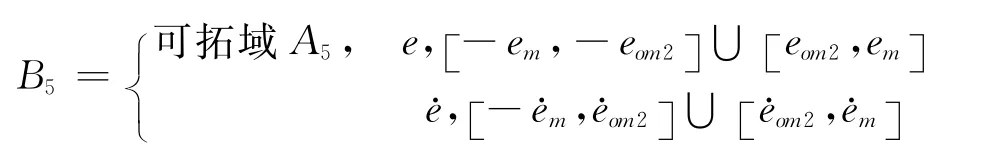
这种可拓集合的建立方式体现的矛盾双方是能否用模糊PID控制策略可以取得良好控制效果。
描述系统特征状态的特征模式及可拓集合见图2。
1.1.2 关联度计算
设e-特征平面的原点为S0(0,0),定义平面上的任意一点S(e)满足关联函数

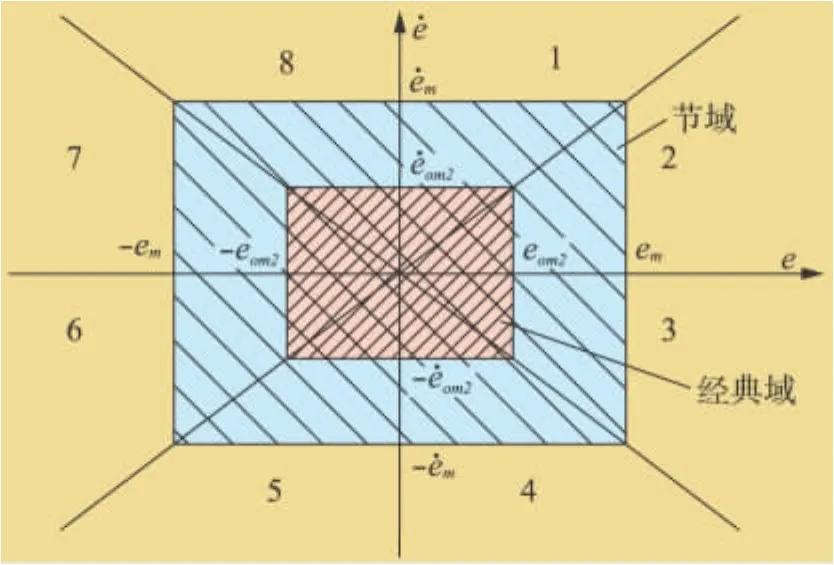
图2 特征模式与可拓集合
式中,S为关联度,M为测试模式,K(s)为特征状态关联函数经典域范围Rm为图2中深色阴影部分,即经典域A2;k1和k2分别为误差及误差变化率的加权系数。相应特征模式所取的不同值由控制系统本身决定,由该式便可计算出任意一点的关联度。
1.1.3 测度模式识别
特征平面内任一点S(e)的关联度用定量的形式反映其与可拓集合的关联程度,它既作为系统特征状态的一种度量,又起到了一种“路标”的作用,K(s)=0和K(s)=-1分别表示了合格与否以及可转变与否的分界,进而又可以用于划分测度模式。
(3)系统特征状态属于非域:测度模式M3=此模式下,特征量已经较远地偏离了经典域,控制过程中反映为控制失败或生产故障,无法通过改变控制变量的值使特征状态转变为经典域完全可控的状态,采取的措施为更换控制量或停止生产进行设备检修。
1.2 控制器输出
测度模式识别完成之后,可给出相应的控制策略,推理机制采用产生式规则,记为:IF测度模式;THEN控制模式。
1.2.1 测度模式 M1
特征量属于经典域,故可采用模糊推理与传统PID控制算法相结合的模糊PID控制策略,能够在线修正传统PID控制算法的3个参数,从而达到自适应的目的。其中传统PID控制算法为

式中,kp,ki,kd分别代表比例、积分、微分系数。
1.2.2 测度模式 M2
测度模式M2是可拓控制策略发挥作用的主要区域,控制器输出可采用文献[7]中提出的算法,这种算法克服了控制量完全取决于特征状态加权向量的问题。控制器输出为

其中,u(t)为当前时刻的输出;y(t)为当前时刻被控量的采样值;k为过程的静态增益;Kci为第M2i个测度模式的控制系数;K(s)为特征状态关联度;sgn(e)为偏差的符号函数,取
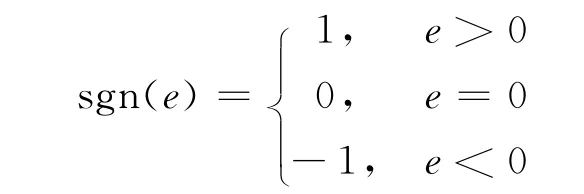
ε为小范围修正量,则
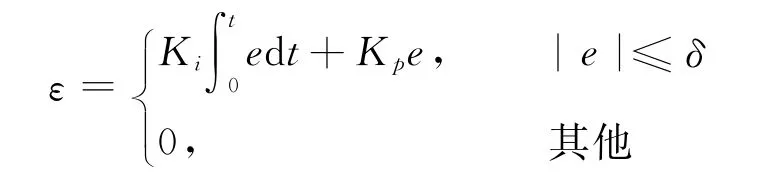
其中,δ为小正数;|e|≤δ时,ε的取法类似于PI控制算法,但整定要求不高,其作用是为消除扰动和过程增益k的不准确性[8-9]。
1.2.3 测度模式 M3
对测度模式M3,控制器输出取最大值。必须注意的是,此时系统处于既难以有效控制又难以转化的范围,控制器输出长时间处于最大值从某种程度上表明控制过程已经失败,对于控制策略而言,应避免这种情况的发生。综上所述,控制器的输出为

2 仿真研究
2.1 被控对象
选择的被控对象是染整工艺中圆网印花机的传动系统,工艺要求主传动系统中各电机协调工作,可考虑为各从动电机的转速与主令电机输出转速保持一致。将两者转速的偏差e与偏差变化率e·的范围记为基元B0,当B0⊂B1(即属于经典域A1)时,符合控制指标,印花工艺可平稳进行,此时控制器的输出保持不变,u(t)=u(t-1)。当遇负载扰动或者其他干扰时,两电机转速偏差发生变化,控制器对其调节。B0⊂B2(即属于经典域A2)时,模糊PID控制器能够取得良好控制效果;B0⊂B4(即属于非域A4)时,织物因张力过大发生断裂,生产失败,但为了避免这种失败的出现,当检测出B0⊂B5(即属于可拓域A5)时,即进入预警范围或危险区域,传统做法可以停止生产,对生产过程进行检修,排除故障。但实际上此时织物并没有断裂,生产上并没有失败,只是因为模糊PID控制方式不能将其迅速调节至控制指标容许范围内,存在生产失败的风险,这个范围即为可拓域,是可拓控制算法应用的最佳范围,可拓控制能够实现由模糊PID不能有效控制到能够有效控制这一矛盾的转化。
圆网印花联合机中所使用直流电机的部分额定参数为:额定电压Unom=220V,额定电流Inom=136A,额定转速nnom=1 460r/min,电枢电阻Ra=0.21Ω,转动惯量GD2=22.5N·m2,4极。励磁电压Uf=220V,励磁电流If=1.5A。通过电动势平衡方程和转矩平衡方程可以求出直流电机输出转速与输入电压之间简化的二阶传递函数模型[10]:

2.2 SIMULINK仿真框图
系统的可拓模糊PID控制模型在MATLAB/SIMULINK 中的所建立的仿真框图见图3[11-12]。

图3 可拓控制模型Simulink系统框图
图3中模块“Fuzzy Controller”(模糊控制器)与“Extension Controller”(可拓控制器)分别为模糊PID控制器与可拓模糊PID控制器,二者的具体结构见图4和图5。

图4 模糊控制器结构

图5 可拓控制器结构
2.3 仿真结果及分析
经过反复试验,可拓控制器中的各主要参数取为:eom2=0.15,e·om2=8;em=0.5,e·m=31.5,加权系数取k1=0.3,k2=0.7,过程增益k=135,控制系数Kci=23 800。仿真结果见图6。

图6 仿真结果
图6中绿色的单位阶跃输入为主令电机的转速,即从电机的参考输入;红色曲线为在模糊PID控制器下的响应曲线;蓝色曲线为可拓模糊PID控制器控制下的响应曲线。两者最终均能完成从电机对主令电机的速度跟随,但动态性能不同。可拓模糊PID控制策略下的响应速度更快,超调量更小,调节时间也更短;同时,对于0.5s时所加的幅值为8的脉冲扰动的调节,由于具备了模糊PID控制器的自适应能力,能很快地调节至稳定状态。仿真结果表明:可拓PID控制策略可有效地改善双电机同步传动系统的动态性能,并具有很好的抗扰能力。
3 结 语
可拓控制策略在处理非渐变、质变问题中具有其他控制算法难以比拟的优势,模糊PID控制策略的优势在于在处理量变问题,并具有自整定的能力。为结合两者的优势,本文提出了可拓模糊PID控制器对经典域进行了可拓变化,体现出的是矛盾的转化,并以染整工艺中的双电机同步传动系统为被控对象进行仿真。结果表明:该控制策略对改善同步传动系统的动态系统具有优良的作用。
[1]Li Jian,Wang Sienyu.Primary research on extension control[C]∥Information and Systems.Beijing.International Academic Publisher,1991,1:392-396.
[2]杨春燕,蔡 文.可拓工程[M].北京:科学出版社,2007.
[3]翁庆昌,陈珍源.非线性系统的自适应可拓控制器设计[J].中国工程科学,2001,3(7):54-58.
[4]何 斌,朱学锋.可拓自适应混杂系统[J].控制理论与应用,2005,22(7):165-170.
[5]王行愚,李 健.论可拓控制[J].控制理论与应用,1994,11(1):125-128.
[6]李士勇.模糊控制、神经网络控制和智能控制理论[M].哈尔滨:哈尔滨工业大学出版社,1996.
[7]潘 东,金以慧.可拓控制的探索与研究[J].控制理论与应用,1996,13(3):305-311.
[8]王明东,刘宪林,于继来.水轮发电机组调速系统的可拓控制 [J].水力发电学报,2009,28(4):171-186.
[9]Chen Zhenyuan,Weng Qingchang.A simple PIextension controller[J].Journal of Guangdong Univer-sity of Technology,2001,18(1):1-4.
[10]顾绳谷.电机及拖动基础[M].3版.北京:机械工业出版社,2003.
[11]Yu Biao,Zhu Hui.Water level control embedded fuzzy-PID and pole-placement strategy[J].Key Engineering Materials,2011,464,:43-47.
[12]刘金琨.先进PID控制 Matlab仿真[M].2版.北京:国防工业出版社,2004.
