基于RAGA的水稻敏感指数累积函数研究

杜宜霞

( 农垦查哈阳灌区水务局，黑龙江 甘南162116)

0 引 言

作物水分生产函数是指作物产量与水分之间的相互关系，由于水资源严重短缺，相应对农田灌溉用水管理水平要求更高，迫使人们更深入更广泛地进行作物水分生产函数的研究。以广泛应用的Jensen 模型为例，过去在研究敏感指数时，一般都将生育期划分为4个生育阶段，而实际应用水分生产函数时，一般都需要将作物的整个生育期划分为5个或6个甚至更多，则就不能直接采用原有敏感指数值，必须寻求借助于原有阶段划分情况下敏感指数来求解新的阶段划分下敏感指数的方法，敏感指数累积函数可在一定程度上解决这一问题。

1 敏感指数累积函数

前人在研究中发现，水分敏感指数在理论求解和实际应用中存在一个矛盾，即求解时希望阶段划分的少一些，因为阶段较多时常常出现水分敏感指数为负值的不合理现象;而在使用时，又希望阶段划分的多一些，以便更好地表示灌水对产量的影响。针对此矛盾，前人进行了大量研究，提出用敏感指数累积函数来解决这一矛盾，敏感指数累积函数是将阶段水分敏感指数累加值与相应阶段末的时间t 所建立的关系，即

式中:Z( t) 为第t 时刻以前作物各阶段水分敏感指数累加值，λ( t) 为阶段t 的水分敏感指数。

建立关系式(1) 之后，针对各种时段划分的情况，λ( t) 可用下式求得:

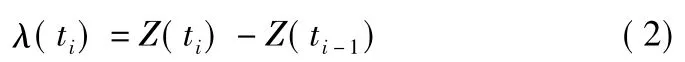
Jensen 模型的敏感指数λ 值越大，因缺水造成的减产量就越大。基于作物水分敏感指数的数值前期和后期小、中期大的特点，王仰仁［1－2］等提出了用生长曲线来拟合Z( t) ，即:

式中:A，B，C 为拟合参数。

2 敏感指数累积函数求解方法

2.1 方法介绍

敏感指数累积函数求解方法目前有两种，第一种是分步拟合法对式(3) 进行拟合，即先通过最小二乘法求得各阶段的水分敏感指数λ( ti) ，对λ( ti) 进行累加得Z( ti) ，然后用Z( ti) 和ti数据拟合式(3) 求得式中参数A，B，C。此外，文献［3］对分步拟合法进行了改进，提出了线性化求解方法［3］。

另一种是直接拟合法，以模型计算产量和实测产量误差平方和最小为目标，运用非线性规划技术，也是本文所使用的方法，由实测腾发量ET 和产量Y 直接拟合式( 3) ，相关公式如下:

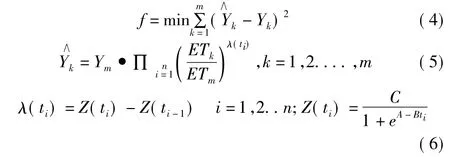
2.2 检验方法

拟合的复相关指数R 和相对误差ER( %) 分别用以下两式计算:

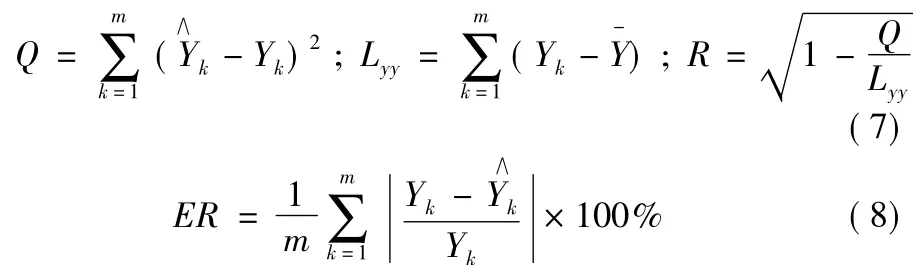
式中: Q，Lyy分别是剩余平方和和离差平方和，其它意义同上。

3 实码加速遗传算法求解敏感指数累积函数

3.1 实码加速遗传算法( RAGA) 寻优步骤

遗传算法( Genetic Algorithm，简称GA) 是模拟生物在自然环境中的遗传和进化而形成的一种自适应全局优化概率搜索算法，是一种新兴的非线性优化方法。主要过程包括选择、交叉和变异［4］。

例如求解如下最优化问题: min:f( X) ，sub to: aj≤xj≤bj具体求解步骤如下:

步骤1:在各个决策变量的取值范围内随机生成N 组均匀分布的随机变量。

步骤2:计算目标函数值，从大到小排列。

步骤3:计算基于序的评价函数。

步骤4:进行选择操作。

步骤5:对步骤4 产生的新种群进行交叉操作。

步骤6:对步骤5 产生的新种群进行变异操作。

步骤7:进化迭代。

步骤8:上述7个步骤构成了标准遗传算法，由于标准的遗传算法不能保证全局收敛性，在实际应用中常出现在远离全局最优点的地方即停止寻优工作，为此，可以采用第1 次、第2 次进化迭代所产生的优秀个体的变量变化区间作为新的初始变化区间，算法进入步骤1，重新运行标准遗传算法，形成加速运行，则优秀个体区间将逐渐缩小，与最优点的距离越来越近，直到最优个体的优化准则函数值小于某设定值或算法达到预定加速次数，结束整个算法运行，此时，当前个体中最佳个体指定为RAGA 的结果［4－5］。

上述8个步骤构成了基于实码的加速遗传算法( Real coded Accelerating Genetic Algorithm，简称RAGA) 。

3.2 敏感指数累积函数求解示例

根据文献［5］采用多年的水稻灌溉试验资料对水稻敏感指数累积函数的研究成果，拟合参数的A，B，C 范围全部符合以下要求，即A ∈(0，30) ，B ∈(0，0.3) ，C ∈(0，3) ，敏感指数A，B，C 即为RAGA 寻优时的决策变量，应用上述范围直接约束，目标函数为式(4) ，即可通过RAGA 寻优。

本文采用文献［5］1992 ～1996年南方双季早稻的试验资料，利用实码加速遗传算法进行拟合求解，并与文献［5］通过分步拟合方法的拟合结果进行了比较。拟合参数和拟合误差比较见表1 和表2。

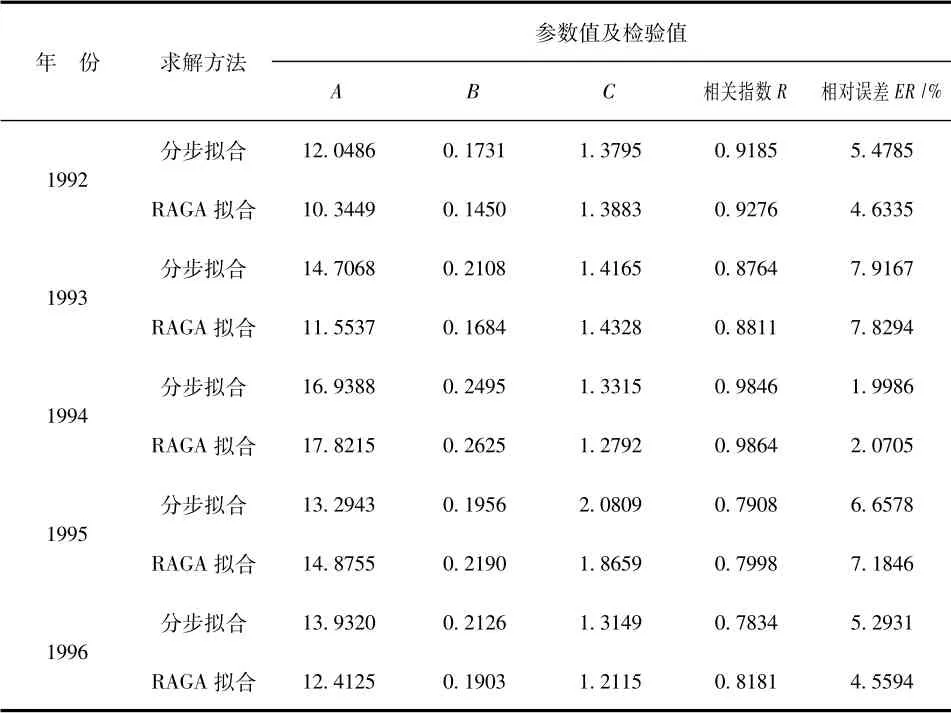
表1 RAGA 拟合与分步拟合误差比较表

表2 RAGA 拟合法相对误差与分步拟合法相对误差之间误差平方和

3.3 求解结果

1) 由表1 可知，实码加速遗传算法( RAGA) 和分步拟合两种方法所得到的拟合参数A，B，C 的值较为接近;从相关指数比较看，RAGA 拟合的R 值均比分步拟合的要大，拟合效果比分步拟合要好; 从相对误差比较来看，同样是RAGA 拟合相对更为精确，在5 a的相对误差中，有3 a是RAGA 拟合的相对误差小，只有1994年和1995年相对较大。

2) 从表2 可以看出，RAGA 拟合的相对误差和分步拟合的相对误差非常接近，说明了分步拟合敏感指数累积函数的方法是可行的和有效的。

3) 利用实码加速遗传算法直接拟合敏感指数累积函数的效果是可行且满足精度要求的，与分步拟合方法相比更具优越性。

4 结 论

利用实码加速遗传算法直接拟合水稻敏感指数累积函数，经过实例求解，表明该方法直接、计算简便，避免了分阶段求解水分敏感指数，只要在程序中输入各处理下的腾发量和产量，即可得到所求拟合参数;此外，该方法拟合精度相对分步拟合方法更高，在求解敏感指数累积函数中具有应用价值，为敏感指数累积函数的推广应用提供了新的更有应用价值的有效方法。

［1］王仰仁，荣丰涛，李从民，等. 水分敏感指数累积曲线参数研究［J］. 山西水利科技，1997(4) :20－24.

［2］王仰仁，雷志栋，杨诗秀. 冬小麦敏感指数累积函数研究［J］.水利学报，1997(5) :28－35.

［3］杨宝中，张运凤，徐建新，等. 水稻的Jensen 模型中敏感指数累积函数拟合公式的线性化研究［J］. 灌溉排水学报，2006，25(3) :38－40.

［4］付强，王立坤，门宝辉，等. 推求水稻非充分灌溉下优化灌溉制度的新方法［J］. 水利学报，2002(10) :39－40.

［5］茆智，崔远来，李远华. 水稻水分生产函数及其时空变异理论与应用［M］. 北京:科学出版社，2003:32－33，73－75.