基于免疫蛙跳算法的小波神经网络的水稻需水量预测

李 琳，隋树涛

(密山市富密灌区水利水保总站连珠山分站，黑龙江密山158300)

水稻是中国主要的粮食作物，约占全国粮食作物种植面积的28%，其生产状况直接影响着中国的粮食安全［1－2］。黑龙江省属寒地黑土稻作区，是国家重要的商品粮基地，而降水与水资源时空分布不均形成的缺水以及水稻种植面积的进一步扩大，直接影响水稻的稳产高产。因此，水稻需水量的准确测定与预测成为制定灌溉制度、水资源规划与管理的重要依据和关键，对高效节水农业的发展意义重大。目前，国内许多学者研究并发展了多种水稻需水量的预测方法，如刘倩等［3］从多个影响因子分析出发，得到的BP 神经网络模型较好的反应气象因子与水稻需水量之间的关系;付强等［4］应用多变量自回归模型建立了井灌水稻生育期内需水量预测模型，模型拟合与预测的效果良好; 冯艳等［5］以小波函数代替传统BP 网络中的S 型激活函数，建立了一种预测精度较高的水稻需水量预测的小波BP 网络模型。还有一些其他方法在需水量预测方面也取得了良好的效果。

本文提出了一种改进的免疫蛙跳算法( immune shuffled frog leaping algorithm，ISFLA) ，将该算法应用到小波神经网络( wavelet neural networks，WNN) 中，建立了对水稻需水量进行有效预测的基于免疫蛙跳算法优化的小波神经网络( ISFLA－WNN) 模型，并对水稻需水量进行预测。

1 免疫蛙跳算法的基本原理

1.1 混合蛙跳算法

混合蛙跳算法( shuffled frog leaping algorithm，SFLA) 是一种受自然生物模仿启示而产生的基于群体的协同搜索方法。对于D 维函数优化问题，第i 只青蛙可表示为U( i) =，根据每只青蛙适应值( 位置) 的大小按下降顺序排列，整个青蛙群体被分为m个子群体，每个子群体包含n 只青蛙，即青蛙数目为F = m·n。在每一个子群体中，适应值最好的个体和最差的个体记为Ub和Uw，整个青蛙群体的最优值记为Ug。在每次循环中，只提高最差个体的适应值。在混合蛙跳中最差适应值( 位置) 青蛙的计算过程中，蛙跳步长更新: Si= rand( ) ×( Ub－Uw) ;位置更新:Uw( k +1) = Uw( k) +Si; Smax≥Si≥－Smax，其中rand( )∈［0，1］( k = 1，2…，n) ，Smax是最大步长。如果计算后新的解较优，则用其替代最差个体，并且通过上式求全局最优解Ug。如果得到的解没有改进，那么随机生成新解取代所求个体的解，算法继续迭代直至迭代次数完毕［6－7］。

1.2 改进的免疫蛙跳算法

免疫蛙跳算法具有混合蛙跳算法的全局优化与局部细致搜索优点，可以优化连续问题和离散问题，具有较强的鲁棒性;同时，群体具有的免疫机制对群体进行控制和调节，把目标函数和制约条件作为青蛙群体的抗原，保证生成的青蛙群体直接与问题相关联，收敛方向得以控制; 对与抗原亲和力高的青蛙抗体进行记忆，并从中提取免疫疫苗对抗体群进行注射，保证抗体群在更新过程中的多样性，提高算法的效率，防止群体的退化。参照免疫算法和混合蛙跳算法的设计原理，下面给出具体实现步骤:

1) 步骤1:抗原输入。输入目标函数和各种约束作为免疫蛙跳算法的抗原。

2) 步骤2:针对F 只青蛙( 解) ，产生初始群体。生成初始抗体群N、促进记忆青蛙群N1、检测记忆青蛙群N2。

3) 步骤3:计算每只青蛙抗体适应度。青蛙群体的抗原和抗体V 之间的亲和力: axν= optν，其中optν表示抗原和抗体之间的匹配程度，本文用抗原和抗体之间的适应值函数fittness( ν) 来表示，即axν= fittness( ν) 。F个青蛙抗体的信息熵为:式中Hj( N) 为N个抗体第j 位的信息熵，Pij为个抗体中的第j位为数值ki的概率。抗体ν 和抗体w 的亲和力为: ayνw=1/(1 + H(2) ) ，抗体ν 的浓度cν为:

式中: Tact为一个预先确定的亲和力阈值。

4) 步骤4:免疫记忆青蛙群体更新。根据一定比例，从青蛙抗体群N 中选出亲和力高的抗体，用它们替换促进记忆青蛙群体N1中亲和力低的抗体; 将抗体群N 中亲和力低的抗体选入检测记忆青蛙群体N2，用它们替换检测记忆青蛙群体N2中亲和力高的抗体。

5) 步骤5:青蛙抗体群的促进与抑制。当记忆青蛙群体N1中抗体浓度的最大值cmax低于抗体浓度阈值th 时，记忆青蛙群体中的抗体处于多样化; 否则抗体趣于一致化，随机产生的新个体代替被淘汰的浓度大的个体。用检测记忆青蛙群体N2去检测N 中是否含有已搜索过的抗体( 即N2中记录的抗体) ，如果有就用随机青蛙抗体取代它。

6) 步骤6:将促进记忆青蛙群体N1与检测后的青蛙抗体群N 相结合生成新的青蛙抗体种群，将F 只青蛙按适应值降序排列分为m 子群体，对每一个子群体中的青蛙个体找出其最优个体和最差个体，在指定迭代次数内提高差个体的适应值，针对各个子群体，按适应值降序排列体，进行重新分配和混合蛙跳运算;

7) 步骤7:终止条件是否满足? 如果满足，结束迭代，否则转向Step3。

1.3 算法测试

求二元函数f( x，y) =sin23 πx +( x－1)2(1 +sin2πy) +( y－12) (1 + sin22πy) ，x，y 在［－10，10］区间内的最小值问题，它有900个局部最小点。分别采用SFLA 算法和ISFLA算法进行计算，采用MATLAB7.0 编程处理，选取青蛙总数F= 200 ，子群体数m = 20 ，子群体内更新次数为10，抗体浓度阈值th 为0.85，计算得出在相同循环次数时，ISFLA 算法的精度高于SFLA 算法，表明ISFLA 算法比SFLA 算法收敛速度更快、精度更高。计算结果见表1。

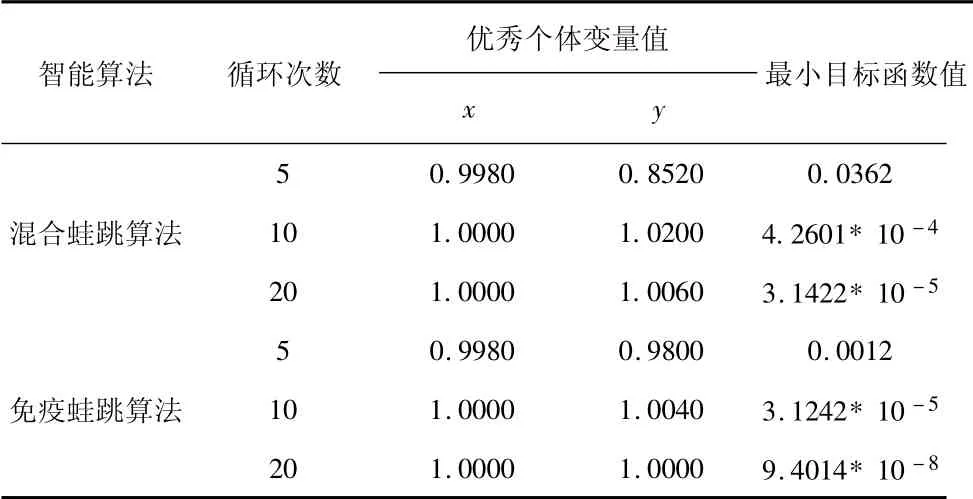
表1 计算结果对比表

2 基于ISFLA 优化的WNN 预测模型

2.1 WNN 模型的原理与结构

小波神经网络［8－9］是一种结合小波分析和神经网络而提出的一种前馈神经网络。一般的WNN 模型用小波函数代替Sigmoid 函数作为隐含层的激活函数，既具有神经网络的学习能力、泛化能力及非线性映射能力，又具有小波变换的多尺度时频分析手段和良好的逼近特性。本文采用只含有一个隐含层的3 层网络。网络的隐层神经元采用小波函数做激励函数，输出层神经元采用Sigmoid 函数做激励函数。

设输入的样本的个数为m，输入层节点的个数为p，隐含层节点的个数为n，输出层节点的个数为q; wij为连接输出层节点与隐含层节点的连接权值，wjk为连接隐含层节点与输入层节点的连接权值，θj为隐含层节点的阈值，θi为输出层节点的阈值，aj和bj分别为第j个隐含层节点的伸缩系数和平移系数;则上述WNN 模型可表示为:

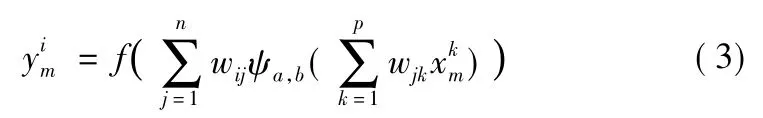
式中: f( x) 为Sigmoid 函数，即f(x) = 1/［1 + exp(－ x) ］。

由于Morlet 小波基对干扰的鲁棒性好、误差小、计算稳定等特点［10］，ψ( x) 采用较多使用的Morlet 母小波

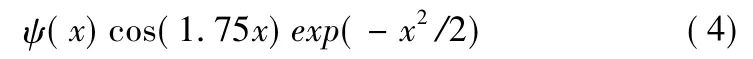
单结点输出时，网络输出的均方误差( mean square error，MSE) 为

WNN 模型采用梯度下降法训练网络，利用前馈网络反向传播误差，不断地调整、优化、确定网络的权值和尺度因子、平移因子，节点之间的权重值与阈值，使网络计算输出与期望输出拟合最优，即MSE 最小。

2.2 ISFLA－WNN 模型的实现

2.2.1 确定算法的参数

根据WNN 模型的输入输出样本集确定网络的拓扑结构并作规范化处理，对优化的网络参数进行编码，将神经网络的各连接权值、各阈值、伸缩平移系数作为青蛙个体。

2.2.2 初次优化网络参数

利用免疫蛙跳算法对WNN 模型参数( 权值、阈值、伸缩平移系数) 进行初次优化，代替了神经网络参数初始的随机赋值，克服了仅凭借误差的传播作为修正法则的弊端。

2.2.3 适应值评价

根据ISFLA 算法，以WNN 模型的均方差MSE 作为青蛙种群搜索性能的评价指标，适应度越高，网络实际输出和期望输出的误差越小，记录最佳个体适应度值，及其对应的青蛙个体，该青蛙个体就是下次迭代中WNN 模型的最优网络参数。

2.2.4 判断中止条件

判断适应度值是否达到最大误差设定值以及迭代次数是否达到最大迭代步数，若不满足条件，按免疫蛙跳算法进行更新，并生成新一代种群，返回(2) ;如果满足条件，将全局最优青蛙个体映射为WNN 网络的权值、域值、伸缩平移系数，得到一个建立好参数的WNN 网络。

2.2.5 进行WNN 模型操作，生成最优解

将上述方法得到的最优解作为WNN 网络的初始权值、域值、伸缩平移系数，对这些参数用WNN 模型的梯度下降法进行二次优化训练直到网络达到性能指标，经过以上训练，改进的免疫蛙跳算法优化的小波神经网络达到最佳状态，将该状态下的最终网络参数用于水稻的需水量预测，输出预期结果。

3 ISFLA－WNN 模型的应用实例

3.1 模型应用实例

本文选用文献［11］中的实测数据，即三江平原腹地—富锦市1985—1999年的观测资料来计算水稻的需水量。选择1985年—1998年的日平均气温T、日照时数h、风速u、饱和差d、和天然水面蒸发量E 作为输入变量，水稻需水量ET 作为单输出变量，1999年的水稻需水量留为检验样本集。根据输入样本水稻需水量及其相关影响因子，确定网络的输入层结点为5，输出层结点个数为1，隐含层结点个数为10，经训练后误差精度达到0.01，拟合程度较好，所以网络结构为5－10－1。选取青蛙总数F = 200 ，子群体数m = 20 ，子群体内更新次数为10，抗体浓度阈值th 为0.85。

3.2 预测结果分析

用归一化处理后的样本对ISFLA—WNN 模型和传统的WNN 模型的网络分别进行学习与训练，经过设定训练次数后，网络达到精度要求，误差收敛到期望值。对1999年水稻需水量进行预测检验，ISFLA—WNN 模型预测结果与传统的WNN 模型预测结果对比分析见表2，ISFLA—WNN 模型的拟合曲线见图1。

表2 WNN、ISFLA－WNN 模型预测效果比较

分析结果表明，ISFLA－WNN 模型的预测值、均方误差优于传统的WNN 模型; ISFLA－WNN 模型的水稻需水量网络预测结果与实测结果十分吻合，表明该模型具有较高的准确性，可对生产实践提供更为准确的理论依据。从整体分布可以看出，拔节孕穗期为水稻的需水临界期，水稻自身的生长对需水量影响较大，ISFLA－WNN 模型与WNN 模型在拔节孕穗期预测值的均方误差大于其它生育期预测值的均方误差，表现出影响水稻需水量因素的复杂性和多变性，在今后的水稻需水量预测模型中不但要考虑气象因素的影响，还加入水稻不同生育期的水分敏感指数，使预测预报模型更加全面、完善。

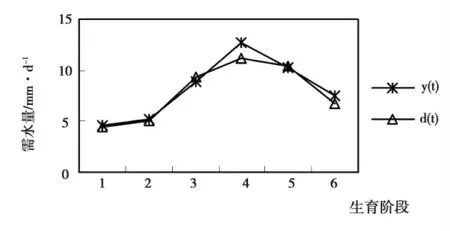
图1 1999年水稻需水量的实测值与预测值拟合图

4 结 论

免疫蛙跳算法( ISFLA) 在混合蛙跳算法的基础上将免疫算子应用于混合蛙跳算法的进化中，引入了免疫调节机制，保持了青蛙群体的多样性，在一定程度上防止个体退化，避免局部收敛，提高全局搜索能力和收敛速度。用ISFLA 优化WNN 模型的连接权值、阈值、伸缩平移系数，建立了ISFLAWNN 的水稻需水量预测模型，与传统的WNN 模型相比较具有更快的收敛速度和更高的预测精度，在水稻需水量预测方面具有较高的可靠性，为制定科学的水稻节水灌溉制度提供了强有力的理论依据。

［1］刘小军，曹静，李艳大，等. 水稻水分精确管理的知识模型研究［J］.中国农业科学，2010，43(8) :1571－1572.

［2］方福平，程式华.论中国水稻生产能力［J］.中国水稻科学，2009，23(6) :559－560.

［3］刘倩，熊丽荣.基于人工神经网络算法对水稻需水量的预测［J］.华中农业大学学报，2007，26(6) :885－887.

［4］付强，王志良，梁川.多变量自回归模型在三江平原井灌水稻需水量预测中的应用［J］.水利学报，2002(8) :107－112.

［5］冯艳，付强，李国良.水稻需水量预测的小波BP 网络模型［J］. 农业工程学报，2007，23(4) :66－69.

［6］王辉，钱锋. 群智能优化算法［J］. 化工自动化及仪表，2007，34(5) :10.

［7］吴华丽，汪玉春，陈坤明，等.基于混合蛙跳算法的成品油管网优化设计［J］. 石油工程建设，2008，34(1) :15.

［8］曹大有.一种免疫粒子群优化算法及在小波神经网络学习中的应用［J］. 计算机应用于软件，2009，26(6) :189－191.

［9］毛鸿伟，潘宏侠，刘文礼.基于粒子群优化的小波神经网络及其在齿轮箱故障诊断中的应用［J］. 振动与冲击，2007，26( 5) : 133－134.

［10］李界家，李世涛，王丽娜.基于遗传小波神经网络的故障预报应用［J］. 沈阳建筑大学学报( 自然科学版) ，2009，25( 2) : 381－382.

［11］付强.农业水土资源系统分析与综合评价［M］.北京: 中国水利水电出版社，2005:126－128.