基于Frank Wilcoxon秩和检验的多元统计分析在酿酒葡萄分级中的应用*
2012-10-24吴海燕
吴海燕
(哈尔滨德强商务学院)
0 引言
随着人们生活水平的日益提高,葡萄酒现今已融入千家万户,所以对葡萄酒质量的评价显得尤为重要.而酿酒葡萄的好坏直接影响到葡萄酒的质量,如何根据所酿葡萄酒的质量及酿酒葡萄的理化指标对酿酒葡萄进行分级随之成为大家关注的问题.利用2012全国数学建模竞赛A题所提供的某一年份一些葡萄酒的评价结果及该年份这些葡萄酒和酿酒葡萄的成分数据,采用统计学中的Frank Wilcoxon秩和检验和多元统计分析方法对酿酒葡萄进行了分级.
该文第一部分利用Frank Wilcoxon秩和检验对两组评酒员的评价结果的差异性进行了判别,Frank Wilcoxon秩和检验无需验证样本所在的总体是否服从正态分布,检验理论简单,过程计算量小,是统计学中一种有效且方便的假设检验方法.鉴于两组评酒员的部分评价结果存在差异性,第二部分对两组葡萄酒样品评价结果的变异系数进行了比较,变异系数的确定只需计算各组样品对应的均值及方差,为结果可信性的验证带来了方便,最终得出第二组评价结果的可信度更高.第三部分考虑到酿酒葡萄的理化指标多达60多项,部分理化指标之间可能存在相关性,所以首先利用主成分析法从中提取主成分,再将葡萄酒的质量作为一级指标,采用聚类分析法,利用SPSS软件对酿酒葡萄的进行了分级,最后的数值结果对比说明了方法的有效性.
1 Frank Wilcoxon秩和检验在葡萄酒评价结果是否具有显著性差异判别中的应用
Frank Wilcoxon秩和检验是统计学中一种有效且方便的检验方法,它无需考虑样本来自的总体是否为正态总体,所以适用范围较广.
1.1 秩和检验的原理及步骤
步骤1 在显著性水平α=0.05的条件下,对检验假设H0:μ1= μ2,H1:μ1≠μ2进行检验,其中μ1,μ2分别为两个总体的均值.
步骤2 对两组样本数据进行编秩.即将两组评酒员对每个样品的评价结果的总分作为两个总体的样本,n1,n2分别为第一组和第二组的样本容量.将两组样本值混合后按照从小到大的次序编号排列成如下形式:x1<x2<… <xn,其中 x1的下标 i即为 xi的秩,i=1,2,…,n,n=n1+n2.为了结果的可靠性,若遇到样本值相同的情况,对这些样本的秩的定义为下标的平均值.
步骤3 求样本值的秩和及其分布.鉴于n1=n2,该文选取求第一组样本值的秩和,记为R1,R1的观测值记为r1.由Frank Wilcoxon秩和检验的理论可知当H0为真时,R1近似服从正态分布 N(μR1,),其中
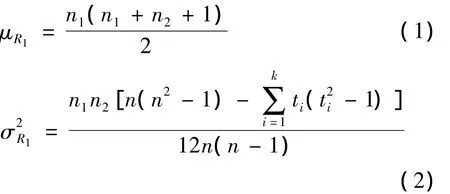
k表示秩相同的组的个数,ti(i=1,2,…,k)表示第i组中具有相同秩的样本的个数.
1.2 两组评价结果是否具有显著性差异判别举例及最终结果
例1 以红葡萄酒的样品1为例,对两组的评价结果是否具有显著性差异进行判别.
解 首先将两组样本值混合,按自小到大的次序排序,得出各样本值的秩见表1.

表1
由(1)和(2)式得μR1=10×21/2=105,=174.7.当 H0为真时,近似地有 R1~N(105,174.7),拒绝域为1.96.现在R1的观察值为r1=89,得=1.16<1.96,故接受H0,认为两组评酒员的评价结果无显著性差异.
例1针对红葡萄酒的样品1具体给出了评价结果是否具有显著性差异的判别结果.为了说明方法的有效性,利用C语言编程计算出了剩余的红葡萄酒和白葡萄酒的样本的评价结果是否有显著性差异的判别结果.结果显示:28个白葡萄酒的样品中,仅有2个样品的评价结果有显著性差异,其余26组均无显著性差异;27个红葡萄酒的样品中,有7个样品的评价结果有显著性差异,其余的20组均无显著性差异.
鉴于部分结果存在差异性,下面将对两组评价结果的可信性进行分析,以判别用哪组评价结果作为葡萄酒质量的衡量标准.
2 两组评价结果的可信性分析
鉴于所给评价结果数据是两组评酒员分别对每个样品的澄清度、色调、纯正度、浓度、质量、纯正度、浓度、持久性、质量和平衡 /整体评价等方面分别打分,再求和得到总分,所以该文通过对反映每个样品品质的参数求变异系数,再将各参数的变异系数求和得到该样品的变异系数.变异系数越大,可信度越低;变异系数越小,可信度越高.下面以红葡萄酒样品13为例对其变异系数做详细分析:
设 αij(i=1,2,…,20;j=1,2,…,10)表示第i个评酒员对第j个参数的评分,(i=1,2,…,m为第一组的分数,剩余的为第二组的分数),则样品第j个参数得分的真值为,样品第j个参数得分的真方差为DEj)2,样品第j个参数的变异系数为
通过Excell数据整合处理,得到了红葡萄酒样品13的各参数的变异系数,见表2.
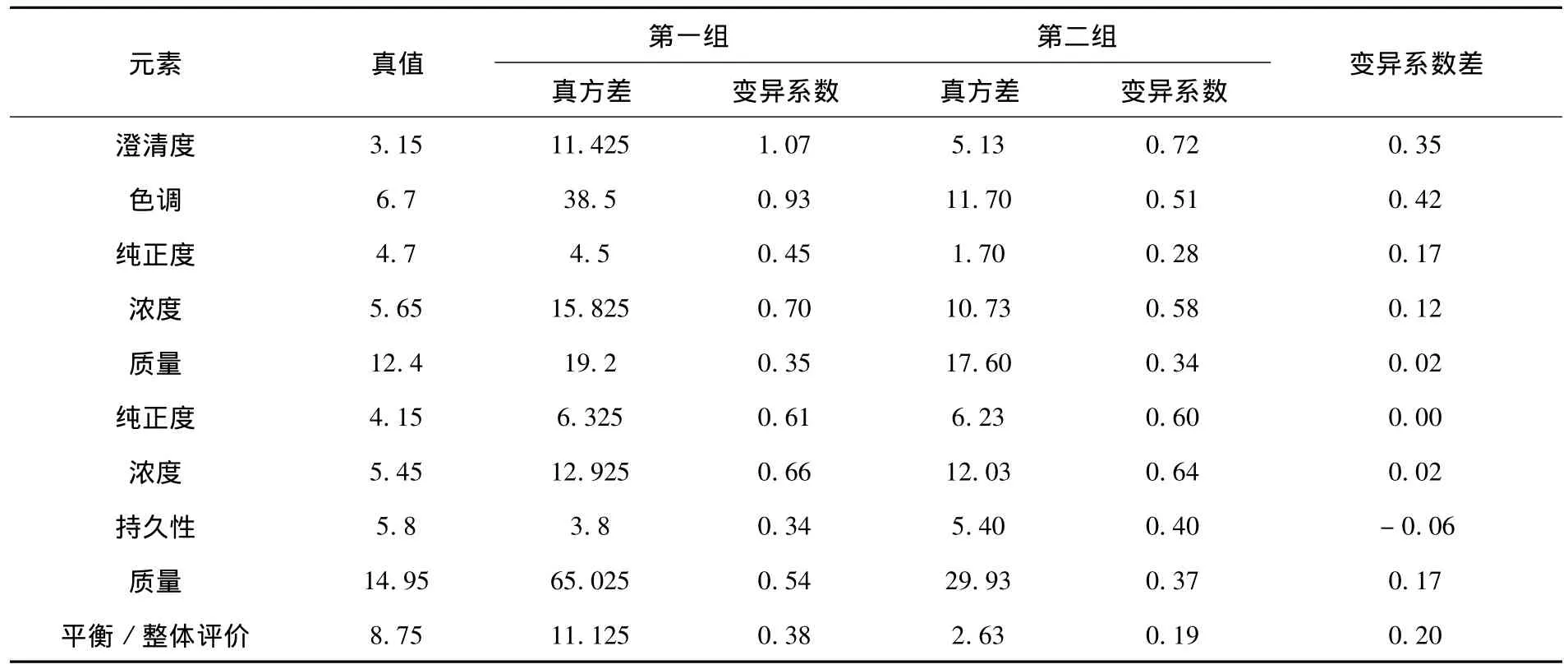
表2 红葡萄酒样品13的各参数的变异系数对照表
每个样品评价结果的变异系数为其各参数变异系数之和.为了使结果更有说服力,更直观的说明两组评价结果变异系数的大小关系,将两组红白葡萄酒样品的变异系数值用Excell生成图的形式表示,见图1和图2.
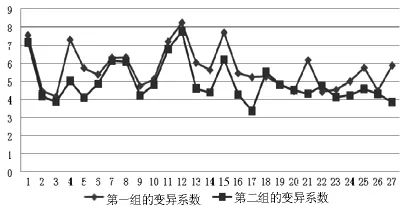
图1 两组红葡萄酒样品的变异系数对照图
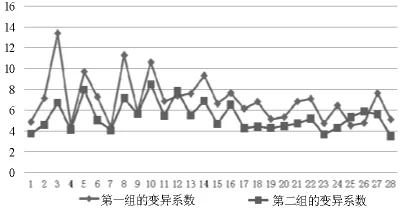
图2 两组白葡萄酒样品的变异系数对照图
显然,红白葡萄酒样品的评价结果均为第二组的变异系数较小,可信度更高,所以下面将以第二组的评价结果作为葡萄酒质量的衡量标准,进一步对酿酒葡萄进行分级.
3 主成分分析和聚类分析方法在酿酒葡萄分级中的应用
鉴于本部分要对酿酒葡萄进行分级,而影响到酿酒葡萄质量的理化指标变量多达五六十个,所以首先考虑应用主成分分析的方法,筛选出理化指标变量中的主成分.再对新得到的主成分变量进行系统聚类分析和均值聚类分析,进而对酿酒葡萄进行分级.下面首先根据两种方法的原理,建立该文的相关数学模型,随后利用统计分析软件SPSS来选出主成分,再利用已经标准化的原来指标计算出红和白酿酒葡萄样品的主成分的参数值,进而对其进行聚类分析,得到酿酒葡萄的分级结果.
3.1 主成分分析的原理及相关数据结果
3.1.1 主成分分析的原理
主成分分析法的核心思想是在力求数据信息丢失最少的前提下,对高维变量空间进行降维处理,即经线性变换后,以少数新的低维综合变量取代原始高维变量.具体步骤如下:
步骤1 数据标准化,将酿酒葡萄的理化指标对应的原始数据变量 xi,i=1,2,…,63 经Excell简单处理后,再对其进行标准化处理,即zi,其中,Si分别为xi的样本均值与样本标准差.
步骤2 求样本的相关系数矩阵R,R应为63阶的对称矩阵,且对角线上的元素均为1.
步骤3 求样本的相关系数矩阵R的特征值λi,i=1,2,…,63,其中λ1≥λ2≥…≥λm≥…≥0.
步骤4 求λi对应的标准化特征向量li,i=1,2,…,63.
步骤5 选定主成分的累计贡献率的标准,以大于或等于80%为宜,来定主成分中变量的个数m.
步骤6 最后得到主成分为yi=,i=1,2,…,m.
3.1.2 相关数据结果
以主成分的贡献率85% 为标准,对主成分进行抽取,通过SPSS软件分析后得到红葡萄的主成分个数为12个,白葡萄的主成分个数为13个.即可以分别用12和13个新的变量来表示原来红葡萄和白葡萄的63个对应的理化指标.在进行分析的过程中,同时得到了样本的相关系数矩阵特征值的碎石图(如图3)和主成分累计贡献率的选取标准(以红葡萄为例,见表3).
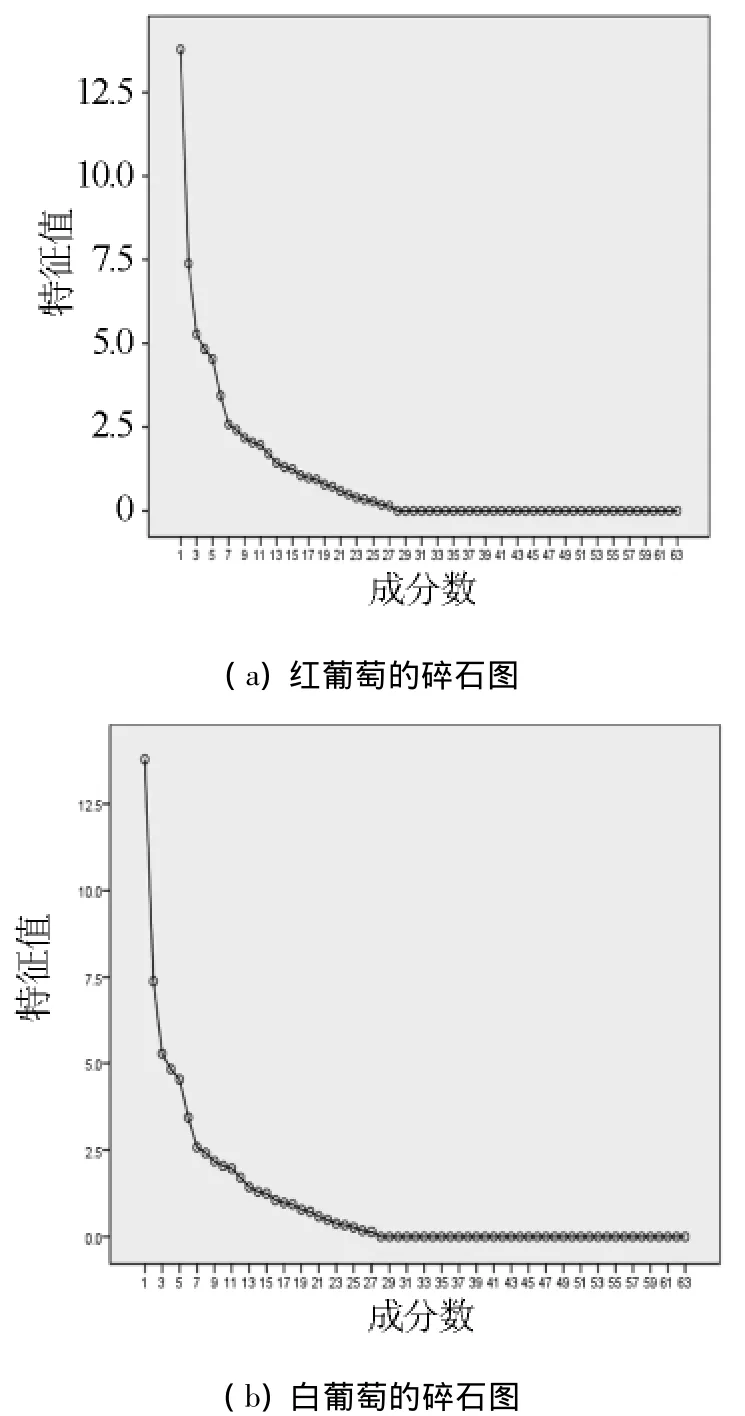
图3 红、白葡萄样品经主成分分析后得到的相关系数矩阵特征值的碎石图
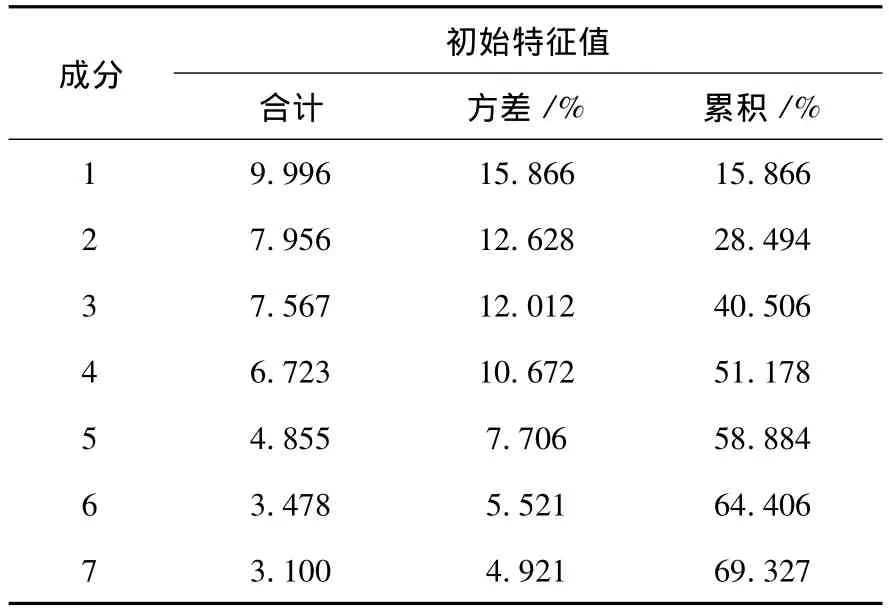
表3 红葡萄的主成分的累计贡献率与成分个数选取的对比
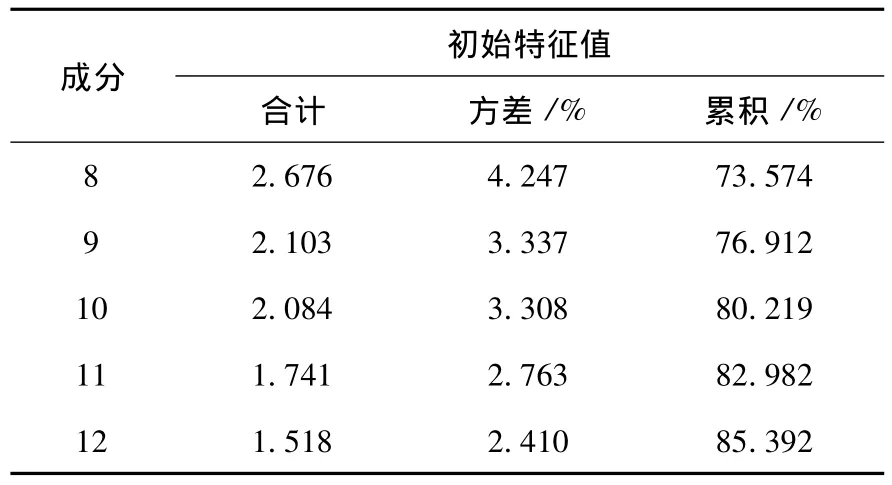
续表
3.2 系统聚类分析法的原理及相关数据结果
3.2.1 系统聚类分析的原理
系统聚类分析法是较常用的一种聚类方法,其基本思想是:首先将每个样本各视为一类,定义类与类之间的距离,将距离最短的两类合并为一个新类;再计算新类与其他类之间的距离,将距离最短的两类合并为一个新类.如此下去,直到所有样本全部合并为一个大类为止.最后,再根据事先给定的分类临界值,确定分类,具体步骤如下:
步骤1 计算样本两两之间的距离.
步骤2 将每个样本各作为一类.
步骤3 将距离最近的两类合并为一个新类.
步骤4 若类的个数等于1,转为步骤5.否则,计算新类与其他各类之间的距离,转为步骤3.
步骤5 画聚类图.
步骤6 根据给定的分类临界值,确定最终分类结果.具体的分类原理结构聚类图(以白葡萄的聚类分析图为例,如图4所示).
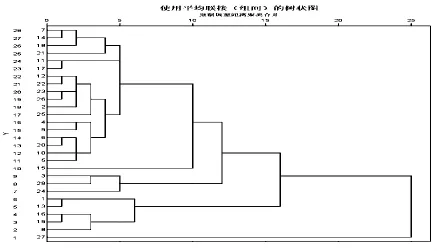
图4 白葡萄聚类分析的聚类图
3.2.2 酿酒葡萄的分级结果
根据主成分分析法得到的主成分数据,同时将葡萄酒的质量的评价结果作为一级指标利用聚类分析法对酿酒葡萄进行了等级划分.下面是在临界值为4(即将酿酒葡萄分为4类)的条件下进行分级得到的结果:
红葡萄:{3,5,6,11,17,18,23}、{2,8,14,16,19,20,21,22,27}、{10}、{1,4,7,9,12,13,15,24,25,26}.
白葡萄:{1,8,13,15,16,18,19}、{27}、{3,24,28}、{2,4,5,6,7,9,10,11,12,14,17,20,21,22,23,25,26}
当然,只要事先选定一个临界值,分级的结果就会有所调整,但总的方向是一致的.
4 结论
该文基于Frank Wilcoxon秩和检验,根据2012全国数学建模竞赛A题所提供的某一年份一些葡萄酒的评价结果及该年份这些葡萄酒和酿酒葡萄的成分数据,利用主成分分析及聚类分析对酿酒葡萄进行了分级,相关数值结果得到了专家的认可,获得了省级一等奖.
[1] 盛骤,谢式千,潘承毅.概率论与数理统计第4版[M].北京:高等教育出版社,2008.
[2] 吴孟达,成礼智,吴翊,等.数学建模教程[M].北京:高等教育出版社,2011.
[3] 区靖祥,邱建德.多元数据的统计分析方法[M].北京:中国农业科学技术出版社,2002.
[4] 贺昌政,张九龙,林嫔.基于数据分组处理方法的聚类分析模型[J].系统工程学报,2008,23(2):222-237.
[5] 李云,刘霁.神经网络与主元分析在采矿工程中的应用[J].中南林业科技大学学报,2010,30(6):139-146.
