椭圆曲线上的向量空间秘密共享方案

才宇飞，姜 伟，刘焕平

(1.哈尔滨师范大学;2.天津市渤海石油第一中学)

0 引言

在保密通信中，秘密共享是信息安全和数据保密的重要手段，针对密钥管理中密钥的泄漏问题和遗失问题，Blakley［1］和 Shamir［2］于 1979 年分别独立提出了门限秘密共享体制，由于门限秘密共享体制简单有效和易于实现，因此得到了很多学者的关注并对其进行了大量的研究.Asmuth和Bloom［3］提出了基于中国剩余定理的秘密共享方案，相对于Shamir［2］的方案降低了秘密重构阶段的计算复杂性，同时安全性也降低了.Angsuman Das 和 Avishek Adhikari［4］提出一般接入结构上的秘密共享方案，使其具有更加广泛的应用空间.1989 年，Brickell［5］提出了向量空间秘密共享方案，并且指出Shamir门限方案是向量空间秘密共享方案的特殊情况.2002年，许春香［6］等人提出一个密钥空间为有限域的安全矢量空间秘密共享方案，并对安全性和信息率做了定量分析.

由于现代密码分析技术的不断发展，攻击者的计算能力增强，基于有限域的密码体制已经不能满足安全性的需要，越来越多的学者投入到安全性更好的椭圆曲线密码体制的研究，由于椭圆曲线公钥密码体制具有密钥短，加密强度高，存储空间小的优点，学者构造了许多的椭圆曲线秘密共享方案［7-9］.

1 预备知识

1.1 向量空间访问结构及向量空间秘密共享方案

设 P={p1，p2，…，pn}是n个分享者集合，K=GF(q)是一个有限域，分发者D∉P，Kr是K上的r维向量空间.Γ是P上的一个单调访问结构，且r不小于所有最小授权子集的最大基数.称Γ是一个向量空间访问结构，如果存在函数

φ:P∪D→Kr，满足性质φ(D)=(1，0，…，0)∈〈φ(pi):pi∈B〉⇔B∈Γ.

向量空间秘密共享方案［10］构造如下:首先D向全体参与者公布函数φ，对要共享的秘密S∈K，D定义v1=S，并随机地选取vi∈K，i=2，3，…，r.K 中的一个向量 v=(S，v2，…，vr)，使得 S=v·φ(D).其中 φ(D)=(1，0，…，0)，把si=v·φ(pi)的值作为子秘密份额秘密发送给每个参与者pi，如果B={p1，p2，…，pl}是一个授权子集，则存在K中的一个向量λ =(λ1，λ2，…，λl)，满足，其中“·”表示向量的数量积(内积)，则有

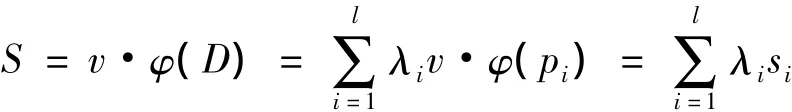
从而对于B中的参与者来说，秘密S由他们所共享的子秘密si的线性组合来恢复.

1.2 模素数的椭圆曲线

定义1 有限域Zp上的椭圆曲线E(Zp)是定义在仿射平面上的三次方程y2≡(x3+ax+b)modp的所有解(x，y)∈Zp×Zp与无穷远点O构成的并集，记为

其中:p为素数，p ＞ 3，a，b∈Zp，且4a3+27b2≠0.

E上的点数记为#E，它满足不等式E上的加法运算定义如下:假设P=(x1，y1)，Q=(x2，y2)是 E 上的点.如果 x1=x2且y2=-y1，则 P+Q=O;否则 P+Q=(x3，y3)，

其中

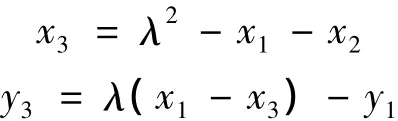
且

可以证明，椭圆曲线上的点关于点的加法构成阿贝尔群.

如果P=(x，y)，k是一个整数，那么

点P的阶是满足nP=O的最小的正整数，记为l.

定义2 给定一个有限域Zp上的椭圆曲线E(Zp)，P∈E(Zp)，点P的阶为大素数l，对于给定点 R ∈〈P〉，计算整数n∈［1，l］，满足 nP=R.称为椭圆曲线离散对数问题(ECDLP).

2 椭圆曲线上的向量空间秘密共享方案

假设 P={p1，p2，…，pn}是n个参与者的集合，E(Zp)是有限域Zp上的椭圆曲线，G是一个l(l是一个大素数)阶的E(Zp)上的基点，且〈G〉上的椭圆曲线离散对数问题是难解的.所要共享的秘密S∈E(Zp)，Γ是P的一个向量空间访问结构，φ:P∪ D→是相应的函数，公开参数φ(pi)=(ai1，ai2，…，air)，φ(D)={1，0，…，0}.首先每个参与者pi选取 ai∈［1，l］，计算βi=aiG，ai作为私钥，βi公开.其次分发者D选取a∈［1，l］，计算 β =aG，a作为私钥，β 作为公钥，分发者要保证 βi≠ βj(i≠ j)，β ≠ βi，i，j=1，2，…n.

2.1 秘密份额的分发

(1)分发者D任意选取数x2，…，xr∈，令v=(S，x2G，…，xrG)∈ (Zp× Zp)r，所共享的秘密 S=v·φ(D).

(2)分发者计算 si=v·φ(pi)=ai1S+ai2x2G+ … +airxrG，i=1，2，…，n，si为参与者pi的子秘密共享.

公开 C1，C2i，i=1，2，…，n.

2.2 秘密的恢复

为了恢复秘密S，不妨假设B={p1，p2，…，pl}是授权子集，则存在Zp上的向量

又因为C2i-aiC1=si(见后文可行性分析)，所以授权子集中的成员用自己的私钥ai即可求得si，再由B中的所有参与者提供的子秘密si就可恢复秘密S，

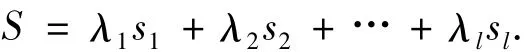
3 方案分析

(1)可行性分析.

令 xiG=(mi，ni)，i=2，…，r则向量

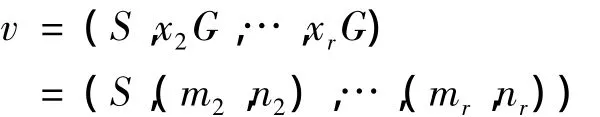
参与者共享的秘密

恢复秘密时，设授权子集 B={p1，p2，…，pl}∈Γ，则，其中λ =(λ1，λ2，…，λl)，由于所以授权子集中的成员用自己的私钥ai即可求得 si，秘密

(2)本方案的安全性是基于椭圆曲线离散对数问题难解性及椭圆曲线上的Elgamal密码体制的安全性.采用椭圆曲线上的Elgamal密码体制对子秘密si进行加密，提高了安全性能，计算简单.已知C1，试图从C1=kG中得到整数k是不可能的，同样，已知 C2i，试图从 C2i=si+kβi中得到si是不可能的，因为k是未知的.

(3)当要保存新的秘密S'时，只需分发者D重新选择xi∈R(Zp)*，i=2，…，r再计算参与者的子秘密si'，按照以上的步骤进行，公开C1'，C2i'.而不需要改变分发者和参与者的公钥和私钥.

4 结论

基于椭圆曲线提出了一个更具安全性，实用性的向量空间秘密共享方案.无需安全信道传输，也减少了通信代价.椭圆曲线密码体制使秘密共享建立在椭圆曲线离散对数难题上，提高了安全性能.再接下来的研究中，会考虑无可信中心的秘密共享方案.

［1］ Blakley G R.Safeguarding Cryptographic Keys［A］.Proc.AFIPS 1979 National Computer Conference，1979:313-317.

［2］ Shamir A.How to Share a Secret［J］.Communications of the ACM，1979，22(11):612-613.

［3］ Asmuth C.，Bloom J.A Modular Approach to Key Safeguarding［J］.IEEE Transactions on Information Theory，1983，29:208-210.

［4］ Das A.，Adhikari A.An Efficient Mult-use Multi-secret Sharing Scheme Based on Hash Function［J］.Applied Mathematics Letters，2010，23:993-996.

［5］ Brickell E F.，Some Ideal Secret Sharing Schemes［J］.Journal of Combinatorial Mathematics and Combinatorial Computing，1989，9:105-113.

［6］ 许春香，陈凯，肖国振.安全的矢量空间秘密共享方案［J］.电子学报，2002，30(5):715-718.

［7］ 殷春梅，汪彩梅.一种基于椭圆曲线的多密钥共享方案［J］.合肥工业大学学报，2006，29(4):392-394.

［9］ 肖立国，钟诚，陈国良.基于椭圆曲线密码体制的动态秘密共享方案［J］.微电子学与算机，2002(1):30-31.

［10］Stinson D R.密码学原理与实践［M］.冯登国等译，3版.北京:电子工业出版社，2010.