基于拟单边Lipschitz条件的非线性系统观测器设计

徐铭鞠，徐明跃

(哈尔滨师范大学)

1 状态描述

在过去的数十年中，非线性系统的观测器设计问题是一个非常积极的领域，出现了大量这方面的文献专著.非线性系统的状态观测器可以分为全维观测器和降维观测器.降维观测器只需估计与系统输出独立的部分状态即可.因此，和全维观测器相比，维数得以降低，即降维观测器可以由较少的积分器构成进而使整个控制系统变得相对简单.一般而言，非线性系统观测器的设计有两种方法.第一种是基于一种非线性状态变换，令动态误差系统线性化，因此设计状态观测器需运用到线性技术.第二种方法是则是不需要进行变换，直接基于原始的系统进行观测器设计［1-3，5-6，8-10］.

为便于叙述，本文引入如下记法:

考虑如下的一类Lipschitz非线性系统:

其中 x∈Rn，u∈Rm，y∈Rp，A∈Rn×n，C ∈Rp×n，Φ(x，u):Rn→Rn关于x是非线性的.

笔者总是假定(A，C)可观测，并且C是行满秩的.

定义1.1 对于n维的向量函数Φ(x，u)，如果存在常数γ使得

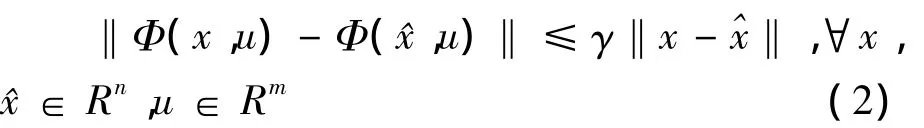
则 γ称为 Φ(x，u)关于 x的 Lipschitz常数.称Φ(x，u)是关于x的Lipschitz非线性函数.对于n维的向量函数Φ(x，u)，如果存在正定矩阵P和依赖于P的常数vp使得

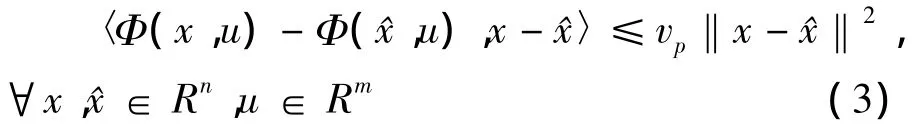
则vp称为Φ(x，u)关于x的单边Lipschitz常数称Φ(x，u)是关于x的单边Lipschitz非线性函数.

对于n维的向量函数Φ(x，u)，如果

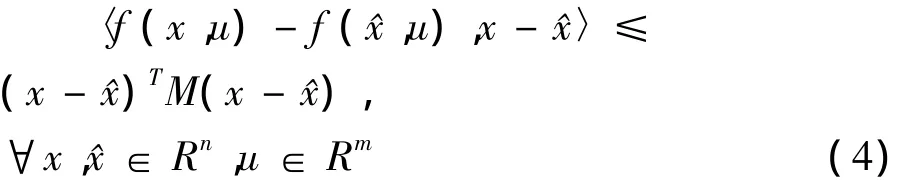
其中f(x，u)=PΦ(x，u)，P是待求正定阵，M是一个实对称矩阵(不必负定或正定)称为PΦ的带有拟单边常数矩阵.称Φ(x，u)是关于x的拟单边Lipschitz非线性函数［6］，不等式(2)，(3)和(4)分别叫做Lipschitz条件，单边Lipschitz条件和拟单边Lipschitz条件.

注1.1 一个单边Lipschitz函数［5］显然是一个拟单边Lipschitz函数.另外，通过文献［11］中的注2知一个Lipschitz非线性函数一定是一个拟单边 Lipschitz非线性函数.即，拟单边Lipschitz条件是单边Lipschitz条件的推广，单边Lipschitz条件是Lipschitz条件的推广.

首先给出如下假设:

假设(i) 系统(1)满足单边Lipschitz条件(2)，并且存在适当维数的矩阵K和P(P是正定矩阵)，使得下式成立

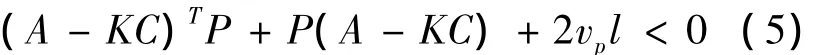
假设(ii) 系统(1)满足拟单边Lipschitz条件(4)，并且存在适当维数的矩阵K和P(P是正定矩阵)，且下面的不等式成立

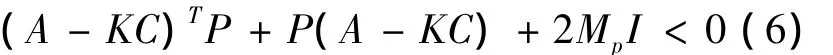
尽管拟单边Lipschitz常数矩阵在非线性系统观测器设计上更优于单边Lipschitz常数和Lipschitz常数，但很难获得(4-5)的正定解P［13］，原因有两个:(Ⅰ)很难去计算(4)(5)中的Mp.(Ⅱ)即使可以从中计算出来Mp，但是矩阵不等式(4)(5)的可行性和可解性一样是很难讨论，因为 Mp要依赖于正定解 P.即不等式(4)(5)并不是LMIS.因此研究其可行性和可解性就变得尤为重要.

2 文献的结论

考虑系统(1)的如下形式的观测器

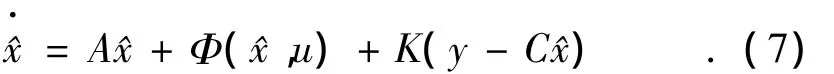
则误差系统为

下面先介绍几个引理［5，6，11］.

引理2.1［6］如果假设(ii)成立，则(7)为系统(1)的渐进稳定估计.

引理2.2［12］假定(4)的正定解P有分块矩阵表示形式

其中 P1∈ Rp×p，P2∈ Rp×(n-p)，P3∈ R(n-p)×(n-p).如果C=(IpO)并且条件(i)成立，则带有单边Lipschitz条件(2)的非线性系统(1)有一个如下形式的降维观测器:

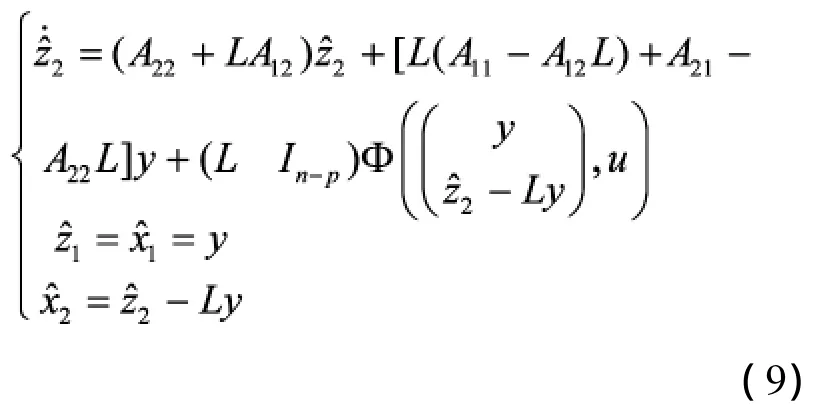
下面的引理指出假定C有形式(IpO)并不是至关重要的.

引理2.3［12］对于带有单边Lipschitz条件(2)的系统(1)，如果C是行满秩的且可以选择一个增益阵K，使得下列不等式

有一个正定对称解P，则系统(1)有由(7)给出的全维观测器，以及如下的降维观测器:

其中

3 主要结论

在这一节，将提出非线性系统(1)在几种重要情况下观测器存在性的充分条件.给出的结论至少是已有文献的补充，并且较之已有条件要减少保守性.结论表明对于大量的非线性系统观测器的设计来说，拟单边Lipschitz常数矩阵要优于单边Lipschitz常数和Lipschitz常数.首先，类似引理2.2和引理2.3，我们给出下面重要的定理

定理3.1 (1)如果C=(IpO)，并且条件(ii)成立，那么带有拟单边Lipschitz条件(3)的非线性系统(1)具有一个全维观测器(7)及降维观测器(9).

(2)如果C是行满秩的，并且条件(ii)成立，那么带有拟单边Lipschitz条件(9)的非线性系统(1)有一个全维观测器(7)及降维观测器(10).

其证明完全类似于引理2.2.和引理2.3，在此省略.

注3.1 如果C=(IpO)，对于满足条件(3)的系统(1)来说，如果只考虑降维观测器，那么拟单边Lipschitz条件(3)可以减弱为

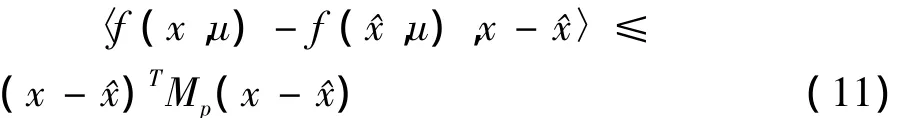
现在我们研究不等式(4)和(5)的可行解.通过注1.1知不等式(5)是不等式(4)的延伸，所以只需研究不等式(5)的可行解即可.

下面对于特定结构的Φ(x，u)研究如何将矩阵不等式(5)变换为一个线性矩阵不等式(LMI).

3.1 假定

其中fi(x，u)(i=1，2，…，n)是带有Lipschitz常数γi的 非线性Lipschitz函数.

定理3.2 考虑系统(1)带有假定条件(2).如果存在正实数 m1，m2，…，mn和增益矩阵K使得下列LMI:

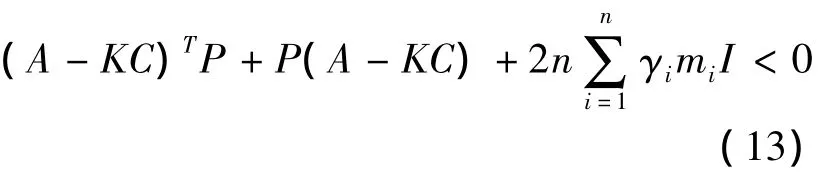
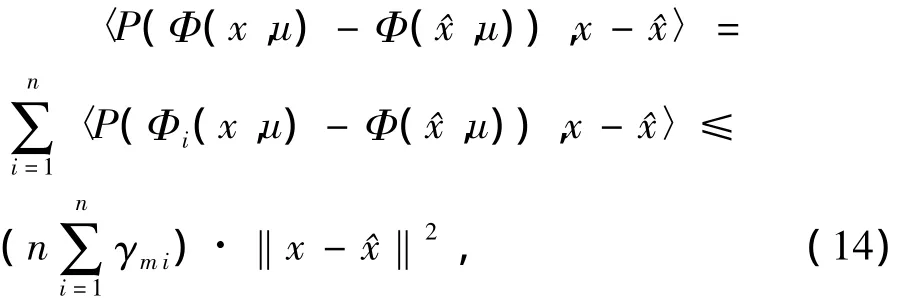
注3.2 如果只考虑降维观测器设计，则由(14)式及注3.1的(11)式可知是PΦ的拟单边Lipschitz常数矩阵，且可以通过m1，m2，…，mn来适当的调整和的值.

3.2 在上一种情形中

LMI(13)给出了一类非线性系统观测器存在性的充分条件.然而它需要(13)式的正定解P下面我们考虑不等式(5)的正定解可以是任意结构的情况.

假设系统(1)的非线性部分Φ有以下结构:

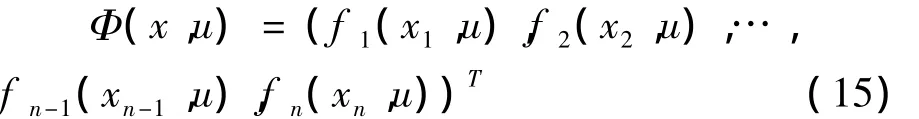
其中fi(xi，u)(i=1，2，…，n)单调递增且关于xi可微，且满足，则有定理3.3.考虑系统(1)的非线性系统部分满足如上假设，如果存在增益矩阵K使得下列LMI:

有正定解P，其中，

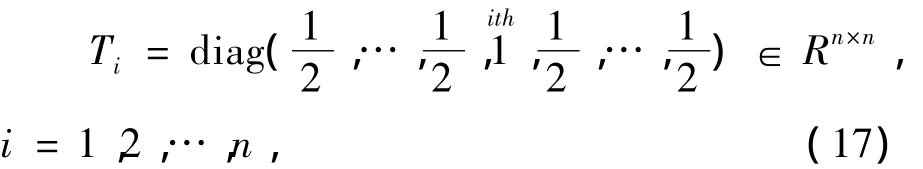
则非线性系统(1)具有(7)形式的全维观测器及(11)形式的降维观测器(当C=(IpO)时为(9)).

证明 根据定理3.1知只需证对于任意的正定矩阵P，Mp=是 PΦ 的拟单边Lipschitz常数矩阵.下面分情形由特殊到一般给予证明:

对于任意正定矩阵 P=(pij)n×n× Rn×n，令

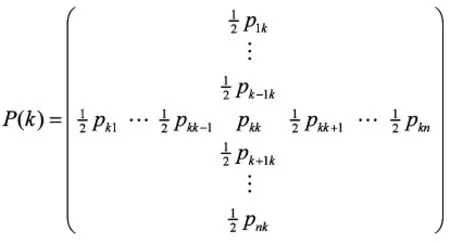
该矩阵表示中空白的部分为0元素，非空白部分的元素在第k行k列.显然TkPTk＞0，且可推得TkPTk＞P(k).因此，对于任意的正定矩阵P∈Rn×n，由中值定理知存在 ξ∈ Co(xk，)使得

因此，Mp=γkTkPTk是PΦ的拟单边Lipschitz常数矩阵.

对于一般情形我们可以将Φ(x，u)写成如下形式:

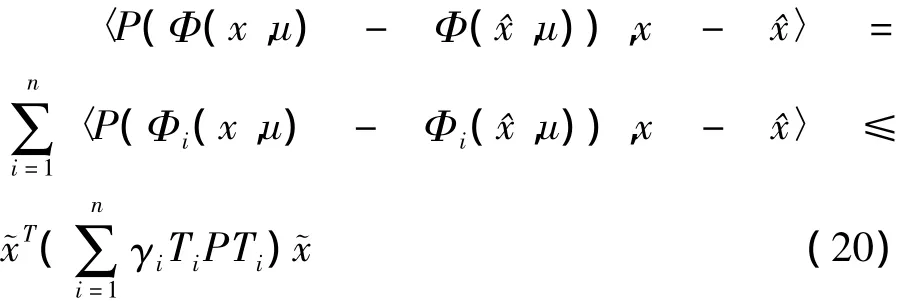
3.3 第三种情形可由下述定理直接阐述

定理3.4 如果非线性系统(1)满足下列条件:

有一个正定解P，那么(9)是系统(1)的降维观测器.

证明 依据向量值函数中值定理，对于任意的正定矩阵P=(pij)m×n∈Rm×n及x-^x=(0，0，…，xn-^x)T∈ Rn，存在 ξ∈ Co(x，^x)使得

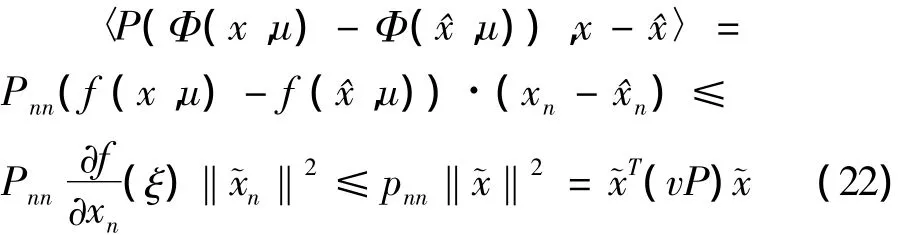
因此，Φ(x，u)满足注3.1中的不等式(10)，其中Mp=vP.依据定理3.1和注3.1知，(9)是系统(1)的降维观测器.

4 数值算例

在这一章，将通过数值算例来验证本文所给结论的有效性.

例 考虑在文献［7］中研究的三角Lipschitz非线性系统:

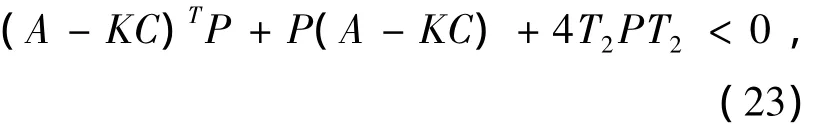
图1 x的仿真结果

初始条件为 x(0)=(0.5，1)'，^x(0)=(4，6)'.

下面考虑该系统的降维观测器，我们可以利用定理3.8，解LMI(3.13)即

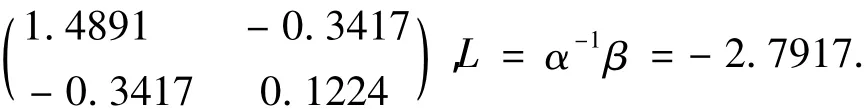
从降维观测器(9)，我们得到x2的状态仿真图2，其中初始条件为x2(0)=1，^x2(0)=4.4.

5 结束语

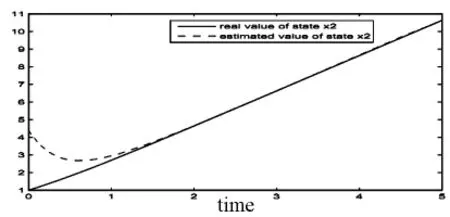
图2 x的状态仿真

拟单边Lipschitz条件是对单边Lipschitz条件的推广，单边Lipschitz条件是Lipschitz条件的推广.论文表明对于大量非线性系统的观测器设计而言，拟单边Lipschitz常数矩阵要优于单边Lipschitz常数和Lipschitz常数.我们希望mp可以尽可能多的利用非线性部分所提供的信息进行观测器设计，但这样的mp是很难找到的，并且解不等式(5)也存在困难，原因是不等式(5)并非直接就是LMI.本文研究了不等式(5)的可行性和可解性.对几种重要的情况加以讨论，获得了使不等式(5)成为LMI的的拟单边Lipschitz常数矩阵mp.需要指出的是所给结论不仅可以直接应用于一些重要的Lipschitz非线性系统，同时对一些非传统意义的Lipschitz非线性系统(只需是拟单边Lipschitz非线性系统)也同样适用，所提出的方法是对文献［11，12］中相关理论的补充.最后给出仿真算例对结论加以验证.

［1］ Besancon G，Hammouri H.On uniform oberservationnonuniformly observable systems，Syst.Control Lett.，1996，29:9-19.

［2］ Besancon G，Hammouri H.Reduced order observer for a classof nonuni-formly observable systems，in Proc.34th Conf.Decision and Control，New Orleans，L A，1995:121-125.

［3］ Dawson D M.On the state observation and output feedbackproblems for nonlinear uncertain dynamic systems，Syst.ControlLett，1992，18:217-222.

［4］ Dekker K，Verwer J G.Stability of Runge-Kutta methods for Stiff Nonlinear Differential Equations.Amsterdam:North-Holland.

［5］ Guangda H，2006，Observers for one-sided Lipschitz nonlinear Systems.IMA J.Math.Control Inf，1984，23:395-401.

［6］ Guangda H.A note on observer for one-sided Lipschitz non-linear Systems.IMA J.Math.Control inf，2008，25:297-303.

［7］ Gauthier J P.Hammouri H，Othman S.A simple observer fornonlinear system.Applications to bioreactors，IEEE Tran.Automat.Contro.，1992，37(6)，875-880.

［8］ Ibrir S.Circle-criterion approach to discrete-time nonlinear observer design，Automatica，2007，43，1432-1441.

［9］ Kazantzis N，Kravaris C.Nonlinear observers design using Lyapunoov’s auxiliary theorem，Systems and Control Letters，1998，34:241-247.

［10］ Khalil H K，Esfandiari F.Semiglobal stabilization of a class of nonlinear systems using output feedback，IEEE Trans.Automat.Contr，1993，38:1412-1415.

［11］ Mingyue X，Guang da H，Yan bin.Reduced-order observer design for one-sided Lipschitz non-linear systems.IMA J Math Control Inf，2009，26(2):299-311.

［12］ Zhu F，Han.Anote on observer for Lipschitz nonlinear systems.IEEE Trans，Autom Control，2002，47(2):1751-1754.