K4-minor-free图的邻点可区别全染色
2012-10-23史小艺张宁万慧敏
史小艺,张宁,万慧敏
(中国矿业大学 理学院,江苏 徐州 221008)
K4-minor-free图的邻点可区别全染色
史小艺,张宁,万慧敏
(中国矿业大学 理学院,江苏 徐州 221008)
图G的一个正常全染色被称为邻点可区别全染色,如果G中任意两个相邻点的色集合不同.论文确定了 k4-minor-free图的邻点可区别全色数.
全染色;邻点可区别全染色;邻点可区别全色数; k4-minor-free图
本文所考虑的图均为连通、有限、无向的简单图. V( G)和 E( G)分别表示图G的顶点集和边集,δ( G)和Δ (G)分别表示G中顶点的最小度和最大度.设u ∈ V,在图G中与u相邻的点的全体的个数称为u的度数,记为 d( u).把 d( u )= k的点叫做k-点,类似地,把 d( u )> k的点叫做k+-点,d ( u )<k的点叫做k--点,度为1的点被称为叶子.如果一个图H能从另一个图G的子图通过一些列的边收缩而得到,则称H是G的一个minor(图子式);如果H不是G的图子式则称G是H-minor-free的.
定义[1]574对阶数不小于2的连通图 G( V, E),令f为 V( G )∪E( G )→{1, 2,… ,k }的映射,其中k为正整数,对任意的 u∈ V( G),记 C( u )= {f ( u )}∪ {f( uv) uv ∈E( G)},如果 f满足下列条件:
1)对任意的 uv, vw ∈ E( G),u ≠ w,有 f( uv )≠ f( vw);
2)对任意的 uv∈ E( G),若 f( u )≠ f( v)、 f( u )≠ f( uv)、 f( v) ≠ f( uv),则f为图G的一个k-正常全染色,最小的k值为图G的全色数,记为 χt(G).进一步,如果f还满足:
3)对任意 uv ∈ E( G),u ≠ v,有 C( u )≠ C( v),则称f为图G的一个k-邻点可区别全染色,简记为k-AVDTC,且称 χat(G )= min {k G的 k -AVDTC}为图G的邻点可区别全色数.
Behzad[2]和Vizing[3]分别独立地提出了有关图的全染色猜想.
猜想1 对任意的简单图G, χt(G )≤ Δ (G)+2.
2004年张忠辅等[1]首次提出了邻点可区别全染色的概念,证明了完全图、完全二部图、圈、扇、轮和树等简单图的邻点可区别全色数,并根据这些结论,对照全染色猜想提出了猜想2.
猜想2 对阶数不小于2的简单连通图G,有 χat(G )≤ Δ (G)+3.
文献[4-5]分别独立证明了对于 Δ (G)= 3的图猜想2成立.
引理1[1]575若G是一个图,则 χat(G)≥ Δ+1;当G有两个相邻的最大度点时,χat(G )≥ Δ+2.
引理2[4-5]若 Δ (G)= 3,则 χat(G)≤6.
文献[6-9]研究了2-连通外平面图的邻点可区别全色数,文献[10]证明了外平面图中猜想2成立.本文主要讨论 k4-minor-free图的邻点可区别全染色,并证明:若G是一个 Δ (G)≥ 5的 k4-minor-free图,则Δ (G )+ 1≤ χat(G)≤Δ (G)+2,且 χat(G )=Δ (G)+ 2当且仅当G包含相邻的最大度点.
图G是外平面的当且仅当G是 k4-minor-free和 k2,3-minor-free的,因此 k4-minor-free图是包含外平面图在内的一类特殊平面图.本文的主要定理推广了文献[10]中的结论.
引理3[11]每一个 Δ (G)≥ 3的连通 k4-minor-free图G必含有 C1到 C5这5个子图之一.
415
C1:一个顶点v相邻于至少一个叶子和至多两个3+-点.
C2:一条路x1x2…xm,m ≥4,满足 d( x1)≥ 3, d( xm)≥ 2, d( xi)=2,i = 2,3,… ,m -1.
C3:一个3-圈xyzx使得 d( x)=2, 2≤ d( y)≤3, d( z)≥ 3.
C4:两个3-圈 xx1zx和 yy1zy使得 d( z)= 4, d( x1)= d( y1)= 2.
C5:一个4-圈 y1y2y3y4y1使得 d( y2)= d( y4)= 2, d (y1),d (y3)≥ 3,并且 y1至多与两个3+-点相邻.
2 主要结果
定理1 若G是一个 Δ (G)≥ 4的 k4-minor-free图,则 χat(G )≤ Δ (G)+2.
1) C1:存在一个k-点v相邻于 v1, v2,… ,vk,使得 d( v1)=1, d( vi)≤ 2( i=2,3,… ,k -2).
令H = G - v1,由归纳假设,H有一个应用颜色集合 C= {1,2,…,Δ (G)+2}的 (Δ ( G)+ 2)-邻点可区别全染色f.不失一般性,假设 f( v)=1, f( vvi)=i( i= 2,3,… ,k ).显然 Δ (G )≥ d( v )=k.证明又分以下3种子情况:
① k=2.若 d( v2)≠ 2,用3染 vv1.若 d( v2)= 2,如果存在 c∈ {3, 4,5}使得 c ∉ Cf(v2),给 vv1染c,给v1染集合 C {f( v ),f( vv1)}中的颜色.
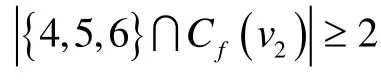
2) C2:存在一条路 x1x2…xm,m ≥4,满足 d( x1)≥ 3, d( xm)≥ 2, d( xi)= 2( i= 2,3,… ,m -1).
令H = G - x2x3,根据归纳假设,图H有一个应用颜色集合 C= {1,2,…,Δ (G)+2}的 (Δ ( G)+2)-邻点可区别全染色f.若 d( x4)≠2,给 x2染或改染颜色 a ∈C {f(x1x2),f(x3x4),f( x1),f( x3),}且在集合C {f( x3),f( x1x2),f( x3x4),a} 中任选一种颜色给 x2x3.若 d( x4)= 2,给 x3x4染或改染颜色a ∈ C{f ( x2), f( x4), f( x5),f( x4x5)},给 x3染或改染 b ∈C {a, f( x2), f( x4),f( x4x5)}且在集合C {a, b, f( x2),f( x1x2)}中任选一种颜色给 x2x3.
3) C3:一个3-圈xyzx使得 d( x)=2, 2≤ d( y)≤3.
令H = G - xy,由归纳假设,H有一个应用颜色集合 C= {1,2,…,Δ (G)+2}的 (Δ ( G)+ 2)-邻点可区别全染色 f.证明又分为以下3种子情况:
① d( y)=2.给xy染色集合 C {f( x ),f(y ),f( xz) ,f(yz )}中的颜色,给x染或改染集合C {f(y ),f( z) ,f( xy ),f( xz) }中的颜色.
② d( y)= 3.令u ≠ x,z是y的第3个邻点. 1a d( z)≥ 4.i)若 d( u)≠3,给xy染集合 C {f(x) ,f(y ),f(xz) ,f(yz) ,f(yu )}中的颜色.ii)若d( u)= 3,令u1, u2≠ y是u的另两个邻点.若给xy正常染色即可.否则,给y改染一个颜色 a∈C (Cf(u )∪ {f ( z )}),然后对xy正常染色即可.因为
4) C4:存在两个3-圈 xx1zx和 yy1zy使得 d( z)=4, d( x1)= d( y1)= 2.
根据情况3),可以假设 d( x)≥ 4、 d( y)≥4,令 H = G - zx1,由归纳假设,H有一个应用颜色集合C= {1,2,…,Δ (G)+2}的 (Δ ( G)+ 2)-邻点可区别全染色f,证明又分为以下2种子情况:
① d( x),d( y)≥5.给 zx1染集合 C {f( xz) ,f(yz) ,f( xx1),f( zy1),f( x1),f( z) }中的颜色.
② 假设 d( x)= 4,令 u1, u2≠ x1,z是x的另外两个邻点,不妨设 f( x)=1、 f( xu1)= 2、 f( xu2)= 3、f( xz)=4、 f( xx1)= 5,6 ∉ Cf(x ).若d( y)≥5,如果 6 ∉{f( z) ,f( zy ),f( zy1)},给 zx1染6,给 x1染或改染集合 C {f( x ),f( z) , f( xx1),f( x1z )}中的颜色.否则,给 zx1正常染色即可.若 d( y)= 4,因为Cf(y)=5且C≥6,存在一个颜色 a ∈C Cf(y ),当 a≥ 6,若 a ∉ Cf(z),给 zx1染a, x1染或改染C { f( xx1),f( zx1),f( x ),f( z) }中的颜色,否则,给 zx1正常染色;当1 ≤ a≤ 5,i)a ∈ Cf(z),若 6 ∉ Cf(z),给 zx1染6,x1染或改染 C {f( xx1),f( zx1),f( x),f( z) }中的颜色,若 6 ∈ Cf(z),只需对 zx1正常染色.ii)a∉ Cf(z),给y1z改染颜色a,y1染或改染集合 C {f(y ),f( z) , f(yy1),f(y1z) }中的颜色,随后证明与前面情况相同.
5) C5:一个4-圈 y1y2y3y4y1使得 d(y2)= d(y4)= 2,d( y1),d( y3)≥ 3,并且 y1至多与两个3+-点相邻.
令 u1, u2,… ,um是 y1不同于 y2和 y4的邻点,如果 m≥ 3,进一步假设对于任意 i= 1,2,… ,m -2有d( ui)≤2.不失一般性,假设 d( y1)= d( um-1)= d( um),否则结论很容易证出.令 H = G - y1y2,根据归纳假设,H有一个应用颜色集合 C= {1,2,…,Δ (G)+2}的 (Δ ( G)+ 2)-邻点可区别全染色f.不失一般性,假设 f(y1)=1、f(y1y4)= 2、 f(y1ui)= i+2( i= 1,2,… ,m ).因C =Δ (G)+2,d( y1)=m+2≤Δ (G),可以看出 m+ 3,m +4∈C .
① 若 存 在 c∈{m +3,m +4}使 得 c∈ Cf(um-1)∩ Cf(um), 给y1y2染 a∈{m +3,m + 4}{c}.当f(y2y3)= a时,需交换 y2y3和 y3y4的颜色,因为 f(y2y3)≠ f(y3y4)和 a≠ 1,2,给 y2染或改染集合C { f(y2y3), f(y3y4), f(y3),1,a}中的颜色;当 f(y2)= a时,给 y2染或改染集合 C {1,a,f(y2y3),f(y3)}中的颜色.
② 若 {m +3,m +4} ⊆ Cf(um-1)Cf(um)或 {m + 3,m +4} ∈ Cf(um)Cf(um-1), 给y1y2染 集 合{m + 3,m + 4}f(y2y3)中的颜色,给y2染或改染 C {1,a, f(y2y3),f(y3)}中的颜色.
③ 若存在 c∈{m +3,m +4}使得 c∉ Cf(um-1)∪ Cf(um),给y1y2染c,当 f(y2y3)= c或 f(y2)= c时,证明与①相同.
④ 假设 m +3∈ Cf(um-1)Cf(um)和 m +4∈ Cf(um)Cf(um-1),给y1y4染 a∈{m +3,m + 4}{f(y3y4)},给y1y2染 b∈ {m + 3,m + 4}{a},给y2染或改染集合 C {1,b, f(y2y3),f(y3)}中的颜色,给 y4染或改染集合C {1,a, f(y3y4),f(y3)}中的颜色.
定理2 若G是一个 Δ (G)≥ 5且没有相邻最大度点的 k4-minor-free图,则 χat(G )≤ Δ (G)+1.
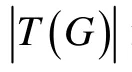
若G含有 C1.令 H = G - v1,H有一个应用颜色集合 C= {1,2,…,Δ (G)+1}的 (Δ ( G)+ 1)-邻点可区别全染色f.如果 k = d( v )<Δ (G),那么C=Δ (G)+1 ≥ k+ 2,证明类似于定理1中的 C1.如果k = d( v )=Δ (G),那么 d( vi)< Δ (G)( i = k - 1,k),根据假设,只需对 vv1正常染色,给 v1染集合C {f( v ),f( vv1)}中的颜色.
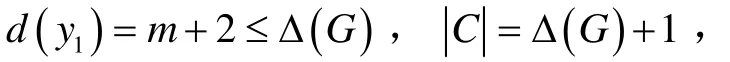
由定理1和定理2,立即推出下面的结论:
定理3 若G是一个 Δ (G)≥ 5的k4-minor-free图,则 Δ (G)+ 1≤ χat(G)≤ Δ (G )+2,且 χat(G)= Δ (G)+ 2当且仅当G包含相邻的最大度点.
[1]张忠辅,陈祥恩,李敬文,等.关于图的邻点可区别全染色[J].中国科学:A辑,2004,34(5):514-583.
[2]BEHZAD M.Graphs and their chromatic numbers[D].New York:Michigan State University,1965.
[3]VIZING V G.Some unsolved problems in graph theory[J].Uspekhi Mat Nauk,1968,23:117-134.
[4]CHEN Xiangen.On the adjacent vertex distinguishing total coloring numbers of graphs with Δ=3[J].Discrete Math,2008,308(17):4003-4007.
[5]WANG Haiying.On the adjacent vertex distinguishing total chromatic number of the graph with Δ(G)=3[J].J Comb Optim,2007,14:87-109.
[6]张少君,陈祥恩,刘信生.关于Δ(G)=5的2-连通外平面图的邻点可区别全色数[J].西北师范大学:自然科学版,2005,41(5):8-18.
[7]安明强.关于 ()6GΔ = 的2-连通外平面图的邻点可区别全色数[J].河西学院学报,2005,21(5):25-29.
[8]CHEN Xiangen,ZHANG Zhongfu.Adjacent-vertex-distinguishing total chromatic number on 2-connected outerplane graph with Δ(G)≤4[J].Journal of Lanzhou University:Natural Science,2006,42(6):96-102.
[9]朱俊俏,卜月华.2-连通外平面图的邻点可区别全染色[J].浙江师范大学学报,2009,32(1):33-39.
[10]WANG Yiqiao,WANG Weifan.Adjacent vertex distinguishing total colorings of outerplanar graphs[J].J Comb Optim,2010,19:123-133.
[11]WANG Yiqiao,WANG Weifan.Adjacent vertex distinguishing edge colorings of4k -minor-free graphs[J]. Applied Math Letters,2011,24:2034-2037.
Adjacent Vertex Distinguishing Total Coloring of4k-minor-free Graphs
SHI Xiao-yi,ZHANG Ning,WAN Hui-min
(College of Science,China University of Mining&Technology,Xuzhou 221008,China)
A proper total coloring of graphG is called adjacent vertex distinguishing if the color sets of every two adjacent vertices are different.The paper determines the adjacent vertex distinguishing total chromatic numbers of4k-minor-free graphs.
total coloring;adjacent vertex distinguishing total coloring;adjacent vertex distinguishing total chromatic number;4k-minor-free graphs
1006-7302(2012)04-0009-05
O157.5
A
2012-03-29
中央高校基本科研业务费专项基金资助项目(2010LKSX06)
史小艺(1986—),女,江苏沛县人,在读硕士生,研究方向为图论及其应用.
熊玉涛]
