基于暂态磁场梯度信号的脉冲涡流无损检测和定量评估技术

齐 勇，李 勇，陈振茂，肖美华

（1.西安交通大学 航天航空学院 机械结构强度与振动国家重点实验室，西安 710049；2.中国人民解放军94354部队，济宁 272400）

脉冲涡流检测技术（Pulsed Eddy Current Testing，简称PECT）［1－3］是一种基于传统多频／扫频涡流检测技术的新兴电磁无损检测技术。脉冲涡流检测技术采用方波信号作为激励，由于方波激励信号可等效为不同频率正弦波的叠加，因此脉冲涡流检测信号具有丰富的频谱信息，有利于深层缺陷的检测，该技术已应用于核电设备、石油／化工管道、飞机机翼等多层金属结构的电磁无损检测中。目前，脉冲涡流检测是一种对多层金属结构实现有效检测和定量评估的无损检测方法之一，该技术多采用磁场测量技术，如利用固态磁场传感器拾取暂态磁场信号。Li等人在建立脉冲涡流检测解析模型的基础上，实现了基于霍尔传感器的脉冲涡流检测探头，探究了脉冲涡流检测磁场信号在多层金属结构检测评估中的应用［4］；Tian等人采用巨磁阻传感器（GMR），实现了基于磁场信号的脉冲涡流检测技术及其对多层金属结构缺陷的检测与分类识别［5］。

磁场梯度测量技术［6］是一种测量磁场扰动大小的有效方法，广泛应用于医学核磁共振成像（MRI），具有对微观磁场变化拾取灵敏度高等优势［7］。文章将磁场梯度测量技术与脉冲涡流检测技术相结合，以实现对多层板亚表面材质劣化检测灵敏度的提高。通过仿真和试验，探究了基于暂态磁场梯度信号的脉冲涡流无损检测技术在多层板亚表面材质劣化检测中的优势性。

1 脉冲涡流检测磁场梯度信号的理论表达式

如图1（a）所示，一个由盘式线圈与固态磁场传感器（如霍尔元件、巨磁阻传感器、磁通门等）构成的脉冲涡流检测探头放置于多层金属结构上方。

假设图1（a）所建立的脉冲涡流检测模型中，多层金属结构各层材料为线性、均匀且各向同性的静止媒质。基于ETREE解析法［8］，线圈激发磁场（）和涡流激发磁场（）的z分量磁场信号理论解析式为［9－10］：

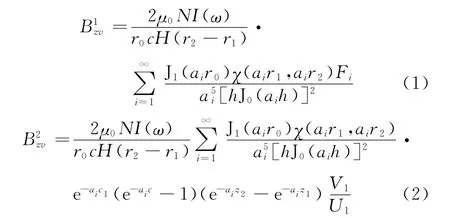
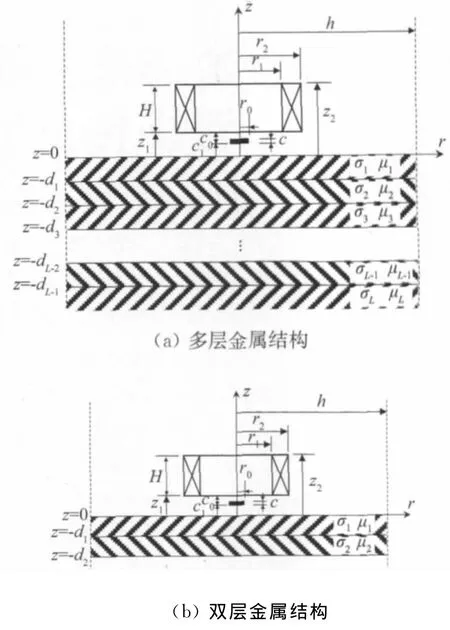
图1 多层金属结构脉冲涡流检测模型示意图

式（1）和（2）中ω是脉冲涡流检测信号谐波角频率；μ0是真空磁导率；Jn为贝塞尔函数；I（ω）为激励电流强度；N为线圈匝数；h为涡流场边界距离；ai为J1（aih）＝0的正根；V1／U1为金属体电磁场反射系数，可由参考文献［4］中相关公式计算得到。公式中涉及的函数还包括：

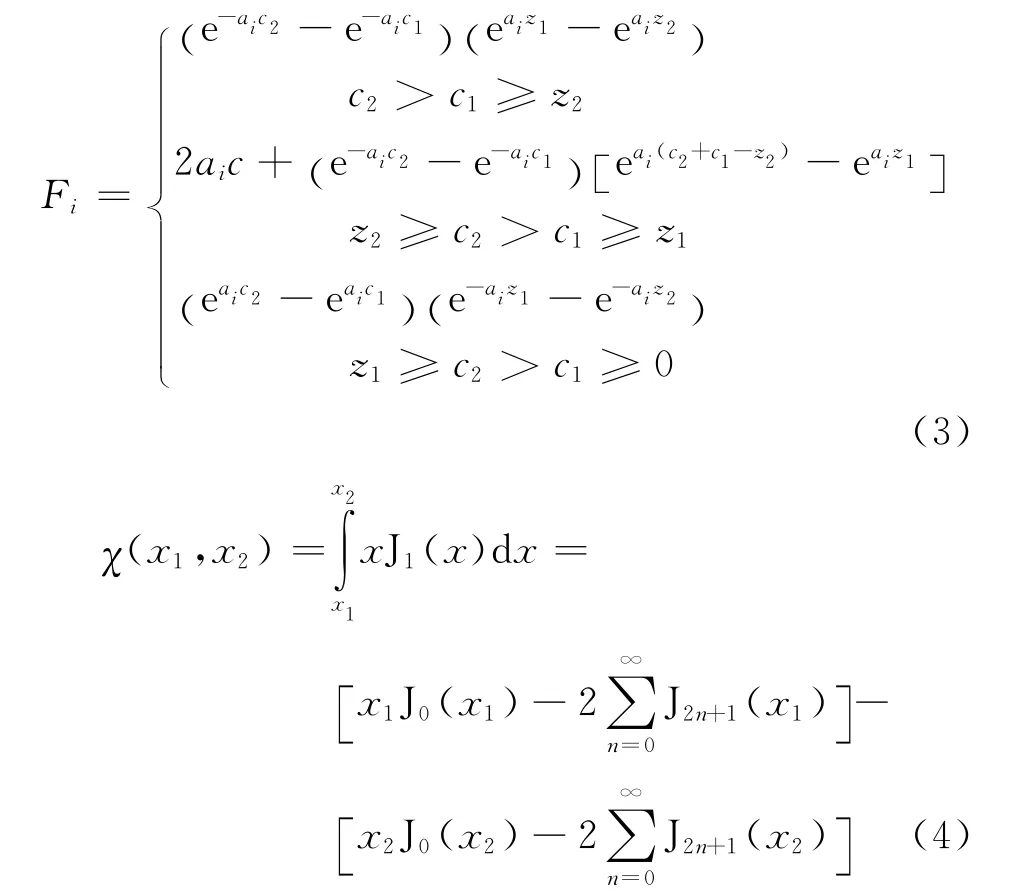
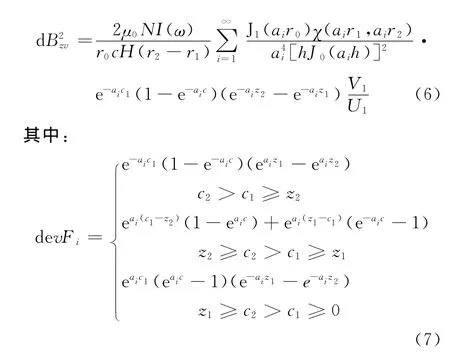
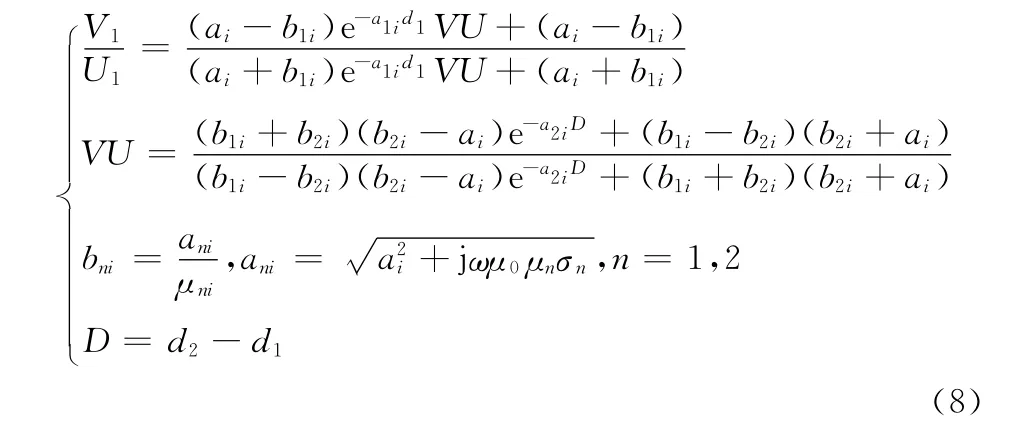
下层板导电率的变化对金属体电磁场反射系数的影响可写为：

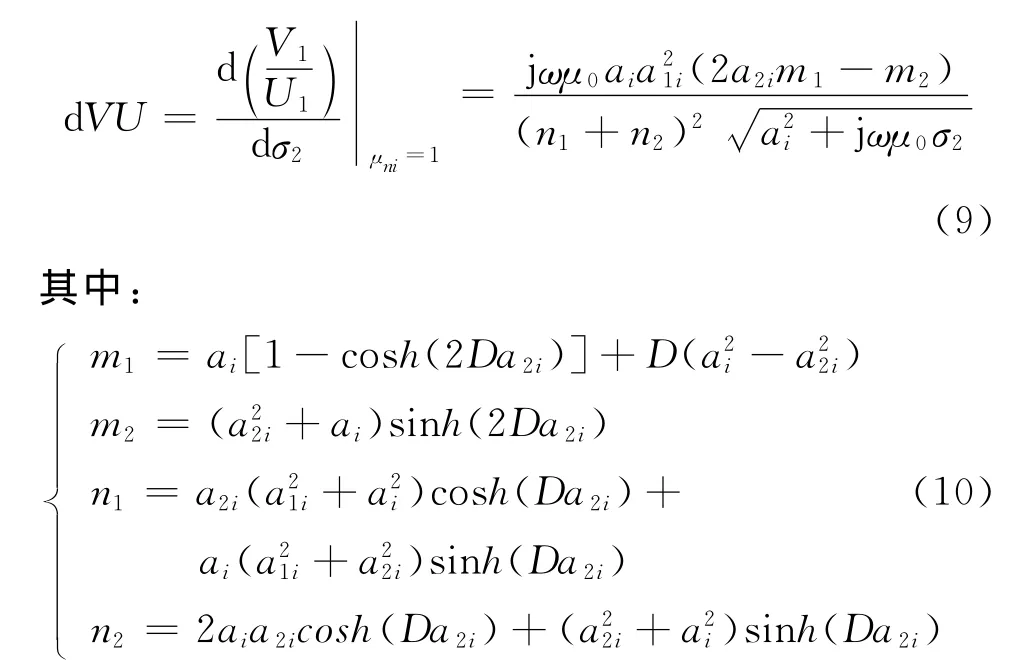
基于式（2），（6）和（9），下层板金属导电率变化对磁场梯度信号和磁场信号的影响可写为：

2 脉冲涡流检测磁场梯度信号的仿真研究

如图1（b）所示，二维轴对称脉冲涡流检测仿真模型由探头（盘式激励线圈和磁场传感器）和被测试件组成，试件为典型双层金属平板结构，上层板导电率为定值，下层板导电率变化，以模拟下层板材质劣化。因脉冲涡流信号可等效为不同频率涡流信号的叠加，故对所建立的脉冲涡流磁场梯度信号理论表达式的验证在频域中进行。仿真模型各参数为：激励线圈外半径r2＝24.64mm；激励线圈内半径r1＝22.57mm；激励线圈高度H＝6.62mm；激励线圈匝数N＝804；探头设计提离z1＝0.64mm；磁场传感器底部高度c1＝0.64mm；磁场传感器厚度c＝0.46mm；上层金属板导电率σ1＝34MS·m－1；下层金属板导电率σ2＝10～59.98MS·m－1；上／下层金属板相对磁导率μ1r／μ2r＝1；上层金属板厚度d1＝1.50mm；下层金属板厚度d2－d1＝8mm；激励电流频率f＝10～10000Hz；激励电流幅值I＝0.50A；磁场传感器半径r0＝0.91mm。

同时采用 FEM－BEM［11］法和 ETREE法求取图1（b）模型磁场梯度信号，图2为下层金属板导电率分别10，40和60MS／m时，磁场梯度信号实部和虚部与激励频率关系曲线。图3为激励频率分别为100，1，10kHz时，磁场梯度信号实部（图3（a）），虚部（图3（b））对下层金属板导电率变化的响应。由图2和图3可见，ETREE和FEM－BEM两种方法计算结果基本吻合。通过进一步数据分析，发现计算结果相对误差在1%以内，从而验证了所建立的磁场梯度信号（式（6））及其对下层金属板导电率变化响应解析式（式（11））的正确性。然而，由于采用ETREE法求解信号无需对求解域进行网格剖分，能在1s内得到计算结果，故较FEM－BEM法计算效率更高。

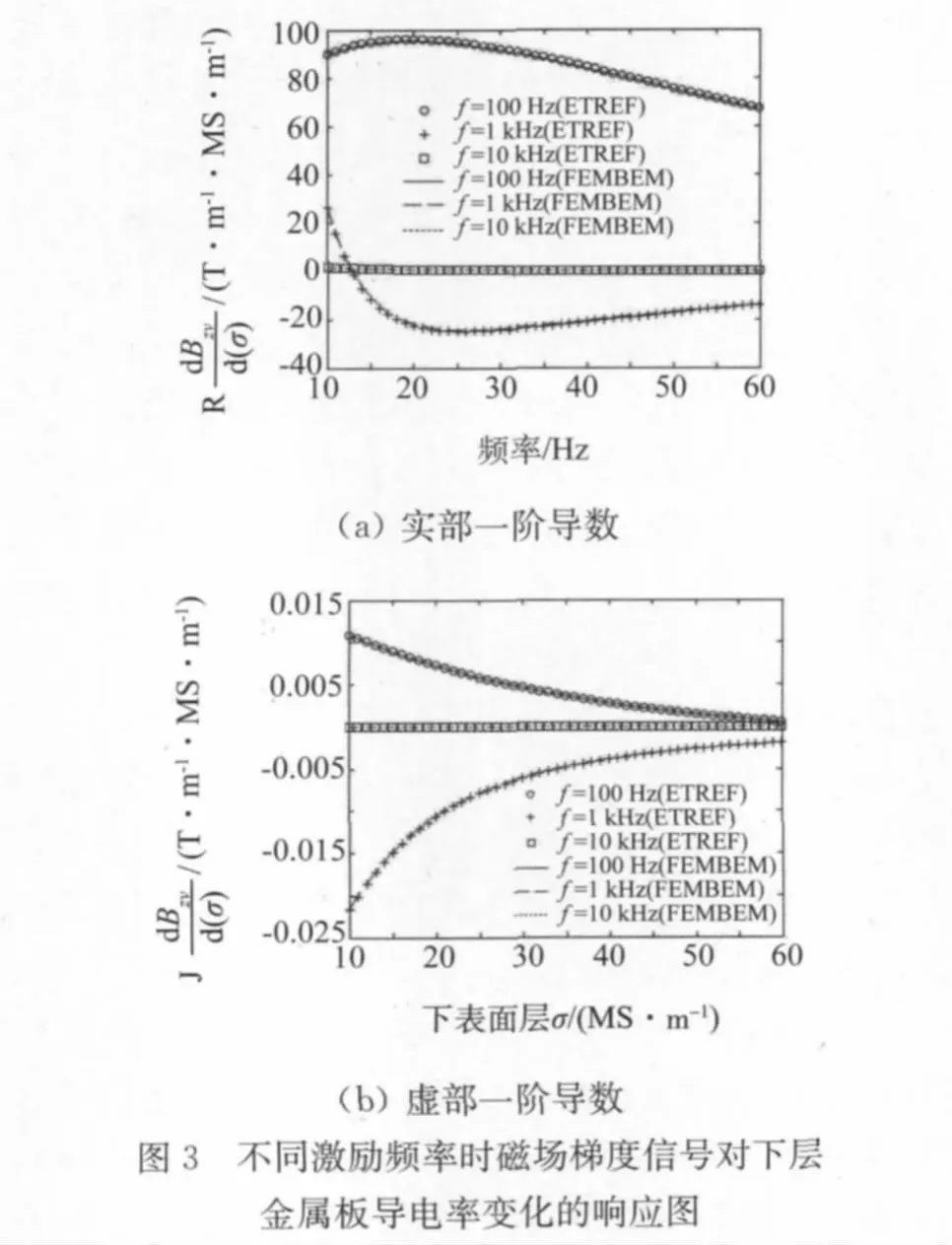
图4为磁场梯度信号和磁场信号实部、虚部对下层金属板导电率变化响应曲线。由图4可见，与磁场信号相比，磁场梯度信号对下层金属板导电率变化反应更为灵敏，可提升近两个数量级，体现了磁场梯度信号在金属部件亚表面层材质劣化定量评估中的优势。

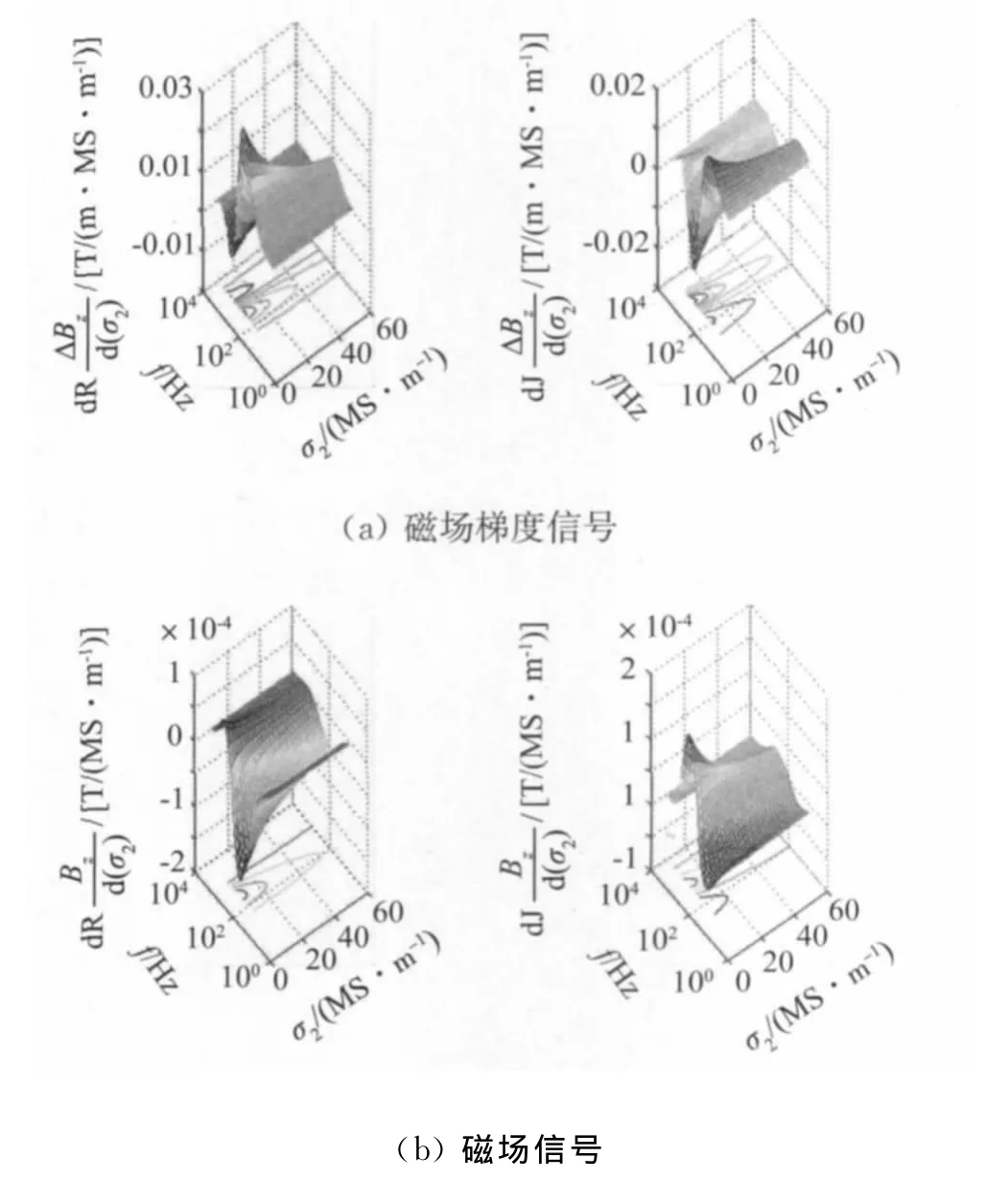
图4 磁场梯度信号和磁场信号实部，虚部对下层金属板导电率变化灵敏度曲线

3 脉冲涡流检测磁场梯度信号试验

脉冲涡流试验平台及其系统框图如图5所示。试验中，为比较磁场信号和磁场梯度信号对亚表面层导电率变化的灵敏度，分别制作了两类脉冲涡流检测探头，各探头均由激励线圈和固态磁场传感器组成。激励线圈参数为：外径23mm，内径20mm，线圈高20mm，匝数210，线径0.27mm。检测探头分别采用两类巨磁阻传感器（均置于激励线圈底部中心位置）：① NVE GMR－AA004－02测量总磁场z分量信号。② NVE GMR－ABL005测量总磁场z分量梯度信号。

图5 脉冲涡流检测试验平台及其系统框图

功率放大器输出最大幅值为5V的电压，以驱动激励线圈。鉴于NVE GMR传感器存在非线性和磁滞现象，输出的线圈驱动电压置入4V直流分量，保证两个传感器均工作在线性区域。为模拟多层金属板亚表面材质劣化，选用典型双层金属板结构，上层金属板尺寸为60mm×60mm×1.5mm，材质为黄铜（导电率为14MS／m）；下层金属板尺寸为60mm×60mm×3mm，材质可变，分别为黄铜，钨（导电率为20MS／m）以及铝（导电率为34MS／m）。各层板材料相对磁导率均为1。

图6（a）为下层板不同导电率的磁场梯度信号，图6（b）为下层板不同导电率的磁场差分信号（参考信号为空气中探头输出的磁场信号）。需要指出的是，各试验信号与仿真计算结果相近。由图6可见，磁场梯度信号与磁场差分信号存在明显差异。磁场梯度信号幅值（绝对值）随下层板导电率的减小而减小，磁场差分信号幅值（绝对值）与下层板导电率呈递增关系。

图6 下层板不同导电率的磁场梯度信号和磁场差分信号

为证明磁场梯度信号在多层板亚表面材质劣化检测中的优势，在信号处理中，分别提取磁场梯度信号和磁场差分信号的特征，即峰值（PV）［12］，并采用拟合函数，建立PV与亚表面层电导率σ间的关联规律，进而对该拟合函数进行求导，即d（PV）／d（σ），计算结果如图7所示。可见，d（PV磁场梯度）／d（σ）数值远大于d（PV磁场差分）／d（σ），表明磁场梯度信号对第二层金属板导电率变化灵敏度较大。该结果印证了前述理论仿真结论，体现了脉冲涡流磁场梯度信号在金属部件亚表面层材质劣化定量评估中的优势。

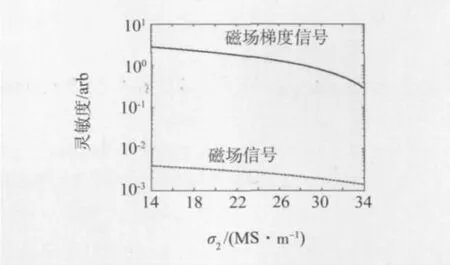
图7 磁场梯度信号和磁场信号对第二层金属板导电率变化的灵敏度对比

4 总结

基于ETREE解析法，推导了基于磁场梯度信号的脉冲涡流检测亚表面层材质劣化理论表达式，同时，通过与FEM－BEM仿真结果的对比，验证了所建立理论表达式的正确性。通过仿真和试验研究发现，与脉冲涡流磁场差分信号相比，脉冲涡流磁场梯度信号对金属部件亚表面材质劣化灵敏度较大，从而证明了基于暂态磁场梯度信号的脉冲涡流检测技术在金属部件亚表面层材质劣化定量评估中的优势。

［1］杨宾峰，罗飞路.脉冲涡流检测系统影响因素分析［J］.无损检测，2008，30（2）：104－106.

［2］张思全，陈铁群，朱佳震.脉冲涡流检测技术的进展［J］.无损检测，2008，30（11）：838－864.

［3］周德强，张斌强，田贵云，等.脉冲涡流检测中裂纹的深度定量及分类识别［J］.仪器仪表学报，2009，30（6）：1190－1194.

［4］Li Y，Tian G Y，Simm A.Fast analytical modelling for pulsed eddy current evaluation［J］.NDT＆E International，2008，41（6）：477－483.

［5］Tian G Y，Sophian A.Defect classification using a new feature for pulsed eddy current sensors［J］.NDT＆E International，2005，38（1）：77－82.

［6］Harrell J W.Effect of AC gradient field on magnetic measurements with an alternating gradient magnetometer［J］.Journal of Magnetism and Magnetic Materials，1999，205（1）：121－129.

［7］Bartusek K，Gescheidtova E，Vesely J.Magnetic resonance technique of gradient magnetic field measurement［C］.Proceedings of the 25th Annual International Conference of the IEEE Engineering in Medicine and Biology Society，Cancun，Mexico，2003：3282－3285.

［8］Li Y，Theodoulidis T，Tian G Y.Magnetic field－based eddy－current modeling for multilayered specimens［J］.IEEE Transactions on Magnetics，2007，43（11）：4010.

［9］Li Y，Chen Z M，Qi Y.Generalized analytical expressions of liftoff intersection in PEC and a liftoff－intersection－based fast inverse model［J］.IEEE Transactions on Magnetics，2011，47（10）：2931－2934.

［10］Tian G Y，Li Y，Mandache C.Study of lift－off invariance for pulsed eddy current signals［J］.IEEE Transactions on Magnetics，2009，45（1）：184－191.

［11］Zuo Y，Chen Z M.Enhancement of sizing capability of ECT for deep cracks by using split TR probes［J］.International Journal of Applied Electromagnetics and Mechanics，2010，33（3）：1157－1164.

［12］Abidin I Z，Li Y，Latif N A，et al.Advantages and applications of pulsed eddy current testing for comprehensive and reliable defect assessment［J］.NDT SPECTRA，2011（5）：227－233.