CXH660车铣复合加工中心立柱方案的有限元法优化设计*

徐连江 曾晨辉 钟 翔 胡 睿

(①云南省机械研究设计院，云南省机电一体化应用技术重点实验室，云南昆明 650031;②昆明台工精密机械有限公司，云南昆明 650600)

CXH660车铣及立卧转换复合机床是针对国内汽车、航天、军工等行业对高档数控机床的需求而研制开发的。该机床车、铣主轴采用大功率电主轴驱动，工件一次装夹调整后，能进行车削、铣削和钻削等多工序的复合加工。该机床是“产、学、研”合作而研发生产的新产品，体现了当今数控机床高效、高精和复合化的发展趋势。

立柱是车铣复合加工中心重要支承件，对整台机床的性能影响非常大。我们根据立柱的载荷情况及其使用要求，对立柱的截面形状、导轨的分布形式以及筋板结构布置等进行设计，形成了本产品的首个方案(A方案)，使用有限元分析方法获得了立柱在载荷工况下的变形位移和应力分布，并提出优化及改型意见。根据A方案分析结果，结合用户使用情况，对本产品进行了重大改型，形成了产品新方案(B方案)，又对B方案进行了全面CAE分析，验证了改型后的B方案各项特性均优于A方案。

根据B方案分析结果，在立柱的加工制造时，通过变形补偿使立柱的几何精度控制在允许的范围之内，从而保证了机床的加工精度。

1 方案设计

根据其他机床设计经验和本机床的功能要求，我们进行了方案设计并进行生产制造。

1.1 A 方案

1.1.1 方案的特点

方案如图1所示:立柱和横梁为整体形式，床身为平放布置，立柱上支承床鞍的2个导轨均布置在立柱的前侧，横梁中的加强筋为垂直和水平形式。

1.1.2 立柱的截面形状、加强筋及导轨设计

当机床支承件受弯曲和扭转载荷时，支承件的变形不但与截面面积大小有关，而且与截面形状，即与截面惯性矩有很大关系。一般来说，方形截面的抗弯刚度比圆形的大，而抗扭刚度则比圆形小。因此，如果支承件所承受弯矩大于扭矩，则截面形状以方形或矩形为佳［1］，其中，又以矩形截面的综合刚性最好，考虑设计空间我们采用矩形截面，如图2所示。

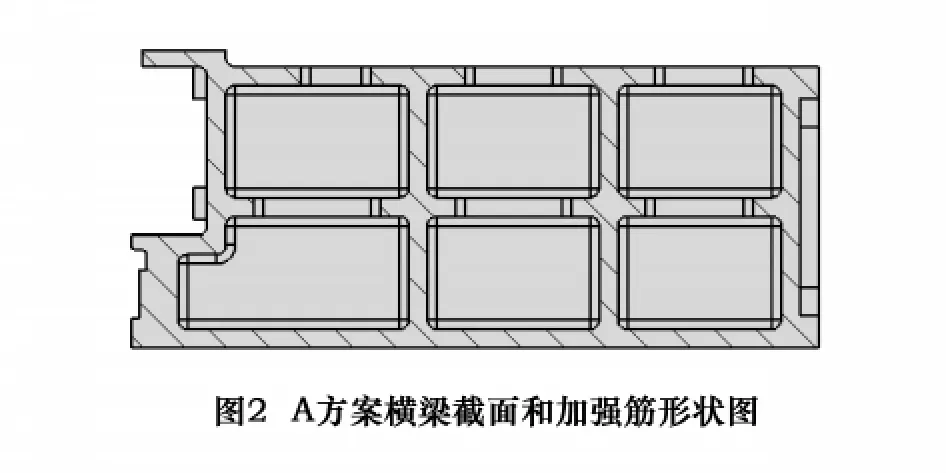
立柱的内部加强筋是根据载荷特点，通过合理布置隔板及加强筋的形式来提高立柱的整体及局部刚度。其中立柱的两侧和底部采用比较成熟的结构形式(此处不作重点论述)，重点是上横梁的结构形式，对机床的精度影响较大。方案采用横竖加强筋交叉的框架结构，这种结构具有良好的抵抗刀具切削力的特性，而且工艺简单。在横梁具体设计时，为减小横梁的弯曲变形，在加大了横梁截面高度的同时，中间分别增加了一条水平方向和两条竖直方向的隔板，与横梁两外侧墙壁一起承受下垂重力(图2)。

设计时，横梁的自重也是着重考虑的因素，若横梁自重太轻，则横梁的整体刚性无法保证;若重量设计得过重，又会加大弯曲变形，也使机床的成本增加。为了兼顾并考虑铸造的工艺性，我们通过在横、竖方向筋板的中部开设矩形窗口的方法来减轻横梁的重量，并采用大圆角过渡，以避免因应力集中而造成铸件开裂，如图2所示。

该机床采用直线滚动导轨，上下两个导轨均布置在立柱的前面(图1)。该结构简单、加工方便，但受力情况不好，相对于横梁来说系统产生的重力偏心较大，刚度不好，横梁变形较大。

用此方案试制1台后进行测试，发现变形很大，达不到预期的设计几何精度，为此我们用有限元方法对其变形和应力情况进行了理论分析。

1.1.3 A方案立柱结构的有限元分析

利用Slidworks三维软件建立横梁的实体模型，同时略去一些不影响横梁刚度的细微结构，如小孔、小倒角、小圆弧等，利用MSC－Patran软件进行前、后置处理，其中各载荷采用MPC(多点约束)方法施加，即将分析物体外的载荷刚性地施加到分析物体上，避免了大量的简化和手工运算工作，用MSC－Nastran进行分析计算。为了获得较好的计算精度，本文采用八节点四面体实体单元。

横梁材料采用铸铁HT300，材料参数为:弹性模量E=1.26×1011Pa，泊松比 μ=0.27，密度 γ=7.3×103kg/m3。

本文仅对横梁进行静态分析。

(1)立柱工况分析

据横梁的变形特点，当载荷在横梁正中间位置时，横梁的总体变形最大。为此，我们选取主轴系统在横梁中间位置时的工况进行分析，根据工况具体载荷值为横梁自重:在前置处理中直接加入“重力加速度9.8 m/s2”;滑枕—主轴系统重力:45 200 N(大小和重心位置可由Solidworks三维软件直接得出)。

分析结果如图3、图4所示。

(2)分析结论

立柱上横梁变形位移(图3)，变形量从0到0.085 mm依次增大，最大变形量为0.085 mm，出现在上横梁中间位置，机床检验精度为0.02 mm，显然是由于横梁的大变形影响了整台机床的几何精度。

应力分布图如图4所示，最大应力为36.4 MPa，远小于HT300的抗拉强度200 MPa，说明其有足够的强度，该局部应力不会对机构产生影响。

由以上分析看出问题出在立柱上横梁部分，必须对立柱上横梁进行改进。为此，我们设计了B方案。

1.2 B 方案

1.2.1 方案的特点

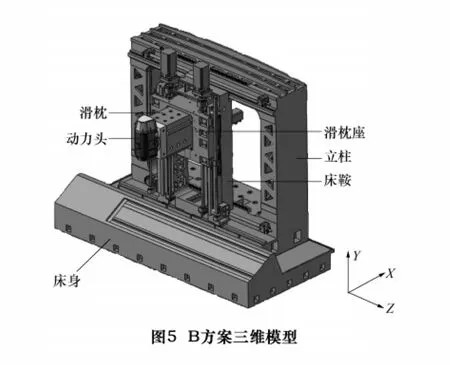
针对A方案不足，我们对其进行了重大改进，立柱和横梁依然为整体形式，但将床身设计为45°摆放位置，支承床鞍的两个导轨一个布置在立柱的前上侧，另一个导轨布置在床身上(图5)，横梁中的加强筋也做了重大改进。

1.2.2 立柱的截面形状、加强筋及导轨设计

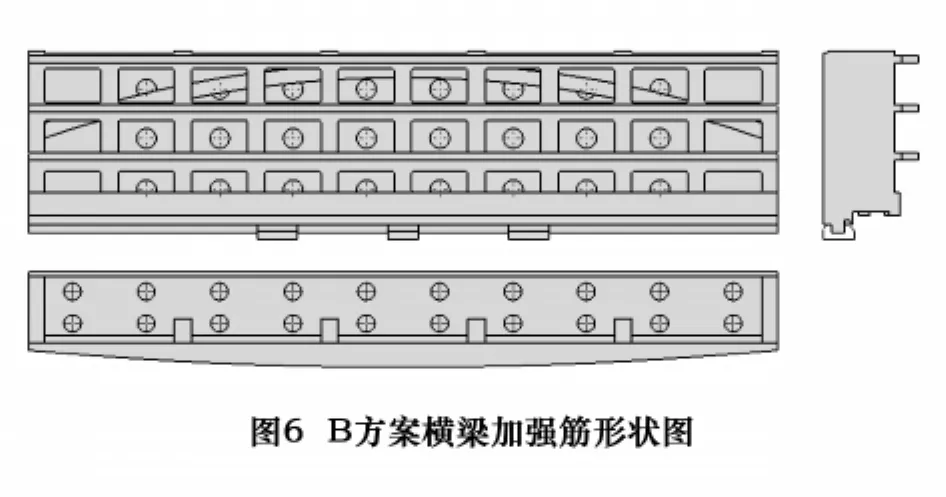
该方案中内部加强筋与A方案基本相同，但有一个重大改进，就是在原来的基础上在水平面加1个“桥拱形”加强筋，在垂直面上加3个平行“桥拱形”加强筋，这是根据“桥”的原理来设计的(图6)。

导轨的布置和A方案有重大不同，上导轨和A方案相同，但另一条导轨不是在立柱前侧，而是在床身上，如图5所示，这样大部分重力间接加在了床身上，由床鞍来承受，而不是全部由横梁来承受，减小了横梁的受力，从而间接提高了横梁的刚度。

在B方案生产制造前我们进行了有限元分析，并和A方案进行了对比。

1.2.3 B方案立柱结构的有限元分析

B方案除对横梁进行系统重力下的变形、应力分析外，还对其在切削力作用下的变形、应力进行分析。

(1)B方案工况分析

分析过程同A方案。根据工况，两种方案受力情况基本相同，具体载荷值如下:

横梁自重:在前置处理中直接加入“重力加速度9.8 m/s2”;滑枕—主轴系统重力:45 200 N(大小和重心位置可由Solidworks三维软件直接得出)。

切削力:由于切削力是在机床调试平衡后进行的，所以切削力工况需单独分析。铣削工作可以在X、Z方向进行，而两个方向的受力是不同的，故两种情况都进行分析。而车削状况受力无论在大小和方向都和Z向铣削状况［2］相同，因此无需对车削状况进行分析。

①X向铣削:由于立柱的对称性，切削力沿X轴正和负向产生的变形大小相同，方向相反，所以只取一个方向进行分析，在此取沿X负向铣削工况，根据切削参数得出受力情况为:X向+1 200 N，Y向+700 N，Z向+2 800 N(坐标方向见图5)。

②Z向铣削:取Z正向铣削，原因同上，Z向受力情况为:X向+2 800 N，Y向+700 N，Z向－1 200 N(坐标方向见图5)。

B方案分析结果见图7～12。

(2)B方案分析结论

在系统重力下立柱上横梁变形位移如图7所示，变形量从0到0.027 9 mm依次增大，最大变形量仅为0.027 9 mm，出现在上横梁中间位置，机床检验精度为0.02 mm，虽然没有达到机床的几何精度，但比较接近，通过变形补偿可以达到要求。

应力分布图如图8所示，最大应力为11.6 MPa，也小于A方案的应力，说明其有足够的强度，该局部应力不会对机构产生影响。

在两种切削力作用下变形位移如图9和11所示，两种切削方式力作用下变形位移都相对较小，其中Z向切削时变形位移相对较大，最大变形为0.015 4 mm，而机床加工精度是要求小于0.02 mm，说明加工精度可以控制在要求内。

在两种切削力作用下应力分布如图10和12所示，两种切削方式力作用下应力都相对较小，其中X向切削时应力较大，为2.96 MPa，远小于材料的抗拉强度，强度足够。

显然，经过改进的B方案比A方案有了很大的提高，按此方案能够满足机床的要求。

经以上分析，即使选择变形较小的B方案，立柱上横梁也有一定的变形，且最大变形位移出现在导轨中间位置，直接影响机床加工精度，应采取相应措施提高机床的刚度。为此我们在B方案的基础上进行了加工工艺改进，即采用数控加工方法使横梁产生倒影线形状。根据B方案分析结果，我们采用“最大倒影量”为0.028 mm，实验结果为:在Z向切削力(将产生较大变形位移)的作用下最大变形量仅为0.005 mm(机床检验精度为0.02 mm)，远远好于机床要求的精度，达到了预期的结果。

2 立柱的变形补偿

本文采用加工工艺方法，通过变形补偿来减小横梁的变形。

补偿立柱上横梁变形的常用方法是反变形法，就是使横梁导轨面的几何形状成为横梁弹性位移的倒影线，从而补偿横梁及其导轨因受自身重力及滑鞍主轴系统重力产生的弹性变形［3］。目前使横梁导轨获得横梁弹性位移倒影线形状的方法有3种:

(1)刮研导轨或数控加工获得所需的形状。

(2)在进行横梁导轨加工时，模拟其实际受力工况进行装夹，使横梁强制变形。加工后由于装夹变形作用力的释放，横梁弹性恢复成所需的形状。

(3)在横梁上安装辅助梁和加载装置，使横梁通过反向的弹性变形获得所需的形状。

对于第二种方法，由于横梁的受力情况比较复杂，因此模拟其受力条件不容易实现;而第三种安装辅助梁和加载装置可以使主轴得到较高的运动精度，但是这种方式的结构比较复杂。因此我们采用了数控加工变形补偿的方法。

通过变形补偿加工办法，很好地解决了横梁下垂以及扭转变形的问题。实际装配后，几何精度都达到了0.01 mm/1 000 mm，全长范围内不超过0.015 mm，几何精度达到了要求。

3 结语

目前企业已按B方案设计并生产了10台产品，能够很好地满足机床几何精度要求，证明B方案是非常成功的。

以往解决工程问题常采用“经典方法”，只能用来解决几何、截荷和边界条件都相对简单的结构问题，而对此类机床大型结构件的弯曲和扭转变形情况，只能将其简化后进行近似计算，其计算结果往往与实际相差较大，只能作为定性分析的参考［4］。本文以有限元软件MSC.Patran/MSC.Nastran作为主要计算工具，将有限元方法和理论应用到机床的设计中，对数控铣床的关键部件立柱的刚度和强度进行了分析计算并成功指导了产品的优化改型。对提高立柱的可靠性、精度具有重要意义，为同类零部件的结构设计提供了理论和技术指导［5］。

［1］王先逵.机械加工工艺手册［M］.2版.北京:机械工业出版社，2007.

［2］邓文英.金属工艺学(下册)［M］.3版.北京:高等教育出版社，1991.

［3］于丽菊.桥式龙门铣横梁的静动态特性研究及变形补偿［D］.大连:大连理工大学，2007.

［4］苗状.卧式车铣复合加工中心有限元分析［D］.长春:吉林大学，2009.

［5］杨曼云.XK2130大重型数控龙门铣床横梁性能有限元分析与研究［J］.机电产品开发与创新，2010，23(1).