钢带缠绕预应力模具缠绕过程的数值模拟*
2012-10-23陈孔军孔德军
陈孔军 王 强 赵 东 孔德军
(济南大学机械工程学院,山东济南 250022)
钢带缠绕预应力模具是采用高强度薄钢带作为缠绕材料,按照一定的张力变化模式对模具进行缠绕,在模具外侧形成数百乃至数千层的钢带缠绕层,用于替代年轮式预应力模具中的预紧环[1]。与年轮式预应力模具相比较优势明显,表现为:承载能力高,形状尺寸小;工件的尺寸精度高;模具的使用寿命提高[2-3]。
钢带缠绕是制造该模具十分关键的一步。钢带缠绕层的层数多达数百至数千层,若缠绕过程合适,能够使缠绕层外形紧凑,预紧力分布合理,各钢带内部应力波动幅度较小,可有效提高模具的疲劳强度,显著提高承载能力[1]。
在钢带缠绕模具设计制造过程中,为了能够得到缠绕钢带对模具产生的预紧力及模具的变形,比较经典的方法是将模具简化为厚壁筒进行力学性能分析,然后利用拉美公式计算其内应力和变形。但拉美公式适用的范围是平面应变问题,即假设厚壁筒无限长,忽略其轴向变形[4]。而常用的模具不可能轴向无限长,这样就不可避免地带来了误差,对模具的设计制造和使用产生了不利的影响。因此,利用有限元软件对钢带缠绕的过程进行模拟,得到预紧力的分布及模具的变形,对模具的设计制造和使用具有重要的意义。
1 模型建立
1.1 缠绕设备
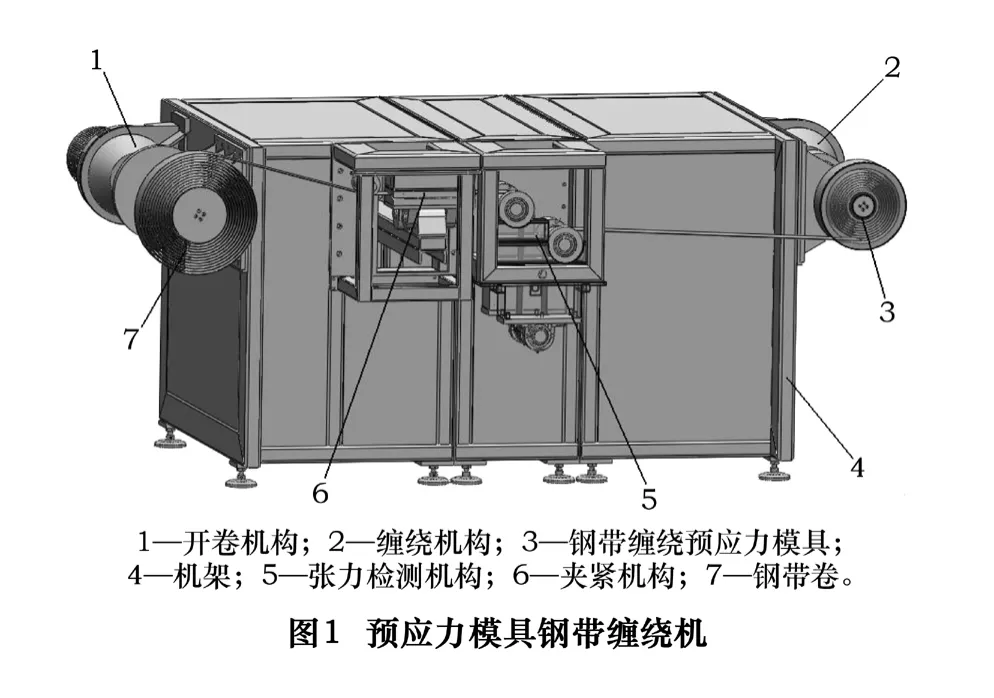
图1为一台钢带缠绕预应力模具制造设备[5-6]。该机采用双电动机式变张力缠绕系统,由开卷机构、夹紧机构、张力检测机构、缠绕机构、旋转编码器装置和电气控制系统等组成。开卷机构与缠绕机构分别水平安装在组合机身的左、右两侧,且保持轴线平行。机身部件采用模块式分体结构,能够满足预应力模具钢带缠绕过程中大张力、变张力的载荷特点[1]。
本文利用有限元软件ANSYS/LS-DYNA,对该设备的钢带缠绕过程进行模拟分析。
1.2 几何模型
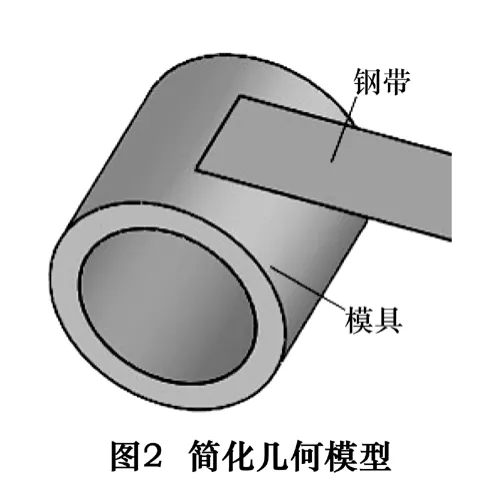
图2为钢带缠绕预应力模具的简化模型。圆筒内径为60 mm,外径为80 mm,高度为80 mm。利用共线的方式将模具和钢带连接,钢带宽度为40 mm,厚度为0.32 mm,初始设计钢带长度能满足缠绕20圈。为能与实际缠绕过程相符,如图3所示,在模具两侧建立两个夹持面,对夹持面施加转动载荷,以静摩擦的方式带动模具转动。

1.3 材料及机械性能
模具选用高强度钢45CrNiMoVA,钢带选用65Mn。两种材料的性能如下表1所示。

表1 材料机械性能表
1.4 网格划分
采用实体单元SOLID164以映射方式对模具划分网格,采用壳单元SHELL163对钢带和夹持面网格划分,如图3所示。
2 关键技术处理
2.1 定义接触
模拟中出现钢带和其自身相接触的情况,又因为钢带采用壳单元划分网格,不便于定义接触面和目标面。因此,模拟定义自动单面接触(ASSC),摩擦系数选用0.2。因为,单面接触适用于当一个物体的外表面与其自身接触或和另一个物体的外表面接触时,程序能够自动搜索接触面和目标面[7]。
2.2 边界条件
在钢带缠绕过程中,我们只允许模具绕轴线转动,不需要其他方向的转动和移动,所以我们在将夹持面和模具左右侧面建立接触后,要限制夹持面除绕轴线转动以外所有的自由度。
2.3 施加载荷
对夹持面施加定转动载荷2π/s,由夹持面带动模具同速转动。应在钢带的另一端施加定张力2 100 N。
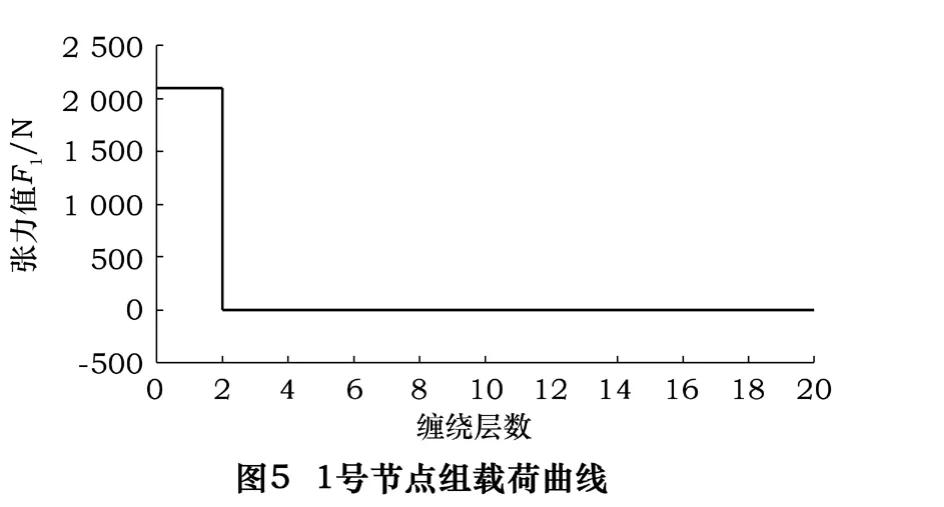
在模拟过程中,由于钢带过长,出现了抖动现象,所以对钢带实行分步加载的方式。如图4所示,在0~2圈内,张力施加在1号节点组上,其他节点组张力为零(图5);当2~4圈时,张力施加在2号节点组(图6);依此类推,每一步所施加的定张力为2 100 N,这样既解决了钢带的抖动问题又没改变定张力值。


2.4 解决沙漏问题
在模拟的初期,模具发生了非常严重的变形,如图7a所示,通常称之为沙漏现象。沙漏是一种以比结构全局响应高得多频率振荡的零能变形模式。沙漏导致出现一种数学上稳定,但物理上不可能的状态。它们通常没有刚度,变形呈锯齿形网格[6]。通过全局调整模型体积粘性,全局增加弹性刚度,局部增加弹性刚度,成功地解决了沙漏问题。图7是表示沙漏现象从有到无。

3 模拟结果分析
在解决以上问题的基础上,完成了缠绕20圈钢带的模拟。图8是钢带层等效应力等值线图,最大值为273 MPa,均未超过其屈服极限。

3.1 缠绕过程中预紧力变化趋势
以模拟数据为基础,选取图9中5338与5207号节点为分析对象(这两点位于模具外表面同一母线,5207为母线端点,5338位于中间位置;两者对比,能较好反映模具外表面预紧力),得到预紧力随时间的变化曲线,如图10所示。从图中曲线看,钢带缠绕的前几圈预紧力增加的速度明显比后几圈要快。例如,5 338号节点在前10圈预紧力增加速度为3.32 MPa/s,而后10圈增长速度只有0.89 MPa/s;同样,5207号节点在前10圈预紧力增长速度为1.91 MPa/s,而后10圈增长速度仅为0.59 MPa/s。


从图中得到两条曲线的变化趋势大体相同。即随着钢带缠绕圈数的增加预紧力的增长速度在减慢。因此,若要预紧力保持等速增长,则要使钢带所受张力以一定规律逐渐增大,这也佐证了钢带缠绕设备实现变张力缠绕功能的重要性。
3.2 预紧力分布规律
3.2.1 轴向分布
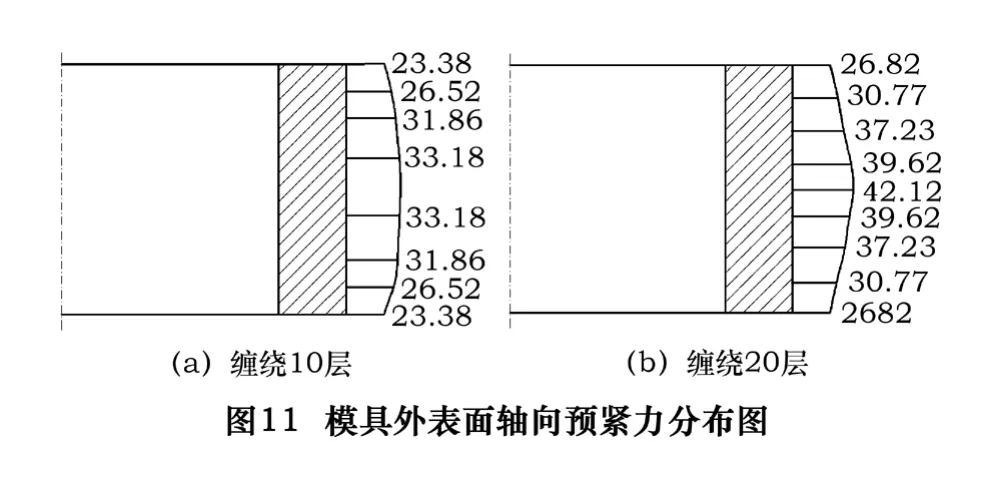
图11是模具外表面轴向预紧力分布图。从图中看出,预紧力在轴向分布是不均匀的,轴端处最小,然后逐渐增大,到中间位置,达到最大值。这种现象势必造成模具中间部位的预紧作用较强,而在两端有所减弱,我们称其为端部效应[4]。
3.2.2 周向分布
图12是图9中5207号节点所在的截面模具外表面周向方向预紧力分布图,横坐标表示各节点沿逆时针方向的圆角。从图中可看出,预紧力沿周向分布是不均匀的,具有一定的波动性,而且随着钢带层数增长这种波动性变得越来越明显。这验证了定张力缠绕情况下,内层钢带被外层钢带的“放松”效应。


3.3 模具内外表面径向位移
利用有限元软件的另一个目的是预测模具的径向位移,以便在真正的缠绕过程作为有效参考。图13表示图9中5338与7276号节点的径向位移变化曲线。从图中看到,在缠绕初始阶段模具径向位移较大且相对不稳定,说明这一阶段预紧力较不稳定;5圈之后,径向位移增速趋于稳定,相对应的预紧力也稳步增长。缠绕20圈以后,5338节点径向位移为0.105 2 mm,7276节点径向位移0.138 7 mm。两者相比,内径节点的变化量较大,这与拉美公式计算径向位移的公式相符。如式(1)所示,式中E、μ、b、a、P2均为常数,因此,r越大,径向位移u就越小。

式中:u为径向位移,mm;E为弹性模量;μ为泊松比;b为厚壁筒外径,mm;a为厚壁筒内径,mm;P2为预紧力,N;r为半径,mm。
4 结语
本文采用有限元软件ANSYS/LS-DYNA对钢带缠绕预应力模具缠绕过程进行了数值模拟,建立了其有限元模型,解决了模拟中出现的一些问题。根据数值模拟结果,得到以下结论:
(1)在定张力情况下,随着缠绕层数的增加,模具表面预紧力增长的速度在减小。如若要实现预紧力的持续增长,则要不断调整张力值。这佐证了钢带缠绕模具制造设备具有变张力缠绕这一功能的重要性。
(2)预紧力在模具表面沿轴向和周向分布具有不均匀性。轴向中部数值最大,两端值较小,由中间向两端逐渐减小,我们称之为端部效应。周向预紧力分布出现波动且波动程度随缠绕层数增长有所加剧。因此,利用有限元数值模拟,能够预测预紧力有效区域,提高材料利用率和模具寿命。
(3)模具表面节点径向位移,在前几圈时速度较快但不稳定,5圈过后以稳定速度增长。外表面节点径向位移小于内表面节点径向位移,与拉美公式相符。
[1]王强,何芳,杨晋穗,等.高强度高刚度钢带缠绕预应力模具[J].制造技术与机床,2011(5):29-32.
[2]王强,何芳,吴虔,等.钢带缠绕预应力模具与制造设备[J].模具技术,2010(5):151-153.
[3]来小丽,王强,蔡冬梅,等.钢带缠绕预应力模具缠绕层数的确定方法[J].塑性工程学报,2008,25(3):152 -156.
[4]蔡冬梅,王强,王鹏,等.类厚壁筒模具预紧结构预紧力的分布规律[J].组合机床与自动化加工技术,2008(5):26-29.
[5]王强,何芳,吴虔,等.预应力模具数控钢带缠绕设备及其控制方法:中国,ZL200910207978.4[P].2010 -05 -05
[6]张咸科,王强,吴虔.预应力模具钢带缠绕机结构设计与有限元分析[J].组合机床与自动化加工技术,2011(1):83-89.
[7]郝好山,胡仁喜,康士庭.LS-DYNA非线性有限元分析从入门到精通[M].北京:机械工业出版社,2010.
