含裂纹法兰接管的应力强度因子数值计算
2012-10-22何家胜朱晓明
何家胜,魏 卫,朱晓明,陈 伟,张 林,杨 峰
(1.武汉工程大学机电工程学院,湖北 武汉 430074;2.中国石油化工股份有限公司武汉分公司,湖北 武汉 430082)
0 引 言
法兰连接是炼油装置中连接设备与管路的常见元件.由于炼油过程中腐蚀性介质的影响,接管与法兰连接处环焊缝高应力区容易发生开裂,给管路运行造成重大安全隐患.对于这种情况往往只能采取临时补焊或整体打包等方式进行处理,如图1、2所示.为了确保装置的长周期安全运行,有必要对含裂纹的法兰接管情况进行断裂力学参数分析,为装置的安全评定提供参考依据.

图1 补焊处理的接管法兰Fig.1 The welded nozzle flange

图2 整体打包处理的接管法兰Fig.2 The overall packaged nozzle flange
下面利用有限元方法对法兰接管组合结构环焊缝处的应力强度因子进行分析.
1 含裂纹的法兰接管有限元分析
1.1 概 述
裂纹应力强度因子的计算方法有三大类:解析法、数值法和实验方法.解析法只能计算简单裂纹,对于复杂结构的裂纹难以获得精确解析解[1-3].实验方法是能解决一些较复杂的裂纹问题,但是实验法在裂纹模型预制和裂纹前沿多点数据测量上还存在不足[4].数值方法中的三维有限元法以其强大的模拟和数值计算功能已经被广泛用于应力强度因子的计算[5-10].
设r为裂纹尖端附近某点到裂纹尖端的距离,因裂纹尖端应力的各个分量都与成反比,当r趋近于0时,在裂纹尖端,应力的各个分量都会趋于无穷大,如图3所示,这种特性就叫做应力奇异性.
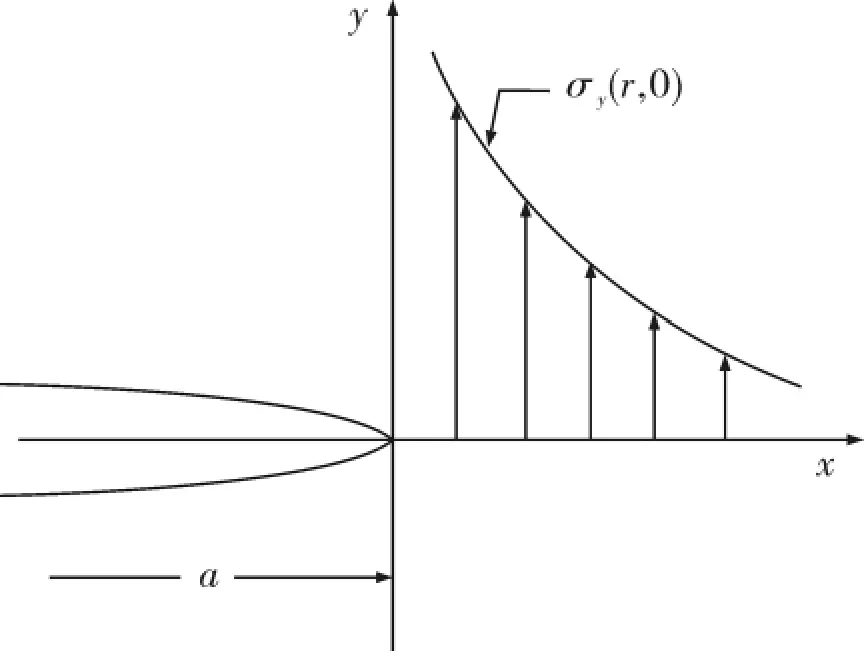
图3 裂纹尖端应力奇异性Fig.3 Stress singularity in the model of crack tip
由于裂纹尖端应力奇异性,为获得较高的计算精度,采用比较成熟的节点法.该方法采用奇异单元,该单元是使围绕裂纹尖端的第一圈等参单元各边的中间节点移到离裂纹尖端的处[11].
1.2 有限元模型的建立
研究对象为脱硫系统换热器401/2壳程上方的法兰及接管,如图4所示.法兰上方焊接弯头接管,在环焊缝处产生了角度为α的穿透性裂纹,如图5所示.该法兰为PN2.5级带颈对焊管法兰,弯头接管内半径r为75mm,壁厚t为4.5mm,弯曲半径RM为225mm,弯头另一端接长度为1000mm的直管,材料都为20号钢.

图4 法兰弯头接管结构Fig.4 The Structure of nozzle flange
1.2.1 建立裂纹尖端奇异单元 对于三维裂纹,其奇异单元不能自动生成,必须采用手动建立.因此建模时采用自下而上的建模方法,先建立节点,再由节点生成单元.在裂纹前沿沿其长度方向平分为9段,即形成10层节点,每一层节点是以裂纹尖端节点为圆心,形成10圈同心圆节点,如图6所示,通过连接各个节点生成裂纹前沿单元,所有的单元都是8节点的Solid45单元.然后将围绕裂纹前沿的第一圈单元转化成奇异单元.
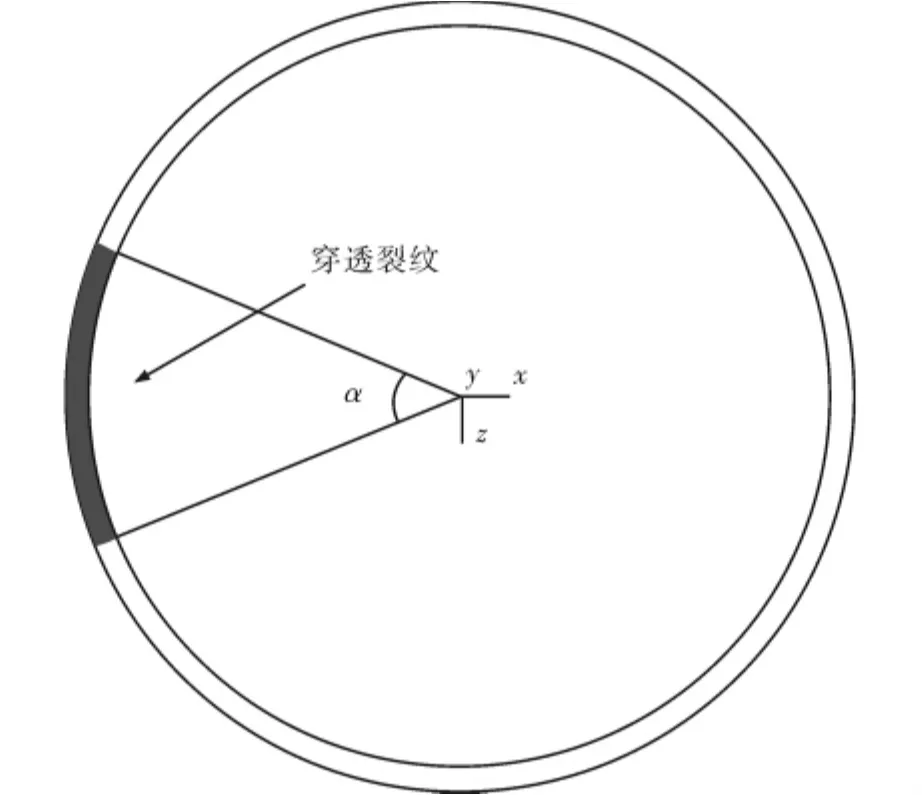
图5 法兰弯头接管裂纹横断面Fig.5 The crack cross-section of nozzle flange

图6 裂纹尖端奇异单元Fig.6 The singular element in the model of crack tip
1.2.2 法兰接管整体模型的建立 采用实体建模,建立法兰接管实体模型,并划分网格.接着采用节点耦合的方法,将裂纹前沿最外圈节点与整体模型裂纹前沿连接处的节点进行耦合,得到含裂纹法兰接管实体模型的有限元模型,如图7所示.
1.3 施加边界条件
力边界条件:在法兰与接管内表面施加内压P内=1.1MPa,同时在直接管的右端面,沿接管轴向即x轴正方向,施加由内压所产生的轴向载荷P轴=9.167MPa.

图7 裂纹整体有限元模型Fig.7 The finite element model of crack
位移边界条件:在法兰的下端面对其位移施加全约束,即对其施加x、y、z三个方向的位移约束.具体边界条件施加情况,如图8所示.
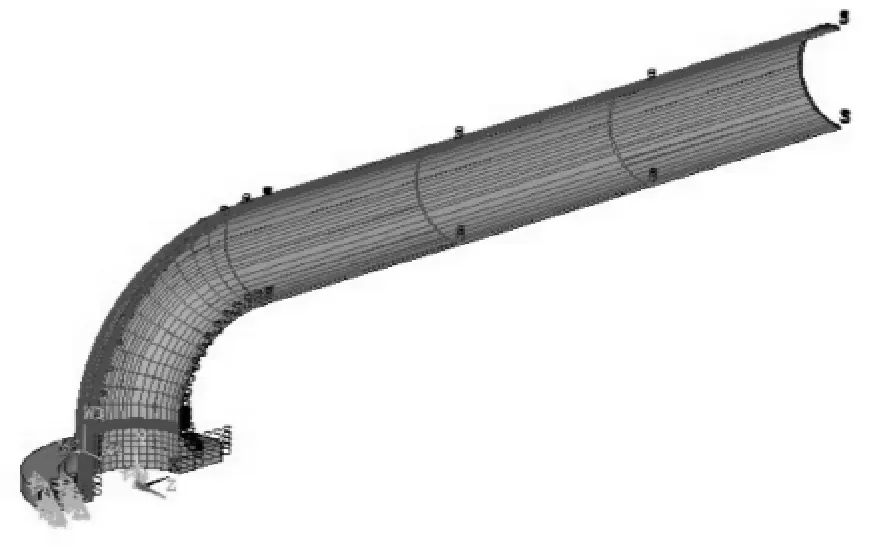
图8 接管法兰边界条件Fig.9 The boundary conditions of nozzle flange
1.4 计算应力强度因子
施加边界条件求解后得到裂纹前沿各处的应力强度因子,裂纹前沿共有10个节点,如图9所示.
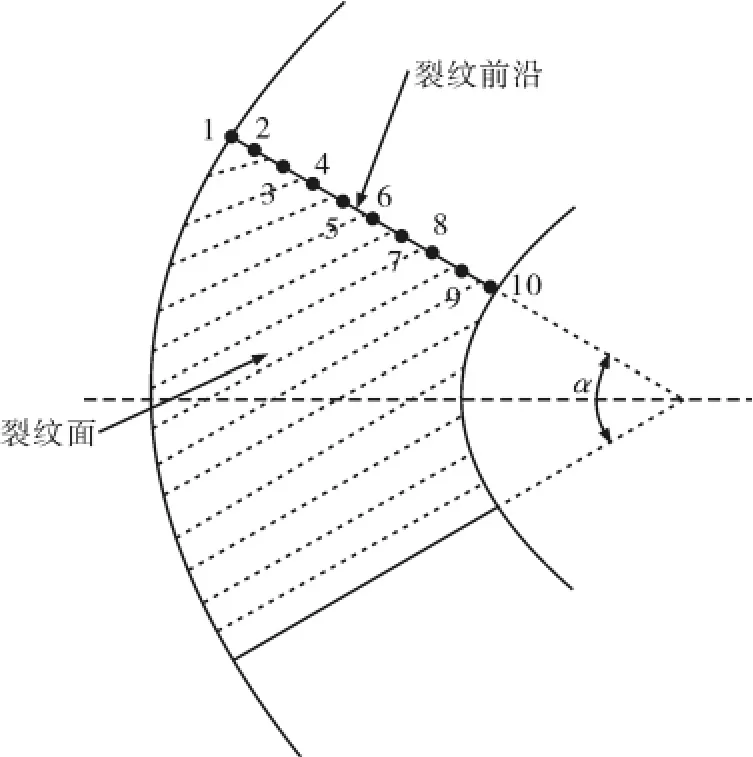
图9 有限元模型中裂纹前沿节点示意图Fig.9 The nodes at the front of crack in the finite model
依次求得各处节点Ⅰ型裂纹的应力强度因子KI,总共计算了7组不同裂纹角度的数据.结果如表1所示.
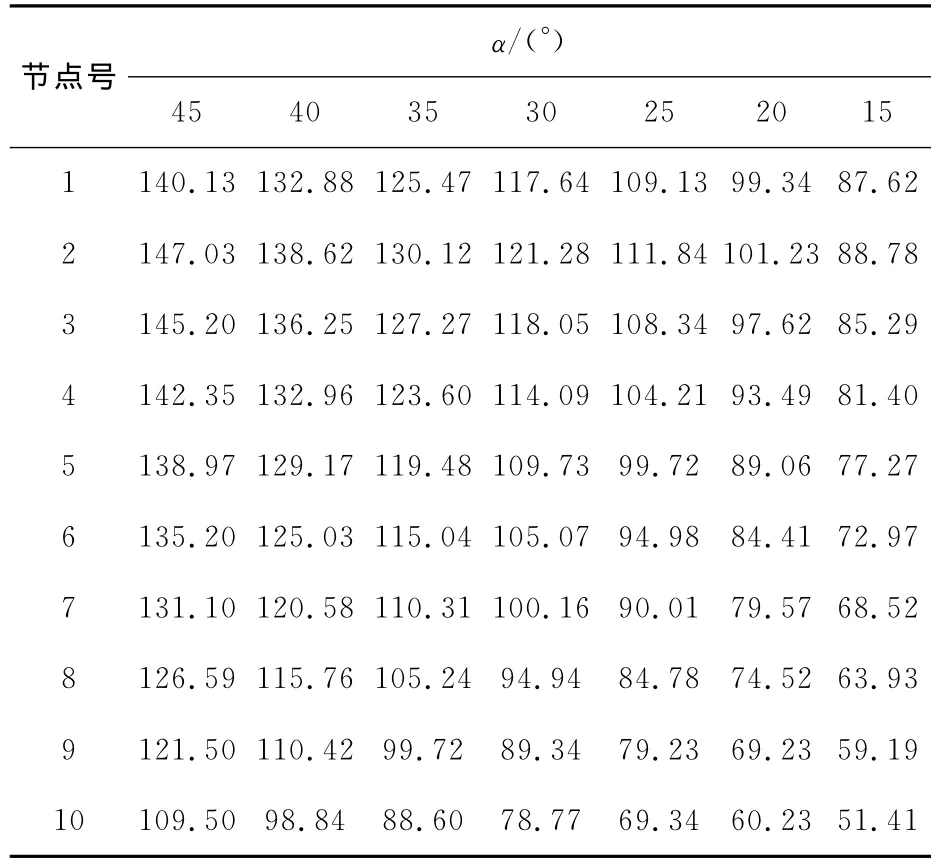
表1 裂纹前沿各节点应力强度因子KITable 1 Stress intensity factor at the front of crack,KI MPa·mm1/2
从表1中可知,Ⅰ型裂纹的应力强度因子KI的最大值在裂纹前沿靠近法兰接管的外表面处.KI结果分布如图10所示.
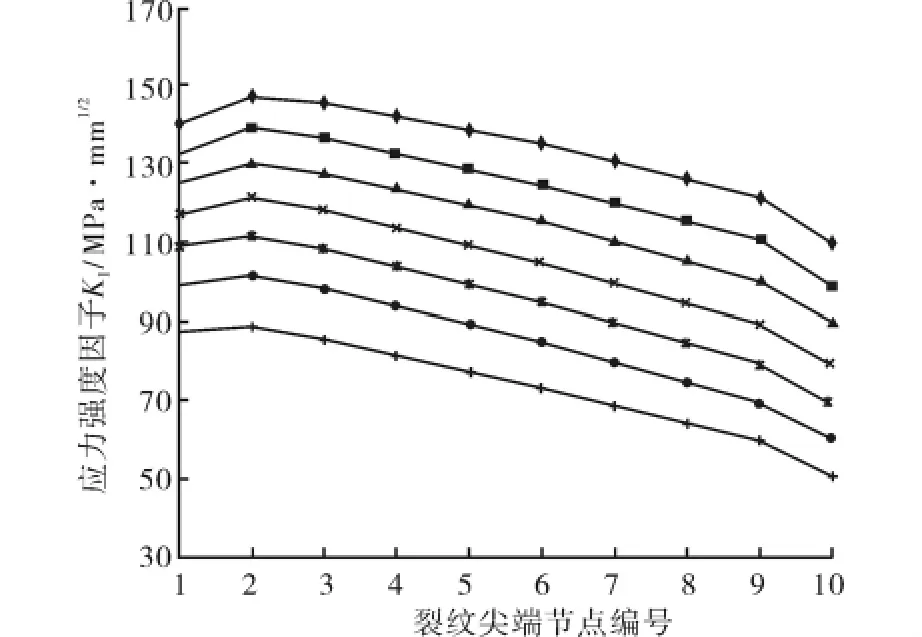
图10 裂纹前沿各节点应力强度因子KIFig.10 Stress intensity factor at the front of crack ,KI

从图10中可以看出,裂纹前沿的KI值基本呈倒“U型”分布,内表面处的应力强度因子值要比外表面的小得多;应力强度因子的最大值在裂纹前沿靠近法兰接管的外表面处.根据上面的结果可以推测,当裂纹要继续扩展时,裂纹前沿靠近法兰接管外表面处的KI最先达到材料的断裂韧度KIC,即裂纹在靠近法兰接管外表面处较先扩展.应力强度因子是判断裂纹是否扩展的主要参量,而在目前又无法得到复杂裂纹前沿应力强度因子解析解的情况下,通过数值模拟的方法求出复杂裂纹前沿各点应力强度因子的近似解,再结合平面应变断裂韧度KIC的变化规律及裂纹扩展判据KI≥KIC,就能定量的判断裂纹扩展情况.该结论对含缺陷压力容器及管道的安全评定具有重要的数据价值.
2 结 语
a.通过节点建模法及在裂纹前沿设置应力奇异单元建立了含穿透裂纹法兰接管的有限元分析模型.
b.通过有限元计算得到了不同裂纹长度的裂纹前沿各处的应力强度因子KI的数值解,根据计算得到的数据确定了裂纹前沿应力强度因子的分布情况并确定了最大应力强度因子的位置.
c.上述计算得到的含穿透裂纹法兰接管的应力强度因子数值解可用于含缺陷压力容器及管道的安全评定.
[1]尹峰,王伟,宁纯利.表面裂纹理论的回顾与评述[J].飞机设计,2003(2):27-33.
[2]Underwood J.Stress intensity factor for internally pressurized thick walled cylinders.Stress analysisand growth of cracks[J].Society for Testing and meterials 1972(513):59-70.
[3]徐振兴.断裂力学[M].湘潭:湘潭大学出版社,1985:59.
[4]徐一耿.接管拐角裂纹应力强度因子解的理论探讨[J].浙江丝绸工业学院报,1995(4):42-46.
[5]黄佩珍,师俊平.求解界面裂纹应力强度因子的高次权函数法[J].固体力学学报,2000(2):166-170.
[6]黄士振.厚壁圆筒半椭圆表面裂纹应力强度因子的有限元计算[J].华东工业学院学报,1990(4):90-94.
[7]梁文军,金志江.表面裂纹应力强度因子计算及扩展跟踪的权函数法[J].工程设计学报,2001(2):69-72.
[8]龙靖宇,王宏波.基于有限元法的二位裂纹应力强度因子研究[J].武汉科技大学学报:自然科学版,2005(3):244-246.
[9]朱光强.圆筒表面椭圆裂纹复合型应力强度因子有限元分析与研究[D].武汉:武汉工程大学,2007.
[10]何家胜,谢飞,朱晓明.圆柱壳内表面椭圆裂纹应力强度因子数值计算[J].武汉工程大学学报,2011,33(11):70-73.
[11]李翠华.计算应力强度因子的奇异单元法[J].西安交通大学学报,1991,25(6):23-28.
