反演设计对束晕-混沌束包络的非线性反馈控制

华能曲阜电厂 闫华龙

反演设计对束晕-混沌束包络的非线性反馈控制

华能曲阜电厂 闫华龙

能源危机是全世界面临的重大问题之一，如何利用新能源造福社会是科研工作者的历史使命。目前核聚变能已成为一种世界公认的未来清洁型能源，核能的高效性可以充分满足人类社会生产和生活的需要，具有极大的推广价值。为了使得核电系统能发挥其最大利用空间，科学家提出了以加速器为驱动的放射性洁净核能系统（ADS），它把加速器和反应堆结合起来，是一种更安全、更洁净的新一代核能系统。

然而该系统对加速器的要求极高，一些实验研究成果和理论模拟计算都已发现，在强流加速器的低能传输段，束流会产生一个比束核半径大得多的低密度晕圈，我们将该现象称为束晕–混沌现象。束晕–混沌现象是目前强流粒子束应用中所面临的困难问题之一。因此，对束晕–混沌及其控制的研究有着重要的理论和实际意义。

反演设计方法是一种基于Lyapunov稳定性条件的递推设计方法，近年来，该方法在非线性控制领域有着十分广泛的应用。反演设计方法的主要思想是：在对具有反馈形式的非线性系统进行控制时，从非线性系统的输出变量向控制输入变量“反演”，进而得到一系列反馈控制律及相应的Lyapunov函数，由此构造反演反馈控制器，实现对非线性系统的渐近稳定控制。

一、束包络半径的数值模拟

令 d rb/d s＝ρ，则周期聚焦通道中满足K–V分布的粒子束归一化包络方程如下形式：

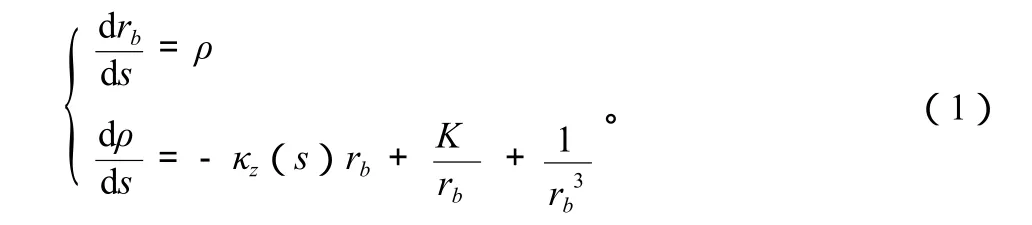
式（1）中，K为束导流系数，κz（s）为聚焦场的幅度，rb为束匹配半径。选取适当的参数：周期聚焦场的占空比η＝0.4，束导流系数K＝0.903 2，聚焦场的幅度大小κz（0）＝10.07，束匹配半径rb0＝0.789 1。取积分步长为0.02，初始条件rb（0）＝1.578，ρ（0）＝1。用四阶龙格–库塔法对式（1）进行数值求解，得到如图1所示的束包络半径的相轨道。

图1 束包络半径的相轨道

二、反演设计反馈控制器

假设存在一个控制器u（s），在该控制器作用下，包络方程变为：

以束包络匹配半径rb0为控制目标，为了得到假设的控制器u（s）的具体表达形式，引入粒子束包络半径的控制误差e1，e1按下式计算：

对上式两边求导，得

引入变量a1，并令a1＝－b1e1，其中b1＞0，且b1作为控制调节因子。分别定义变量e2和Lyapunov函数V如下：

对式（5）两边求导，得e2′＝ρ′－a1′。

利用式（5）和式（5），可推导出Lyapunov函数V的导数：

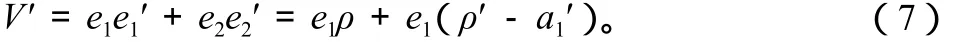
将式（5）带入上式，得

当式（9）成立时，V′≤0恒成立。因此在Lyapunov函数稳定性条件下，rb→rb0，控制目标将得以实现。根据式(2）和式（9）可推导出K–V分布条件下控制周期聚焦场强流粒子束包络混沌运动的非线性控制器u（s）的表达式：

三、对束包络的反演反馈控制数值模拟

设置控制参数因子b1＝10，对束包络受控方程（2）实施控制。为了便于比较有无控制时的不同效果，先让方程式（2）自由演化3 000个积分步长后，再采用式(10）所示控制器实施控制。束包络半径rb与控制目标rb的误差函数随时间演化的情况如图2所示。由图2可知，未加控制时，误差函数（束包络半径rb与控制目标rb0的相对距离）无规则振荡，即束包络半径的径向运动处于混沌状态。施加控制后，rb与rb0之间的相对距离很快收敛，并一直稳定在0附近，这说明粒子束包络半径被稳定控制在束匹配半径上，有效达到了控制目标。

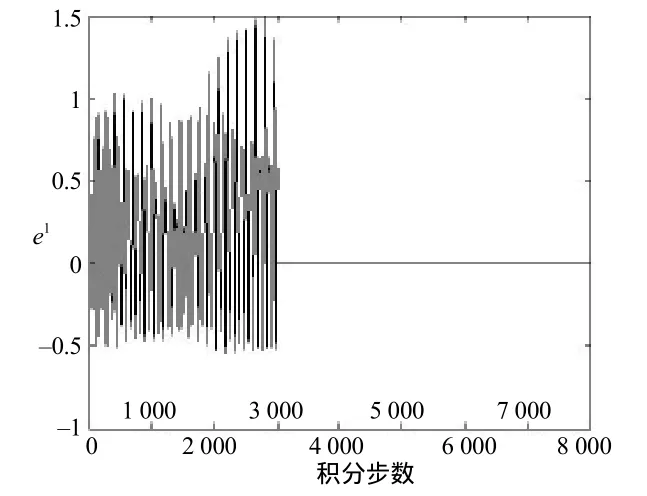
图2 包络半径误差的时间演化

四、结论

综上，反演设计非线性反馈控制方法以Lyapunov函数的稳定性理论为依据，能较好地把处于混沌状态的失匹配束包络半径稳定控制到匹配半径，具有较快的起控速度， 对于强流加速器驱动的放射性洁净核能系统（ADS）领域的研究有着积极的意义。