运动模糊图像方向角的估计方法研究

加春燕，王建丽，刘 鹏

(1.北京工业职业技术学院，北京 100042;2.太原科技大学华科学院，太原 030024;3.山西农业大学信息学院，山西 太谷 030800)

在获取数字图像的过程中，由于设备或者操作者的原因，易造成运动模糊。如果在曝光瞬间，相机镜头和对象之间有相对运动，那么拍摄到的图像便是运动模糊图像。简单的线性运动模糊模型可用一个卷积型方程表示[1]:

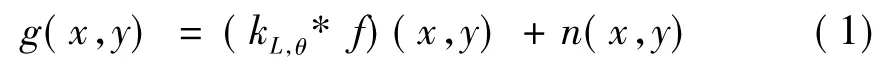
其中，g表示运动模糊带噪的图像，f是未受到运动模糊和噪声影响的理想图像，kL，θ代表运动模糊的点扩散函数(PSF)，n通常视为高斯白噪声。复原运动模糊图像的目的就是:从观测图像g出发，结合运动模糊的点扩散函数kL，θ和噪声n的相关信息，得出复原图像，复原结果与f越接近越好。

运动模糊的点扩散函数 kL，θ的一般表达式为[2]:

显然，确定kL，θ的关键在于两个重要参数:一是运动模糊的方向角θ，二是运动模糊的长度L.要进行图像复原，需要准确地估计出θ和L，本文主要研究运动模糊图像的方向角θ的估计方法。

1 运动模糊图像的频谱特征分析

图1 运动模糊图像及其Fourier频谱图像Fig.1 A motion blurred image and its Fourier spectrum image with L=10 pixels and θ =45°

由卷积原理，对模型方程(1)做Fourier变换，得到频域上的方程:

其中K(u，v)为一个Sinc函数，因此，如果运动模糊图像受噪声污染较小，则相应的Fourier频谱图像中会出现平行的黑线，且该组黑线与Y轴的夹角即为运动模糊方向角θ[3].图1中左边为运动模糊图像，其中方向角为45°，右边是对应的频谱图像G(u，v)，从中明显看出平行线的特征，且平行线与Y轴的夹角约为45°.显然，频谱图像中的平行黑线是估计θ的重要依据，后面涉及到的方法都是从运动模糊图像的频谱特征出发来估计θ.

2 方向角估计方法的对比研究

2.1 Hough 变换方法

Hough变换通过检测图像中点的共线性来确定图像中最为明显的直线[4]。具体来说，假设图像中有n个特征点，希望找出含特征点最多的直线。1962年数学家Hough提出了一种简单方法:将平面内过一点的所有直线转化为参数空间中的一条正弦曲线，如果参数平面内有K条正弦曲线相交于一点，则对应XY平面内K个点共线[7]。Hough变换检测图像中直线的数值实验过程为:

(ⅰ) 网格剖分 ρ∈ [ρmin，ρmax]，θ∈ [θmin，θmax]，在 ρθ平面形成网格;

(ⅱ)在ρθ平面每个网格放置一个记数器A(ρ，θ)，并设置初值均为0;

(ⅲ)对图像中的每个特征点(xi，yi)，依次取θ= θmin∶θmax，之后计算出ρ=xicosθ+yisinθ，于是该网格记数器A(ρ，θ)增加1;

(ⅳ)所有特征点都统计完成后，找到值最大的记数器(比如记为 A(ρ*，θ*)，则对应 XY平面中检测出的直线方程为 ρ*=xcosθ*+ysinθ*.

在实际运用中，通常先得到模糊频谱图像的边界图像(二值图像)，选取边界点为特征点，再做Hough变换。图2展示了用Hough变换检测运动模糊图像方向角的效果，其中(a)图是运动模糊图像，θ=30°，(b)图显示了Hough变换检测出的直线，对应角度为 30.809°，(c)图中运动方向角 θ=90°，(d)图检测出的结果为90.001°.

2.2 Radon 变换方法

对于函数 G(u，v)，其 Radon 变换为[5]:

图2 Hough变换估计运动模糊图像的方向角Fig.2 Estimation for angle of motion blurred images by using Hough transform

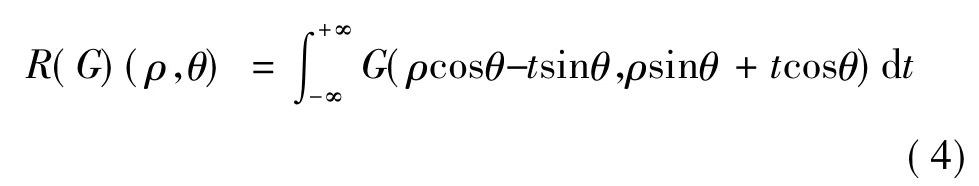
事实上，G(u，v)的Radon变换是沿着距原点(图像中心)ρ且与Y轴夹角为θ的直线的积分，Radon变换的最大值对应图像中最明显的直线，该直线的角度即为运动模糊图像方向角的估计值。需要注意的是，Radon变换要计算函数沿各个方向直线的积分，而对于有限的图像(一般是矩形)来说，显然图像对角线上的线段最长，积分结果会比较大，因此用Radon变换常常错误的估计出45°或者135°，为了克服这种现象，可以对图像预先归一化，即逐点除以和图像大小相同的全1矩阵，再进行Radon变换。

图3展示了对运动模糊频谱图像做Radon变换的结果，左边是运动模糊频谱图像，其中θ=10°，右边是Radon变换的结果，图像中最亮的地方对应角度为10.052°，估计比较准确。

图3 Randon变换估计运动模糊图像的方向角Fig.3 Estimation for angle of motion blurred images by using Radon transform

2.3 Cepstral变换方法

Cepstral变换方法通过计算模糊图像的对数逆频(Cepstrum)来寻找特征[6]。模糊图像 g(x，y)的对数逆频定义为:

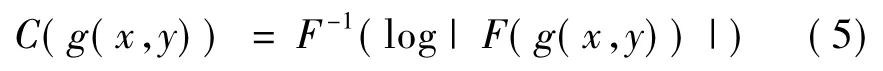
对数逆频的一个重要性质是卷积可加性，假设不考虑噪声，即在式(1)中n(x，y)=0，则:

图4 Cepstral变换估计运动模糊图像的方向角Fig.4 Estimation for angle of motion blurred images by using Cepstral transform

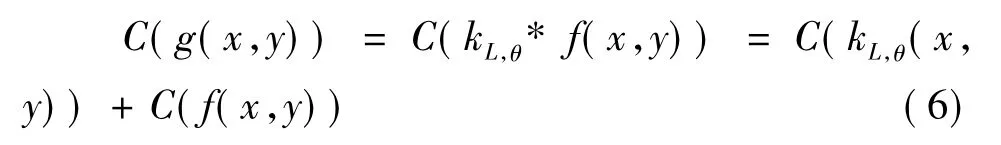
模糊核函数kL，θ的Fourier变换K(u，v) 是一个Sinc函数，且在 ±1/L 处值为0[4]，于是log|K(u，v)|在 ±1/L处为负无穷大，从而 C(kL，θ(x，y)) 在距原点L处是负无穷大，由于对数逆频的卷积可加性，则这个性质会保留到C(g(x，y))中，即从C(g(x，y))的图像中看，在距原点L处应该有两个大的负峰。因此，要估计运动方向角，只需从第一个峰值处到原点画一条直线，再计算该直线的倾斜角即可。

图4展示了用Cepstral变换估计运动模糊图像方向角的过程。左边是运动模糊频谱图像G(θ=60°)，中间是对数逆频图像 C(g(x，y))，从中确实可以看到两个明显的负峰。右边从一个峰值处检测到的直线，该直线的倾斜角为60.213°，与θ的真实值十分接近。

3 三种方法实验结果的综合分析比较

为了对Hough变换、Radon变换和Cepstral变换三种方法进行综合分析比较，利用matlab数学软件编写程序，进行了大量的数值实验。测试图像为256×256的卫星图像(如图1所示)，方向角的变化范围是0°～180°，分别设定运动距离L=10和L=40两种情况来测试三种方法对L的敏感度，此外，定义信噪比SNR(见公式7)来衡量噪声水平，从定义可知，SNR越小代表噪声越大，试验中分别取无噪声和SNR=20两种情况来测试三种方法对噪声的敏感度。

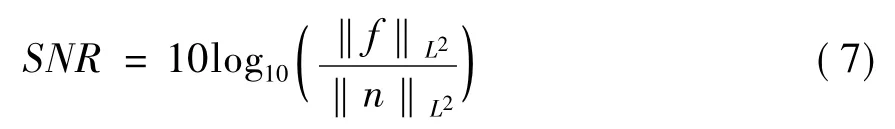
表1 无噪声时三种方法估计精度的数值结果Tab.1 Numerical results of three methods with no additive noise

图5 无噪声时三种方法的估计精度Fig.5 Estimation accuracy of three kinds of methods with no additive noise

表1和图5分别展示了无噪声时三种方法的估计精度(误差的绝对值)结果，容易看出，L=10时，Cepstral变换的估计效果最好，其次是Hough变换和Radon变换。而当L=40时，Radon变换的效果最好，其次是 Cepstral变换，Hough变换效果最差，误差高达12°.

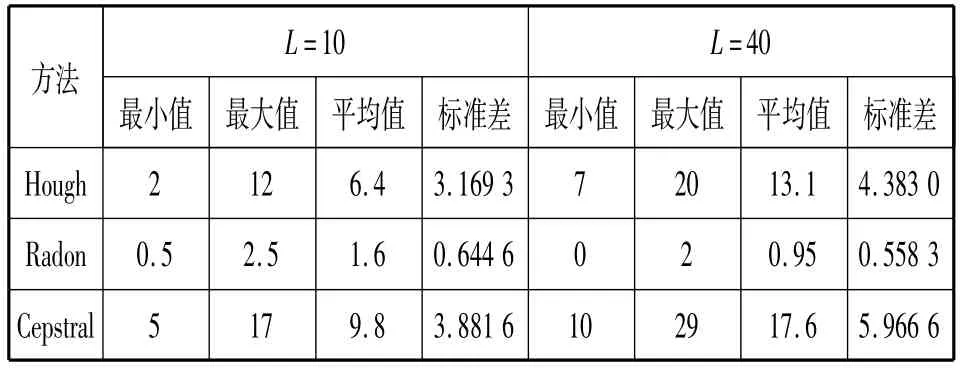
表2 SNR=20时三种方法估计精度的数值结果Tab.2 Numerical results of three methods with SNR=20

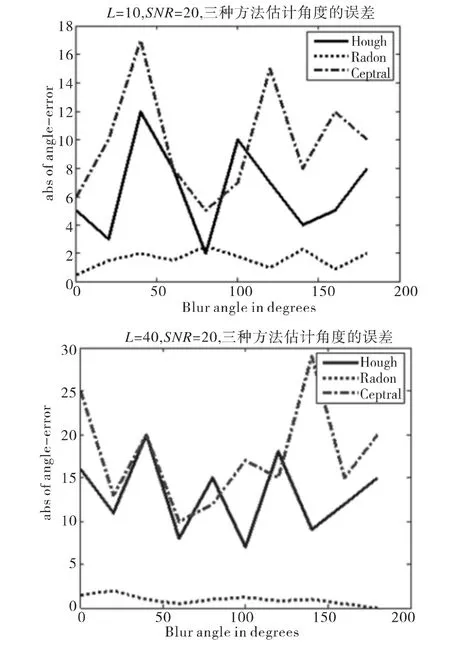
图6 SNR=20时三种方法估计角度的误差绝对值Fig.6 Estimation accuracy of three kinds of methods with SNR=20

表2和图6分别展示了信噪比SNR=20时三种方法的估计精度结果，有了噪声的干扰，估计角度的难度增加，但从结果容易看出，Radon变换的估计效果仍然很好，可见噪声对其影响不大。而Hough变换和Cepstral变换则对噪声比较敏感，平均误差在6.4°～29°之间，精度太低，不适宜估计角度。

根据第2节的原理分析和第3节的数值实验结果，可以得出如下结论:

(1)Hough变换:依赖于选取的特征点，特征点选不好则估计误差大[8]。对于小距离和无噪声干扰的情况，相对容易找到特征点，因此估计效果较好，而当运动距离增大或者加入噪声，则不易找到准确的特征点，从而导致估计结果较差。

(2)Radon变换:整体估计效果较好，噪声干扰对其估计精度的影响不大，且L较大时估计更为准确。

(3)Cepstral方法:运动距离L的大小对其估计精度影响不大，但它对于噪声比较敏感，噪声水平较高时估计不准确。

综上所述，对于给定的运动模糊图像，如果容易找到特征点，可用Hough变换来估计运动角度，反之则失效。假如图像受噪声污染较小，可以选用Cepstral变换方法，反之则用Radon变换方法。在实际的运动模糊图像处理中，由于噪声污染几乎不可避免，且图像千差万别，特征点不易选取，因此，最常用也相对实用的还是Radon变换方法。

4 结语

从运动模糊图像出发，结合其点扩散函数，分析了图像的频谱特征，之后研究了目前估计方向角常用的方法:Hough变换、Radon变换和Cepstral变换，通过分析每种方法的数学原理，结合大量的数值实验，综合比较了三种方法的估计精度，得出了三种方法的适用范围，有助于更为准确地估计运动模糊图像的方向角，进而较好地复原图像。

[1]CHAN T F，SHEN J.Image processing and analysis[M].Philadelphia:SIAM，2005.

[2]孙兆林.Matlab 6.x图像处理[M].北京:清华大学出版社，2002.

[3]LOK HANDE R，ARYA K V.Identification of parameters and restoration of motion blurred images[J].Chinese Journal of Computers，2007，30(4):686-692.

[4]LI Q，YO SHIDA Y.Parameter estimation and restoration for motion blurred images[J].IEICE Transactions on Fundamentals of Electronics，Communications and Computer Sciences，1997，20(8):14-30.

[5]MOGHADDAM M E，JAMZAD M.Finding point spread function of motion blur using radon transform and modeling the motionlength [J].In Proceedings of the 4th IEEE International Symposium on Signal Processing and Information Technology，2004，25(2):310-314.

[6]LOKHANDE R，ARYA K V，GUPTA P.Identification of parameters and restoration of motion blurred images[J].Proceedings of the 2006 ACM symposium on Applied computing，2006，10(3):301-315.

[7]陈高华，卓东风，夏锡瑞.基于Hough变换直线检测中的峰值提取[J].太原科技大学学报，2006，27(4):256-258.

[8]张凤珍，董增寿.基于数学形态学与Hough变换的道路边缘提取[J].太原科技大学学报，2010，31(3):193-196.