舰船非通视短基线方位角测量方法研究*
2012-10-16段静玄吴岳松操建闻
陈 辞 段静玄 吴岳松 操建闻
(1.海军驻426厂军事代表室 大连 116002)(2.中国舰船研究设计中心 武汉 430064)
1 引言
在舰船施工和对准作业过程中,两点的连线能够确定一条基线,基线可以是刻线或者标志板,基线与正北的夹角称为该基线的方位角。基线的方位角测量是舰船对准工作中的重要步骤,在舰载设备安装、调试以及舰艇对准等过程中具有重要的意义,例如:测量舰船艏艉基线的方位角,可作为标定舰船导航系统航向的参考真值,而航向精度将直接影响武器的作战性能[1];测量火炮等武器的射击基线方位角,可以使火炮根据首发射击效果对间接瞄准射击的发射方位角进行校正[2];测量卫星通讯设备、卫星气象设备等安装基座基线方位角,可以标定设备的零位,使其能够更准确的瞄准所需要的卫星。当标识基线的两点具备通视条件时,一般可以采用陀螺经纬仪来确定基线方位角[3];当不具备通视条件时,若标识基线的两点距离较远,且两点与GPS卫星通视条件较好时,可以使用差分GPS直接测量出基线的方位角[4~5]。
在某型舰卫星设备对准作业中,需要测量基线被不透明的物体遮挡,且基线又比较短,既不满足使用陀螺经纬仪测量的通视条件,又不能满足使用差分GPS测量的距离要求,或者两基准点与遮挡物距离较近,使得GPS不能很好的接收卫星信号。
为了解决这种在非通视条件下短基线测量的难题,本文利用现有舰船对准中常用的测量仪器:差分GPS系统、全站仪[6]、反射棱镜,提出了三种间接测量基线方位角的方法,分析了三种方法的精度和适用情况,并在某型舰卫星设备安装基线测量中得到了实际应用。
2 某型舰卫星设备外观图
如图1、图2所示,某型舰的卫星设备的侧视和俯视情况,在卫星设备的底部安装基座上刻有两个标识该设备安装基线的标志点A、B,A、B两点的连线穿过安装基座表面,在卫星天线罩安装后有少许延长。为了确定卫星设备安装方向零位,需要测量A、B两点连线与正北的夹角,即设备安装基线的方位角。A、B两点被该设备的球形天线所遮挡,不具备通视条件,设备底部直径即AB的距离约4m,距离相对较短,使用差分GPS测量难以得到满足精度要求的基线方位角。
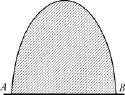
图1 某型舰卫星设备的侧视图
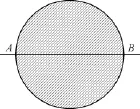
图2 某型舰卫星设备的俯视图
该卫星设备已经安装在舰艇的上层建筑,位置较高,有大面积的开阔地带与之具备通视条件。如果能够通过测量某基线至A、B两点距离量、角度量,便有可能通过三角函数关系推导出卫星安装基线的方位角。
3 测量方法
针对该型舰卫星设备以及周边环境的情况,下文给出三种基线方位角测量方法和计算过程。
3.1 方法一(平移法)
如图3所示,将A、B两点平移至具备通视条件的C、D两点,使平移的距离AC等于BD,利用直角器保证CA、DB均垂直于AB,使得CD与AB平行。使非通视基线测量转化为通视基线的测量。
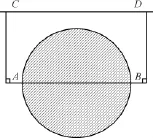
图3 平移法
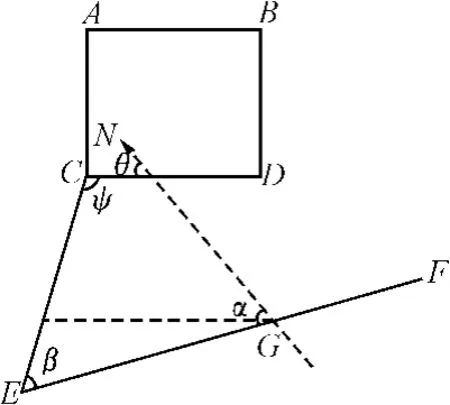
图4 平移法测量图
如图4所示,根据文献[7]介绍的方法,在舰船所在船坞外空旷处选择两点E、F,E、F的距离大于100m,E点与C点具备通视条件。在E、F两点架设差分GPS系统,可测得EF与正北夹角α[8],在C、E两点架设经纬仪,分别瞄准D、F两点后置零后再相互瞄准,可测得ψ、β,已知α、ψ、β,由几何关系有:

若C、D两点具备陀螺经纬仪的作业条件,也可以采用陀螺经纬仪直接测量出CD的方位角。
因直线AB与CD平行,θ即被测基线AB与正北的夹角。
平移法要求基线必须穿过天线,在天线底部A、B两点有部分延伸,且设备所在甲板面上存在能够平移的空间。
该方法计算简单,但对平移的操作过程要求较高,平移产生的误差是总测量误差的主要误差源。
3.2 方法二(三角形法)
如图5所示,A、B为确定卫星设备的安装基线的两点,在舰船所在船坞外空旷处选择一点C,该点与卫星设备天线底部A、B两点具备通视条件,使得C、A,C、B满足使用全站仪测量的条件;C点与A点的距离大于100m,使用差分GPS测量出AC的方位角。
A′B′为被测基线AB 在大地水平面上的投影,在A、B两点架设反射棱镜,在C点架设全站仪,以全站仪瞄准A点棱镜,可测量出AC的距离和仰角α,将全站仪水平角置零后瞄准B点棱镜,可测量出BC的距离和仰角β、水平角γ。在A、C两点架设差分GPS系统,可测量出A′C 与正北的夹角ψ。已知AC、BC、α、β、γ,根据余弦定理有:
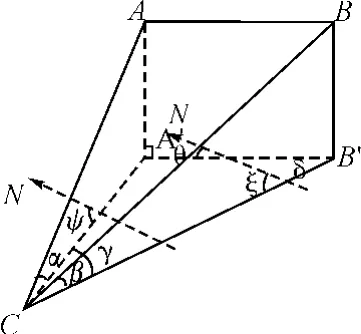
图5 三角形法测量图

θ即被测基线AB与正北的夹角。
三角行法要求A、B两点能够架设反射棱镜,C点必须能够同时与A、B两点通视,A、B两点中至少有一点能够架设差分GPS,且能很好地接收到GPS卫星定位信号。
3.3 方法三(四边形法)
如图6所示:A、B为确定卫星设备安装基线的两点,在舰船所在船坞外空旷且高差较小的地带选择两点C、D,两点相距100m以上,C点与卫星设备天线底部A点具备通视条件,D点与卫星设备天线底部B点具备通视条件。
A′B′为基线AB在大地水平面上的投影,在A、B两点架设反射棱镜,在C、D两点架设全站仪,以C点全站仪瞄准A点棱镜可测量出距离AC和仰角ζ,以D点全站仪瞄准B点棱镜可测量出距离BD和仰角κ,两全站仪相互瞄准可得到水平角ψ、β,通过在C、D两点架设全站仪和反射棱镜可测得距离CD,在C、D两点架设GPS测量系统,可测量CD与正北夹角λ。已知AC、ζ、BD、κ,根据余弦定理有:

图6在大地水平面的投影如图7所示。

图6 四边形法测量图
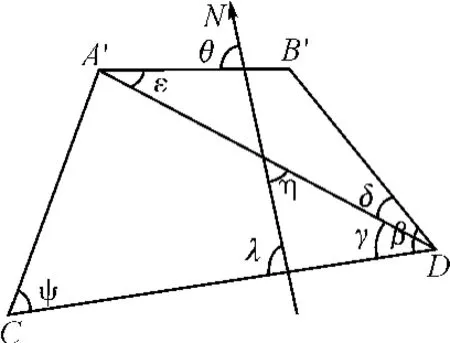
图7 四边形在水平面上的投影
已知A′C、B′D、CD、ψ、β、λ,根据余弦定理有:
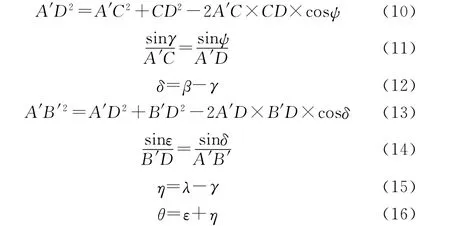
θ即被测基线AB与正北的夹角。
四边形法仅要求A、B两点能够架设反射棱镜,所要求的测量条件较三角形法更容易实现。
4 精度分析
在测量设备基线过程中,三种方法的误差来源主要有平移误差、仪器误差和瞄准误差。三种方法的精度估算如下:
1)方法一的误差来源主要包括平移误差、仪器误差和互瞄瞄准误差。假设在平移过程中,两点在垂直于基线方向上的相对距离误差为2mm,对于长度为4m的基线,其方位角误差约为
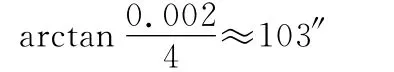
使用差分GPS测量系统,在静态相对差分定位的工作模式下,其相互定位误差为2cm[9],假设差分GPS系统架设距离为100m,则其所确定的参考基线方位角误差约为
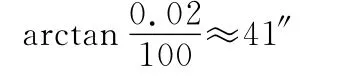
J2级经纬仪一测回水平角中误差为2″,一次互瞄误差最大不超过6″,方位角基准传递计经纬仪两次测量、一次互瞄。则方法一总的测量误差[10]为
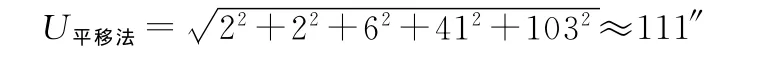
可见,该方法最大的误差源来自于平移误差和差分GPS测量系统的误差,经纬仪瞄准误差和互瞄误差对总误差的贡献极小,可以忽略不计。
2)方法二误差来源主要是仪器误差。由全站仪技术指标可知,对1km的距离,测距误差为0.003m,以0.003m的测距误差计算,两次测距对斜距的最大误差为
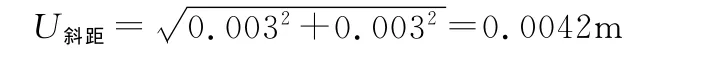
斜距在水平面的投影距离误差应小于与斜距误差,根据安全原则,以斜距误差代替投影距离误差,则由于距离测量误差所引起的基线方位角误差为
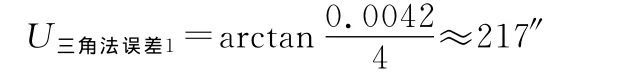
假设差分GPS系统架设距离为100m,则其所确定的参考基线方位角误差为
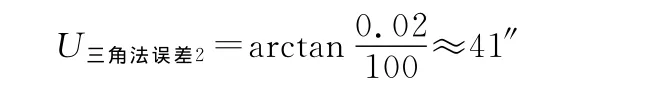
全站仪测量两次仰角和一次水平角对设备基线方位角影响不大于10″。
则方法二的测量总误差为
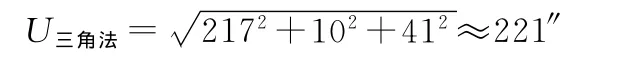
3)方法三误差来源主要为仪器误差,一为全站仪三次的测距误差,全站仪在参考基线CD上的测距误差对设备基线方位角的影响较小,可忽略不计,在AC、BD两方向的测距误差同方法二。二为差分GPS系统的测向误差,误差同方法2,全站仪测量两次仰角和一次水平角对设备基线方位角影响不大于15″,则方法三的测量总误差为
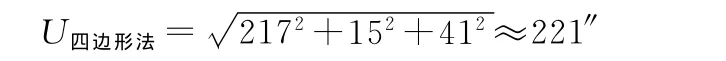
可见方法一的误差主要取决于平移操作所带来的误差;方法二、方法三的测量误差相当,最大误差源均为全站仪测距产生的误差和差分GPS测量系统产生的误差,可适当提高全站仪测距精度和增大差分GPS系统两天线架设距离来减小两种方法的测量误差。
被测基线距离较短是对方位角测量的最大影响,当非通视短基线距离增大时,通过三种方法均可以提高基线方位角的测量精度。
5 结语
本文介绍了测量非通视基线方位角的三种方法,并通过在某型舰卫星设备的实际应用分析了三种方法的精度和对外部条件的依赖程度,可根据被标定设备所需精度和设备周围的环境条件灵活选择。本文介绍的测量方法还可用于非通视基线的长度测量,可广泛应用于隧道、矿山等领域。
[1]许江宁,等.潜艇真航向测量系统[J].中国惯性技术学报,2005,13(3):76-77.
[2]李汉周,等.炮用寻北方位测量系统[J].中国惯性技术学报,2008,16(5):529-530.
[3]张则宇,等.高精度陀螺经纬仪在阵地测量中的应用[J].中国惯性技术学报,2008,16(5):549-551.
[4]段静玄,郑剑飞,赵复政,等.基于全球定位系统的舰载三坐标雷达动态标校方法[J].中国舰船研究,2012,7(4):100-101.
[5]刘高峰,刘健.基于GPS定位系统的舰船雷达标校系统研究[J].舰船科学技术,2006,28(6):100-101.
[6]刘益清,等.用VC实现船舶管子样杆测量中全站仪与微机的通信[J].造船技术,2003(4),28-29.
[7]邹立,孔力.舰载设备互瞄对准方法探讨[J].舰船光学,2002,38(3):21-22.
[8]李维林,李蕾,唐伟方.基于GPS测量系统的舰载作战系统动态航向对准技术研究[J].中国舰船研究,2009,4(4):68-69.
[9]徐绍铨,张华海,杨志强.GPS测量原理及应用[M].武汉:武汉大学出版社,2001:79-89.
[10]沙定国.实用误差理论与数据处理[M].北京:北京理工大学出版社,1993:35-46.
