一种基于GPS的自动航向控制系统＊

2012-10-16董沛然辛爱学

舰船电子工程 2012年12期

董沛然张浩辛爱学王钊

（海军704厂青岛 266109）

1 引言

现代的GPS接收机除了提供位置数据外，还可提供日期、时间、航向和航速等参数［1］，根据这些参数可以对船舶的航路进行规划，实时控制舵角变化以完成自动航向控制。船舶在开阔水域航行时，可以预设好多个航路目标点，本系统即可按照目标点控制船舶自动航行。

2 GPS数据读取

2.1 GPS模块

GPS模块使用GARMIN的12通道GPS15L接收机，同时可以跟踪最多12颗GPS卫星，从而能够快速定位，数据更新率为每秒一次，性能可以满足导航的灵敏度需求和动态需求。数据接口采用异步串行数据输入输出［2］，数据格式使用美国国家海洋电子协会的NMEA 0183ASCII码接口协议［3］。

2.2 GPS数据格式

采用推荐定位信息（Recommended Minimum Specific GPS／TRANSIT Data）格式［4］，该格式定义见表1。

2.3 GPS数据处理

读取GPRMC数据后，分别对第＜3＞项纬度，第＜5＞项经度，第＜7＞项速率，第＜8＞项航向单独读取并存为字符串变量和double型变量，作为下一步流程航向控制的参数［5］。

表1 GPRMC数据格式

3 自动舵控制

航向控制实时更新最新航向变化，从而推算目标航向，在接口单元，建立一个独立线程。该线程完成目标航向计算，目标舵角计算，打舵过程的功能。

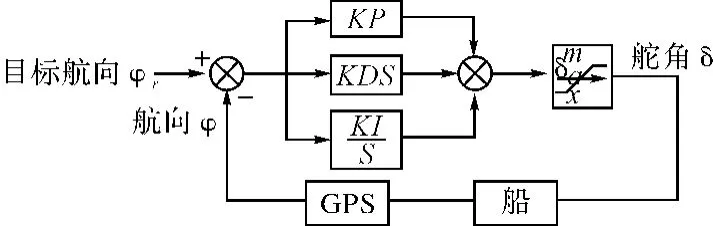
图1 自动舵控制原理

在航向改变过程中，自动舵的舵角并不只是随航向角的偏差而变化，而是和航向差变化的速率以及航向偏差对时间的积分有关［6］。由图1舵角与航向的关系为

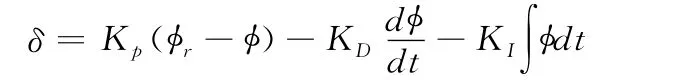
其中K＊＝K·L／μ，T＊＝T·L／μ。

式中L和μ分别是船长和航速，由以上公式可得，当船长，船性能不变Kp与航速平方成反比。

Kd与航速的平方成反比。

若忽略首摇运动的自然频率ωn和阻尼系数ζ，舵角可以简化为

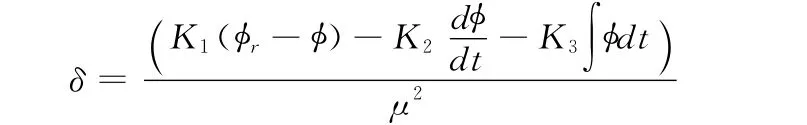
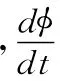
4 航向控制

4.1 目标航向算法

如图2所示，当前航向Dir用实线表示，目标航向Tar用虚线表示，R＿dir指示向右偏转的航向，L＿dir指示向左偏转的航向。

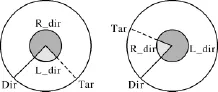
图2 目标航向算法

当Tar＜Dir时候：

所有统计计算均用SASv 9.13统计分析软件进行。定量数据采用t检验、ANOVA或Wilcoxon秩和检验。定性数据用χ2检验、Fisher精确概率、连续校正χ2检验、或Wilcoxon秩和检验，考虑到中心或其他因素的影响采用CMHχ2检验。对于生存数据采用，Log‐rank检验。主要指标的两两比较，采用95%置信区间（95%CI）法，计算双侧95%CI。全部的假设检验均采用双侧检验，取α=0.05。

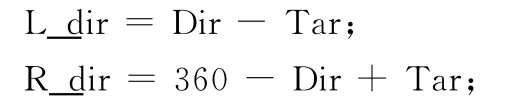
当Tar＞Dir时候：

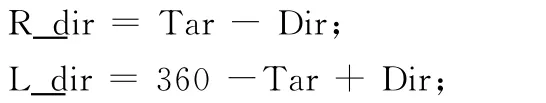
计算完成比较R＿dir及L＿dir大小，判断航向改变的方向和舵角的大小。

4.2 舵角控制优化

当目标航向计算完成，经上述公式得到舵角后，舵角量应经过舵角限定算法，防止舵角超出舵角控制范围。

由于舵机控制及舵的刹车老化，造成了在达到目标舵角时刻断开舵机继电器不能及时停止现象，而且左右舵由于惯性问题冲出的舵角大小不等，所以引入惯性系数概念，读取舵角信息的同时计算舵角变化率，当舵角变化速度高的时候，停舵提前量大，反之，若舵机继电器吸合时间短，舵变化速率慢的情况下，停舵的提前量较小：

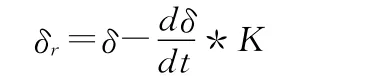
经过一定时间的调试，当K值达到一定的时候，可以使得舵角精度达到±0.3°之间。

4.3 航路规划及执行

能按计划导航点顺序航行，在计算L＿dir、R＿dir前更新目标航向。

程序运行时，依次设置目标点，按顺序记录在内存中，程序装载第一个目标点位置信息，并由当前GPS经纬度计算与目标导航点的航向，更新目标航向，目标航向每秒更新一次，使船按照目标航迹航行。当到达目标点时，程序会自动切换下一目标点，启动新的航向控制［7］。

4.4 航向数据修正

如图4所示，当海浪较大时，会产生大量海浪和船首摇摆等噪音向量，这些噪音向量与真实航向的叠加，航向数据呈正弦型在真实航向周围变化，不能如实反映航向，影响到航向保持功能。

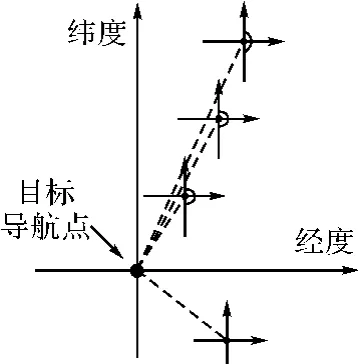
图3 根据当前GPS经纬度计算与目标导航点的航向

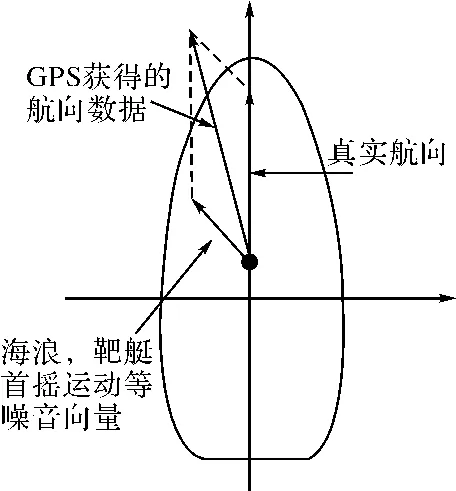
图4 海浪和船首摇摆对航向的影响

c＿PLF1（k）＝［c（k）＋c（k－1）＋ … ＋c（k－FIR＿PLF＿Len＋1）］／FIR＿PLF＿Len

FIR＿PLF＿Len为第一级FIR滤波器长度，即当前时刻输入数据c（k）连同前面（FIR＿PLF＿Len－1）个数据求均值的数据总数。

c＿PLF1（k）为第一级滤波输出；

再用IIR第二级低通滤波平滑：

Delta＿Crt＝c＿PLF1（k）－c＿Avg；Delta＿Crt为当前误差，即最新输入值－上次纪录平滑后取值。

Delta＿Avg＝ Delta＿Crt＊ p＋（1－ p）＊ Delta＿Avg；对误差进行平滑，当前误差Delta＿Crt中含有大量噪声，因此乘p＝0.2，而误差均值Delta＿Avg中可认为已含有较小噪声，因此乘（1－p）＝0.8；

c＿Avg＝c＿Avg＋ Delta＿Avg；经平滑后 Delta＿Avg可以认为含有较小噪声，而真正含有航向角变化需累加到角度中。

滤波流程图如图5所示，经Matlab仿真输出如图6和图7所示。

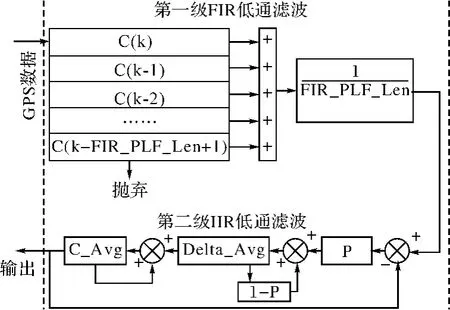
图5 滤波流程图

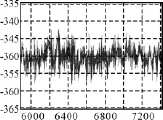
图6 航向仿真图

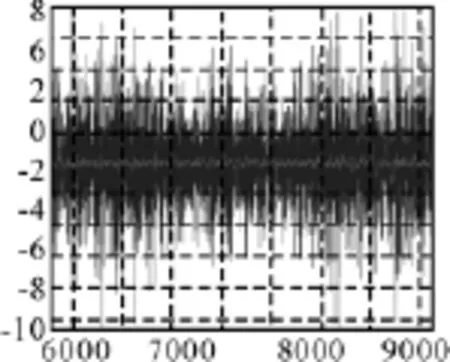
图7 航向差（噪声）仿真

横坐标为时间，单位（s）。波动较大线条为航行数据，波动较小线条是经滤波后的航行数据［8～9］。由图可以看出，真实航行纪录线条很粗，每秒航向差有可能超出10°以上，对程序来说，可能造成这一秒判断打左舵，下一秒判断打右舵，严重影响航向控制参数。数据经过滤波器后，航向差缩减到2°以内，数据平滑，已能符合程序要求。