基于图像匹配的无人机目标定位方法＊

胡海洋 李海林

（海军工程大学电子工程学院 武汉 430033）

1 引言

近年来，无人机在几次高技术局部战争的卓越表现，引起了世界各国的高度重视，许多国家开始大力发展军用无人机技术。为了满足现代信息化战争精确打击的要求，利用无人机侦察图像实现对探测目标的精确定位是其中的关键技术。作为一种特殊的飞行载体，无人机飞行特性复杂、飞行速度较高、成像条件多变，使得具有更为复杂的图像运动特性。而且受天气、光照、噪声等外界因素影响，无人机侦察图像不可避免出现对比度低、模糊甚至遮挡现象［1～2］。为了解决这些问题，从而实现对探测目标的精确定位，需要把无人机图像与具有地理信息的基准图像进行精确匹配。因此，鲁棒性强、实时性好的图像匹配算法成为其中的关键。

由于无人机侦察图像与基准图像不可避免地存在尺度变化、旋转变化和光照变化，而且传统SIFT算法存在耗时长，错匹配多等问题，因此，本文在深入研究SIFT算法的基础上，提出一种基于改进SIFT的图像匹配方法以求达到图像的最佳匹配效果，从而实现对目标的精确定位。

2 图像匹配

所谓图像匹配就是把不同传感器或者同一传感器在不同时间、不同成像条件下对同一景物获取的两幅或多幅图像在空间上进行对准，以确定两幅图像之间的平移以及旋转关系，或根据已知模式到另一幅图像中寻找相应的模式［3］。

如果两幅图像由I1和I2表示，I1（x，y）和I2（x，y）分别表示图像在响应位置（x，y）上的灰度值，那么图像I1和I2的匹配关系可用下面关系式表示：

式中f是几何变换函数，常用的变换模型有：仿射变换、线性等角变换、局部加权平均变换、分段线性变换以及投影变换。

目前，国内外有关专家学者提出了许多图像匹配算法，如基于模板的方法、FFT相关匹配方法、相位相关算法、序贯相似检测算法等，这些匹配算法在某种程度上能够实现图像之间的配准。但是，如果两幅图像之间存在平移、旋转、仿射变换时，算法适应性较差。近年来，局部不变特征对图像旋转、缩放等变化具有较好的适应力，已经成为研究的热点。目前提取点特征比较有名的算子有：Moravec算子、Harris算子、Forstner算子、SUSAN算子等。尤其是1999年Lowe提出的SIFT（Scale Invariant Feature Trans－form）局部特征，它是局部特征研究过程中的里程碑。2005年，Mikolajczyk和Schmid针对不同的场景，对光照变化、图像几何变形、分辨率差异、旋转、模糊和图像压缩等六种情况，对比SIFT、PCA－SIFT、矩不变量、互相关等十种描述子后指出，SIFT描述子性能最好［4］。

3 SIFT特征提取

SIFT特征提取主要包括五个步骤：建立尺度空间；极值点检测；特征点位置精确定位；确定特征点方向；生成SIFT特征描述符［5～8］。

3.1 建立尺度空间

尺度空间理论的目的是模拟图像数据的多尺度特征。高斯卷积核是实现尺度变换的唯一线性核，于是一幅二维图像的尺度空间定义为

然后利用式（2），构造高斯差分尺度空间（DoG scalespace）：

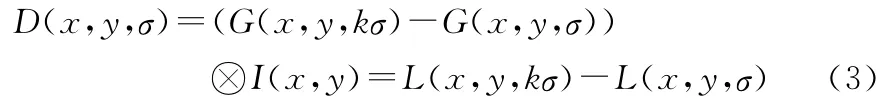
尺度空间的构建过程如图1所示。

图1 构建高斯差分尺度空间

3.2 极值点检测

建立好尺度空间后，传统SIFT算法按照金字塔从第一层至最后一层的顺序对每一个采样点进行与它同尺度和上下相邻尺度的相邻点相比较的操作。如果中间的检测点与它同尺度的8个相邻点和上下相邻尺度对应的9×2个点共26个点比较中是最大或最小，就认为该点是图像在该尺度下的一个极值点。

3.3 特征点位置精确定位

由于DoG检测到的极值点的位置坐标均为整数，而实际的特征点不一定位于整数坐标位置上。因此，在进行极值点遴选之前，先要通过三维二次函数精确定位特征点，再通过计算该位置的DOG响应值及曲率来剔除低对比度的极值点和不稳定的边缘响应点，以此得到真正的稳定极值点，以增强匹配稳定性、提高抗噪声能力。

差分金字塔DoG在候选极值点周围的泰勒展开式如下：

其中，X＝（x，y，σ）T为特征点的位置和尺度信息的向量，X0为候选特征点的位置和尺度信息的向量，D（X0）为该点的差分金字塔DoG值。

3.4 确定特征点方向

利用特征点领域像素的梯度方向分布特性为每个特征点指定方向参数，使算子具备旋转不变性。点坐标为（x，y）处的梯度幅值和方向分别为

在以特征点为中心的领域窗口内采样，并用直方图统计领域像素的梯度方向。梯度直方图的范围是0°～360°，其中每10°一个柱，总共36柱。梯度方向直方图的峰值代表了该特征点处邻域梯度的主方向，即作为该特征点的主方向。当梯度方向直方图中存在主峰值能量80%以上的峰值时，该峰值所对应的方向作为辅方向。特征点可以有一个主方向和多个辅方向，这样可以提高特征匹配的稳定性。

至此，图像的特征点已检测完毕，每个特征点有三个信息：位置、所在尺度、方向。由此可以确定一个SIFT特征区域。

3.5 生成SIFT特征描述符

首先将坐标轴旋转为关键点的方向，以确保旋转不变性。以特征点为中心取16×16的领域作为窗口，将采样点与特征点的相对方向通过高斯加权后归入到8个方向直方图，绘制每个梯度方向的累加值，形成一个种子点。一个特征点由4×4共16个种子点组成，特征描述子由所有子块的梯度方向直方图构成。因此，最终形成128维的SIFT特征向量就是特征描述符。此时SIFT特征向量已经去除了尺度变化、旋转等几何变形因素的影响，再继续将特征向量的长度归一化，则可以进一步去除光照变化的影响。

现有原始图像如图2所示，对其按照上述步骤进行处理，其特征提取结果如图3所示，共检测到2724个特征点，其中箭头方向表示特征点方向，可以发现某些特征点存在多个方向。

图2 原始图

图3 SIFT特征提取结果

4 改进的特征匹配方法

4.1 用准欧式距离代替传统欧式距离

SIFT特征向量的匹配主要就是对两幅待匹配图像的SIFT特征向量进行相似性度量。传统SIFT算法采用比较最近邻特征点和次近邻特征点的欧式距离来判断特征点之间是否匹配。由于SIFT特征向量高达128维，计算量大，程序耗时长，极大影响匹配速度。为了减少运算时间，我们采用文献［9］提出的准欧式距离作为相似度量准则。准欧式距离是准欧式距离矩阵按照水平、垂直、和对象合集分段估计全部的欧式距离，即

由式（7）可知，利用准欧式距离进行两特征向量的相似性度量，只需要一次乘法，而传统欧式距离需要128次乘法和一次开方。因此，准欧式距离能够大大减小计算复杂度，减少匹配时间。

4.2 按照DoG结构由粗至精进行特征匹配

在传统SIFT方法中，按照DoG结构来逐层检测极值点不可避免会出现冗余点或某些特征点同时拥有几个不同特征尺度，从而给后续匹配增加计算复杂度。而图像间基于特征点的匹配，关键问题是确定匹配特征点对的数目。假设图像间存在如下仿射变换：

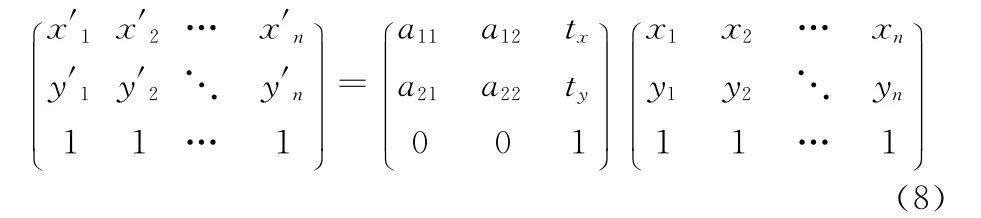
其中｛（x′n，y′n）↔（xn，yn）｜n≥3，n∈N｝是匹配特征点对集合。由式（8）可知，变换矩阵含有6个未知参数，因此若检测到3组不共线的精确匹配特征点对，即可完成图像之间的相互匹配［13］。在实际操作中，为提高匹配精度，可适当增加匹配特征点对数目。

根据上述分析，为了减少特征点匹配时间，考虑匹配过程从金字塔顶层开始，由粗至精进行匹配。如果无人机侦察图像和基准图像正确匹配，能够满足无人机对侦察目标的定位，则停止匹配过程。具体步骤如下：

1）构建侦察图像的高斯差分尺度空间，建立图像金字塔结构；

2）对金字塔顶层图像进行极值点检测，特征点位置精确定位，特征点方向确定和特征描述符生成；

3）将获得的特征点与基准图像的所有特征点进行匹配，并利用RANSAC算法去除错误匹配和估算仿射变换模型后，若获取的匹配对数目达到一定阈值（在这里我们给定经验阈值NThreshold＝40），再根据求取的仿射变换模型进行图像变换以完成匹配，否则，进入金字塔的下一层图像；

4）在新一层图像中，重复2），3）步骤，直至获得足够多的正确特征点匹配对数目，完成匹配。

5 实验结果与分析

为验证本文算法的有效性，检验算法对噪声和场景变化的鲁棒性，针对多幅航拍图像进行了仿真实验。以图2为基准图像，可以看出实验图像4（a）与基准图像存在着尺度变化，实验图像4（b）与基准图像存在旋转变化，实验图像4（c）有大量的噪声，并与基准图像存在光照变化。经过匹配后的实验结果如图5（a）、（b）、（c）所示。实验表明，在场景发生变化和存在噪声的情况下，该方法有效地完成了图像的正确匹配，对噪声和场景变化具有较强的鲁棒性，进而能够实现无人机对侦察目标的精确定位。

从表1可知，该方法在匹配速度上远远优于传统SIFT方法，从而提高了无人机对目标定位的实时性。

图4 实验图像

图5 实验结果

表1 本文算法与传统SIFT耗时对比表（ms）

6 结语

随着科学技术的发展和信息化战争的需求，各种多用途的新型无人机应运而生。相比于卫星等空天侦察平台，无人机的一大优点是能够实时侦察和监视战场，并能及时将战场信息以图像方式传输给指挥中心。利用无人机侦察图像实现对目标的精确定位，需要把无人机图像与具有地理信息的基准图像（比如卫星图像）进行正确匹配。由于SIFT特征是图像的局部特征，其对旋转、尺度缩放、亮度变化保持不变性，本文提出一种基于改进SIFT的图像快速匹配方法。实验表明，该方法可以实现图像之间的正确匹配，有利于无人机对探测目标的精确定位，并且具有较好的实时性。

［1］程远航.无人机航空遥感图像动态拼接技术的研究［D］.辽宁：东北大学，2008：3－5.

［2］杨涛，张艳宁，张秀伟，等.基于场景复杂度与不变特征的航拍视频实时配准算法［J］.电子学报，2010，38（5）：1070－1076.

［3］吴雅娟，陈尧，尚福华.一种新的基于相似度计算的本体映射算法［J］.计算机应用研究，2009，26（3）：870－872.

［4］王永明，王贵锦.图像局部不变性特征与描述［M］.北京：国防工业出版社，2010，4.

［5］Mikolajczyk K，Schmid C.A performance evaluation of local descriptors［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2005，27（10）：1615－1630.

［6］Lowe D G.Object recognition from local scale－invariant features［C］／／Proceedings of the ICCV，Kerkyra，Greece，1999：1150－1157.

［7］Tomasi C，Kanade T.Detection and tracking of point features［R］.Camegie Mellon University，Technical Report，1991：1－20.

［8］Lindberg T，Scale－space theory：a basic tool for analyzing structures at different scales［J］.Journal of Applied Statistics，1994，21（2）：224－270.

［9］程德志，李言俊，余瑞星.基于改进SIFT算法的图像匹配方法［J］.计算机仿真，2011，28（7）：285－288.

［10］李山飞，龚俊斌，李斌，等.基于实时地形校正的InSAR图像匹配算法［J］.计算机与数字工程，2012（1）.

［11］杜振鹏，李德华.基于KD－Tree搜索和SURF特征的图像匹配算法研究［J］.计算机与数字工程，2012（2）.

［12］李竹林，常艳梅.一种基于Hausdorff距离的图像匹配算法［J］.计算机与数字工程，2012（6）.

［13］张书真，宋海龙，向晓燕，等.采用快速SIFT算法实现目标识别［J］.计算机系统应用，2010，19（6）：82－85.