空时编码OFDM与多维波束形成组合算法研究＊

（公安海警学院电子技术系 宁波 315801）

1 引言

空时编码是一种能获得发射分集和编码增益的有效手段，其应用范围已经从平坦衰落的MIMO系统推广到MIMO－OFDM系统［1～6］。近年来，如何在已知全部或部分信道信息的前提下设计发射方案已经引起了学者们的广泛兴趣，这些工作主要集中在平坦衰落的 MIMO系统［7～9］，对于MIMO－OFDM系统的研究相对较少，文献［10～11］中作者假设发射端完全已知瞬时信道信息，对波束形成进行最优化设计，由于MIMO－OFDM系统需要在各个子载波上分别进行波束形成设计，这需要很大的信道反馈信息量，另外假设接收端精确已知全部的信道信息在无线通信环境下不太现实；为了减少反馈信息量，文献［12］中 MIMO－OFDM系统的接收端只返回部分波束矢量信息，在发射端采用插值的方式重构所需的波束矢量。另外，联合采用波束形成和空时编码能在保持空时编码所带来增益的同时充分利用发射端已知信道信息来提高系统性能，特别当采用空时分组编码时，系统接收端可以进行快速的最大似然检测。文献［13］提出了一种基于平均反馈模型的自适应两维空时编码波束形成方案，它对空时分组编码和波束形成进行了联合设计，并对信道信息的反馈误差具有一定的健壮性。

本文的方案在空时分组编码的选取上并不依赖于实际发射天线数，因此可以在分集度、编码增益以及系统码率之间进行灵活的折中。同时还发现，当实际发射天线数大于空时分组码所需天线数时，系统的编码增益会随着实际发射天线数的增加近似呈线性增长，并且其增长速度随着发射天线阵列间相关性的增强而增大。另外，由于不同子载波上有相同的优化问题，本文提出的方案具有设计简单的优点。

2 系统模型

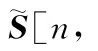
其中H［n，k］表示第n个OFDM空时码块中第k个子载波上的信道频率响应矩阵，矩阵元素Hij［n，k］具体表示为

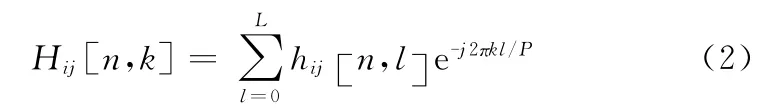
hij［n，l］为发射天线j到接收天线i之间信道在l条径上的时域冲击响应，不失一般性我们约束E［］＝1／（L＋1）；V［n，k］表示噪声矩阵，其元素为统计独立的零均值单维方差N0／2的复高斯白噪声。

3 波束形成及性能分析

3.1 波束形成矩阵优化问题

在发射端已知MIMO信道的空间相关统计特性，通过优化波束形成矩阵使发射信号“适应”信道的相关特性，这里主要用最小化误码率（SER，symbol error rate）求解上述优化问题。假设在接收端已知信道信息（CSI，channel state information）并采用最大似然解码时，当实际发送信号是S［n，k］而解码为S′［n，k］的错误概率为［4］

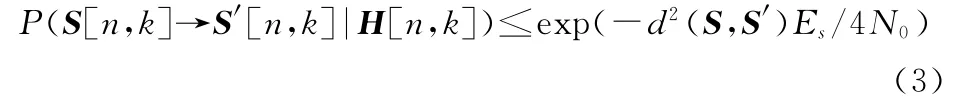
其中Es为码元的平均能量

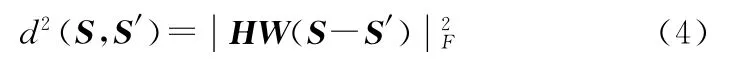
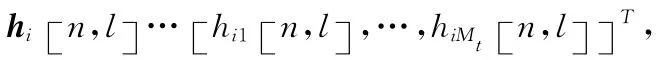
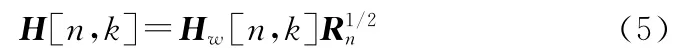
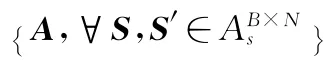
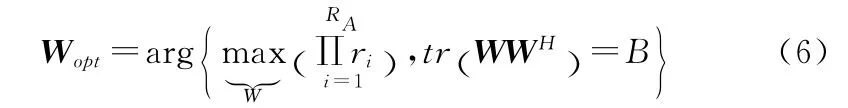
首先假设Rank［R1／2］＝B，并以此为基础进一步分析Rank［R1／2］≠B 的情况。此时对矩阵R1／2进行特征分解可得

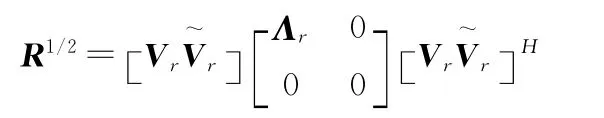
利用Hadamard不等式有

并且当Φ为对角阵时上述不等式中的等号成立。令Φ＝diag（ φ1，φ2，…，φB），此时

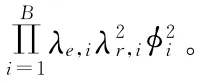
其中λe，i，λr，i分别为Λe，Λr的第i个对角元素。上述分析假设 Rank［R1／2］＝B，在Rank［R1／2］≠B 的情况下实际上只要选择相关矩阵R最强的B个特征向量组成Vr，观察式（7）可知任意其他的选择必然得到一个相对较小的J值。由此可见，最优的多维波束形成需要同时“适应”信道的空间相关性以及空时编码特性。当选择正交空时编码，即EEH＝ρI，ρ为常数，则Ve＝I，Wopt＝Vr，此时多维波束选择R最强的几个相互正交的特征向量。

3.2 编码增益性能

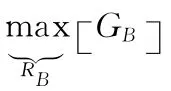
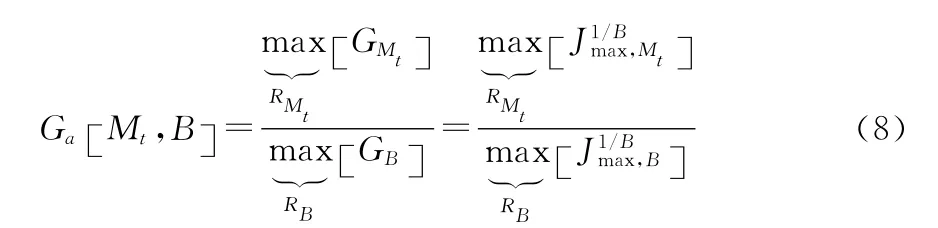
把式（7）代入上式可得

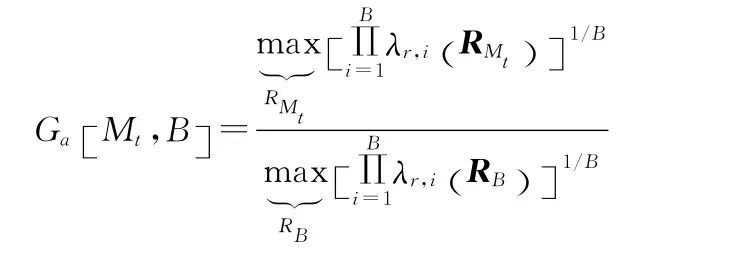
4 仿真结果

本节用计算机仿真来进一步验证本文提出系统的性能，信道可分辨多径数取为4，即L＋1＝4；OFDM载波数选为P＝64；在仿真本文所提方案时皆采用2×2的Alamouti空时编码方案［2］以及QPSK调制方式。为了考察文中提出的系统方案在不同配置参数下的误码性能以及信道相关性对系统性能的影响，分别仿真了具有不同天线配置的系统性能。假设天线布置采用均匀线性阵列并且相邻天线之间距离为d，接收端信道之间互不相关，而发射端信道存在相关性，各天线之间的相关性可以采用文献［14］中的信道模型，它主要由天线之间的距离以及无线环境中发射端散射簇的平均出射角、出射角的均方根三个参数决定。计算机仿真时采用了两种具有不同空间相关性强度的信道模型，即相邻发射天线之间的相关性分别为｛ρ1＝0.8，ρ2＝0.8，ρ3＝0.7，ρ4＝0.7｝和｛ρ1＝0.4，ρ2＝0.4，ρ3＝0.3，ρ4＝0.3｝，ρ的下标表示各可分辨径。

图1 强相关性道模型下的系统性能曲线

图1示意了在强空间相关性信道模型下不同天线配置时系统不同发射方案的误比特率性能曲线。由图可见，本文提出的空时编码和波束形成组合方案的性能相比STBC OFDM方案而言具有明显的性能增益，当采用4根发射天线时，系统性能有3～4dB的增益；当采用6根发射天线时，系统有5～6dB的增益。图中还给出了4发2收天线配置下空时编码和传统的波束形成组合方案（STBC Conv.Beam）以及文献［13］中发 射 方 案（STBC4 Beam）的性能曲线，以便进一步比较。所谓传统的波束形成方案这里指的是把多维波束形成矩阵W的第一维波束方向取为相关矩阵R对应最大特征值的特征矢量，而其余各维都取为零。结果表明，采用传统的波束形成方案会损失系统的发射分集度。一般意义上来说，传统的波束形成方案能获得最大的阵列增益，而图1性能曲线表明，采用同样的天线配置，结合相同的空时编码方案，本文提出的波束形成方案相比传统的波束形成方案在误码性能上有明显的优势，即使在很低信噪比情况下也是性能相当。当采用文献［13］中的发射方案，由于此时采用了速率为0.5的4维的空时编码，它具有更高的发射分集度。为了和本文方案在同等速率条件下进行性能比较，该方案采用16QAM调制方式。结果表明，在同样的天线配置下，本文提出的方案比STBC4Beam方案具有明显的性能优势，在低信噪比时有2dB左右的增益，随着信噪比的增加增益逐渐缩小，这是由于STBC4Beam方案采用了更高维的空时分组码而具有更高分集度的缘故。

图2 弱相关性道模型下的系统性能曲线

图2给出了弱空间相关性信道模型下不同天线配置时系统的性能曲线，所得的结果基本和图1类似，不同的是，该信道环境下通过增加发射天线数所获得的性能增益相对较小，这是由于系统可获编码增益的大小和天线阵列的相关性密切相关，总体上来说，天线阵列相关性越强，可获编码增益越大。另外，此时STBC4Beam方案在高信噪比时性能优于本文的方案，说明在弱空间相关性信道环境下，提高系统的分集度相比编码增益更占优势，而本文提出的方案在较强相关性信道环境下则具有更高的效率。

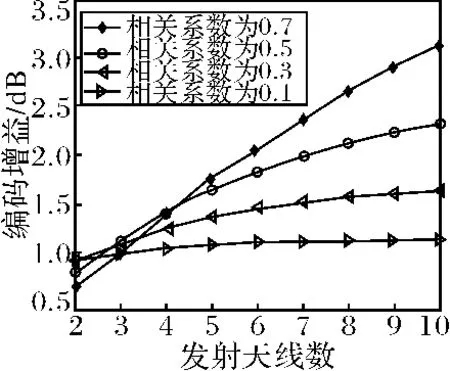
图3 系统编码增益随发射天线数的变化曲线

为了进一步考察不同信道环境下天线增益的情况，给出了编码增益随发射天线数的变化曲线，如图3所示，这里的编码增益G如3.2节所定义。结果表明，在不同的信道环境下编码增益都随着发射天线数的增加而增加，并近似呈线性增长趋势。当信道相关性很弱（信道相关系数为0.1）时，系统编码增益随天线数增长的速率很低，图中表现为曲线很平坦。随着信道相关性的增强，系统编码增益随天线数增长的速率也随着提高，如图所示，当信道相关系数为0.7时，增益曲线基本上为直线，且具有较大的斜率。上述结果表明，在信道存在较强相关性时，采用本文提出的组合方案，同时配置比期望的分集度更多的发射天线，可以获得明显的编码增益从而提高系统的总体性能。

5 结语

为了在发射端充分利用信道的统计信息，本文提出了一种空时编码OFDM结合多维波束形成的方案，理论分析表明该方案能获得最大的发射分集度以及编码增益，并具有设计灵活、简单有效等优点，当增加实际发射天线数时系统的编码增益能得到准线性的提高，同时保持空时编码的发射分集度。信道环境相关性越强时，通过增加实际发射天线数所获得的编码增益的增长率越高。仿真结果亦证实了上述结论，尤其当发射天线数大于期望分集度时，多维波束形成能大大提高系统的误码性能。

［1］FOSCHINI G J，GANS M J.On the limits of wireless communications in a fading environment when using multiple antennas［J］.Wireless Personal Commun，1998，6（3）：315－335.

［2］ALAMOUTI S M.A simple transmit diversity technique for wireless communications［J］.IEEE J Select Areas Commun，1998，16（8）：1451－1458.

［3］TAROKH V，SESHADRI N，CALDERBANK A R.Space－time codes for high data rate wireless communication：performance criterion and code construction［J］.IEEE Trans Inform Theory，1998，44（2）：744－765.

［4］TAROKH V，SESHADRI N，CALDERBANK A R.Space－time codes for high data rate wireless communication：performance criterion and code construction［J］.IEEE Trans Inform Theory，2002，44（2）：744－764.

［5］AGRAWAL D，TAROKH V，NAGUIB A，et al.Space－time coded OFDM for high data－rate wireless communication over wideband channels［J］.Proc IEEE VTC，2007，3：2232－2236.

［6］LEE K F，WILLIAMS D B.A Space－frequency transmitter diversity technique for OFDM systems［C］／／Proc IEEE GLOBECOM，2008.1473－1477.

［7］VISOTSKY E，MADHOW U.Space－time transmit precoding with imperfect feedback［J］.IEEE Trans Inform Theory，2009，47（6）：2632－2639.

［8］SAMPATH H，PAULRAJ A.Linear precoding for space－time coded systems with known fading correlations［J］.IEEE Commun Letters，2008，6（6）：239－241.

［9］ZHOU S L，GIANNAKIS G B.Optimal transmitter eigenbeamforming and space－time block coding based on channel correlations［J］.IEEE Trans Inform Theory，2011，49（7）：1673－1690.

［10］PASCUAL I A，PEREZ－NEIRA A I，Lagunas Hernandez M A.Joint beamforming strategies in OFDM－MIMO systems［C］／／Proc IEEE ICASSP，2010.2845－2848.

［11］AKAY E，SENGUL E，AYANOGLU E.Performance analysis of beamforming for MIMO OFDM with BICM ［C］／／Proc IEEE ICC，2010.613－617.

［12］CHOI J，HEATH R W.Interpolation based transmit beamforming for MIMO－OFDM with limited feedback［J］.IEEE Trans Signal Processing，2005，53（1）：4125－4135.

［13］XIA P F，ZHOU S L，GINANAKIS G B.Adaptive MIMOOFDM based on partial channel state information［J］.IEEE Trans Signal Processing，2004，52（1）：202－213.

［14］马一森，李智，赵建华，等.OFDM通信系统的分析及其Simulink仿真研究［J］.计算机与数字工程，2010（11）.

［15］何飞，蒋冬初，赵政春.基于 MIMO－OFDM系统的信道估计方法分析［J］.计算机与数字工程，2010（1）.

［16］王争艳，武林俊.超宽带OFDM系统中比特与功率分配算法研究［J］.计算机与数字工程，2011（7）.

［17］SADEK A K，SU W F，RAY LIU K J.Eigen－selection approach for joint beamforming and space－frequency coding in MIMO－OFDM systems with spatial correaltion feedback［C］／／IEEE Workshop on Signal Processing Advances in Wireless Commun，2011：565－569.