空中高速路突发事件消散建模

张兆宁，黄雪征，王莉莉

(中国民航大学空中交通管理学院，天津300300)

0 前言

为了适应下一代空中交通运输系统，需要开拓新的空域结构去适应未来航空器需求的增长，所以一种具有发展潜力的空域结构——空中高速路被提到了日程。空中高速路与地面高速路具有很大的相似性，例如，移动单元速度都很大，都具有跟驰特性及都可以看成连续流来处理等。

因为恶劣天气原因造成的航路拥堵的问题比较突出，航路拥堵可以造成航班延误［1］，管制员为了改善航路拥堵问题采取的措施一般都是盲目的采用地面等待的方法，而从来没有考虑航路拥堵的传播规律，只有了解了航路拥堵的形成与消散过程，对症下药，才能达到更好的管制效果。

元胞传输模型在处理地面交通事件的拥堵问题上得到了广泛的应用，例如:文献［2］建立了地面快速路突发事件的元胞传输模型，有效地减少了交通延误;文献［3］将元胞传输模型运用到空中交通流控制的应用中，证实了该模型在空中流量的建模中也是适用的。本文利用空中高速路与地面高速路的相似性，针对航路拥堵问题，将地面元胞传输模型(CTM模型)［4］改进并运用到空中高速路，描述空中高速路上遇到突发事件时，航路拥堵的形成及消散过程，为管制员的管制活动提供理论依据。

1 空中高速路的CTM模型

基本思想:假设一条单向无交叉的航路，只有一个进口和一个出口［5-6］。将该航路平均分成等距离的间隔，每一小段的长度等于飞机自由流速度在一个单位时间内行驶的距离。把每一小段称为一个单元［7-8］。在交通量很小的时候，一个单元内的航空器在一个单位时间内可以完全驶入相邻的下一单元。空中元胞传输模型如图1所示。

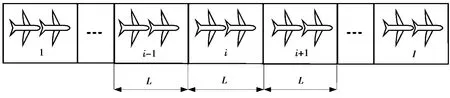
图1 空中元胞传输模型

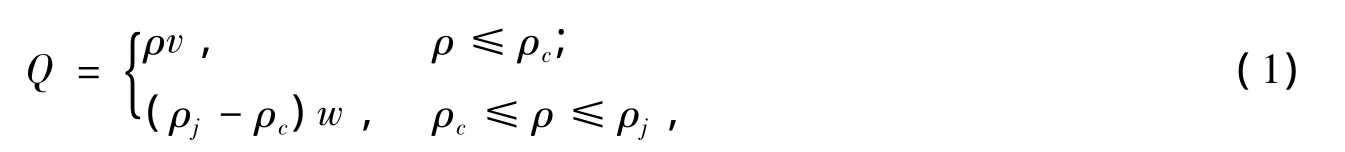
CTM模型将交通流中密度与流量的二次函数关系图简化近似为一次的线性关系。式中，v为自由流速度;w为拥挤波向后传播的扰动;ρj是拥塞密度;Qmax是通行能力。为了说明方便引入下列符号

Ri(t):i元胞最大允许容纳的飞机数;

Qi(t):i元胞的通行能力(i－1元胞和i元胞通行能力的最小值);

fi(t):t时间段内，通过i元胞的实际流量;

ri(t):t时间段内，i元胞的实际飞机数。

CTM模型中各参数随时间的变化可以用下列式子表示

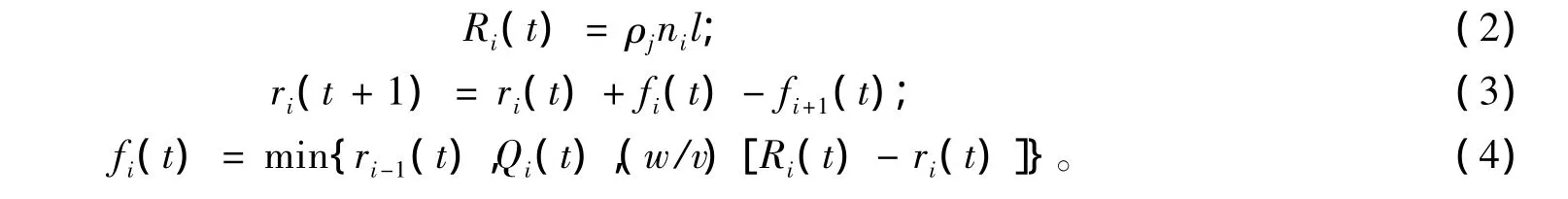
式(2)表示元胞i的最大容量，等于拥塞密度、航道数和元胞长度三者的乘积。式(3)表示t+1时刻元胞i的实际容量，等于t时刻元胞i的容量加上流入i元胞的流量再减去流出i元胞的流量。式(2)～式(4)可以用图2形象表示。

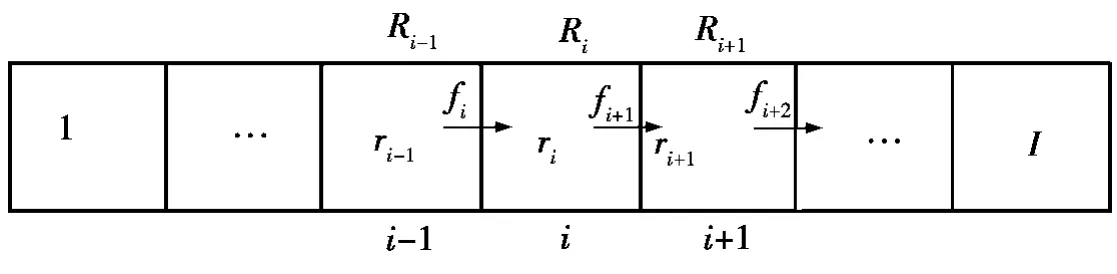
图2 R，r，f关系图

2 突发事件形成和消散持续时间建模

CTM模型中各参数都是随时间变化的［9］，所以通过改变各参数的值，可以很好地描述具体航路模型在突发事件下拥塞的形成和消散过程。建立如图3所示的一条单向无匝口的空中高速航路。

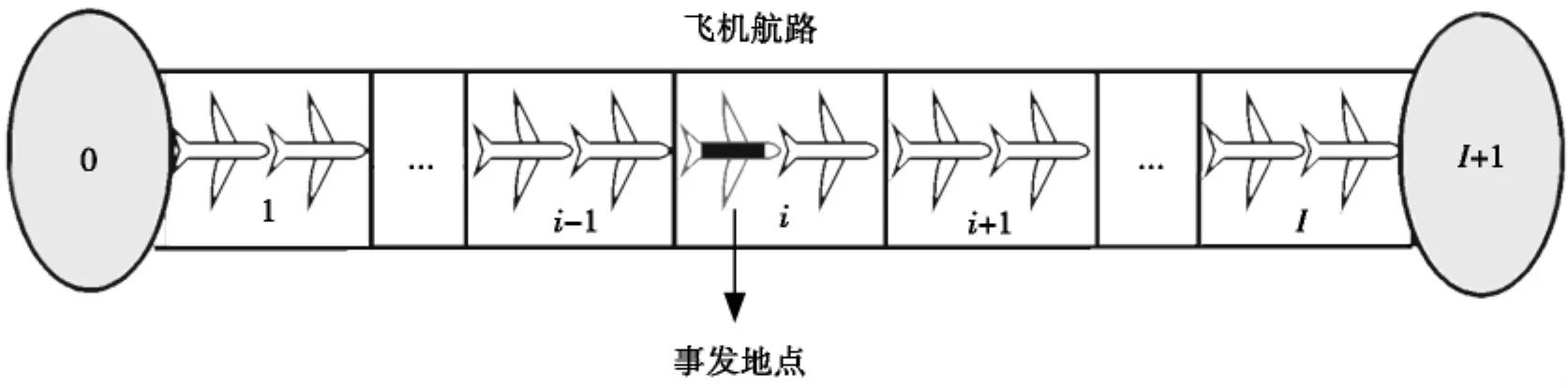
图3 突发事件下的CTM模型

在航路的两端各有一个元胞，假设为0元胞和I+1元胞，0元胞内存储着要进入航路的所有交通容量，I+1元胞表示飞出该航段的航空器能被I+1元胞完全吸收。1元胞内的通行能力Q1(t)满足动态交通需求D(t)。如下式表示式中，r0(1)表示0元胞在t=1时段的存储量;Q1(t)表示在t时刻元胞1的通行能力;D(t)表示t时刻起航路的外部需求。当发生突发事件以后，密度流量关系图中会下降，ρj和w也会发生相应的变化。

当i元胞发生突发事件时，该元胞的Qi(t)、Ri(t)、Wi(t)都会发生相应的变化，假设变为否则为 Qi、Ri、Wi。

3 仿真结果及分析

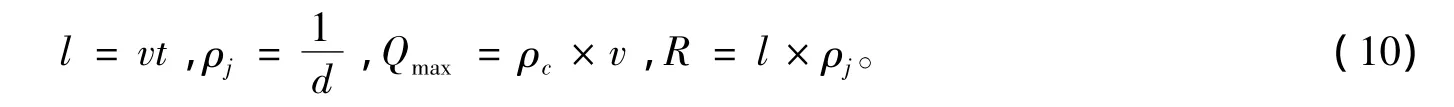
一条北京到广州的空中高速路长1 920 km，以运行航空器自由流速度800 km/h为例，单位时间取12 min，最小安全间隔取5 km。每个元胞的长度为160 km，航路可以分为12个元胞单元，某一时刻在1 600 km(第10个元胞单元)处发生突发事件，事件持续了1.2 h，通行能力下降到50%。通过式(10)，可以得到=16，N=32=8，将交通流数据用Matlab进行仿真分析得到两种管制方式的仿真图，如图4所示。

根据民航局安全飞行相关规定，飞行器空中飞行允许的巡航速度范围为650 km/h≤v≤900 km/h，最小安全间隔范围是5 km＜d≤10 km。选取速度范围内的某一速度v为自由流速度，取安全间隔范围内的d为安全间隔。事件持续事件为t，可以得到如下参数

图4 飞行器飞行管制仿真对比图

图4 a表示在该航路中飞机按均匀的流量15架在里面运行，在发生突发事件后，管制员没有对进入该航路的飞机流量进行管制，还是按照原有的交通量让其进入航路。随着事件时间的延续，在事件发生地点的上游区域形成拥堵区域，并且随着事件持续时间的增长，交通拥挤一致往交通流的上游推移，可以看出在事件持续1.2 h的情况下，拥挤波传递到了第7个元胞单元，第3个时间步长时刻事发地点所在元胞内飞机数达到了24架，而事发地点下游的元胞内由于拥堵飞机的数量开始减小，随着事件的持续将一致向下游扩散。在事件被清除后，拥挤部分范围慢慢向下游传递并逐渐消失，可以看出消散的时间比事件持续的时间长，为1.6 h。图4b表示在突发事件发生时，管制员对其进行合理管制的情况下，在事件持续相同时间的情况下，消散时间为0.6 h。从图4中可以看出:通过管制活动突发事件的拥堵消散时间占未管制情况下拥堵消散时间的64.0%;消散时间占37.5%。从以上数据可以看出:通过管制活动，大大提高了突发事件情况下拥堵的消散效率。从图4b中可以直观形象的看出通过管制活动整个事件的消散过程，所以通过该模型模拟不同流量进入航路情况下，突发事件的拥挤消散过程，可以给管制员的管制活动提供很好的依据。

4 结论

通过元胞传输模型模拟空中高速路突发事件的形成和消散过程，可以为管制员的管制活动提供依据。管制员可以根据事件的性质，事件的持续时间以及事件发生前流量的大小来决定应该采取何种管制活动，从而增加空域的使用效率以及提高航班的运行效率。

［1］褚芳芳.气象信息不确定下的地面等待模型在ATFM中的应用［D］.西安:西北工业大学，2007.

［2］姬杨蓓蓓，张小宁，孙立军.基于元胞传输模型的交通事件消散建模［J］.重庆交通大学学报，2008，27(3):442-445.

［3］刘强，白存儒，林键，等.空中交通流线性二次型最优控制［J］.交通与计算机，2008，26(6):116-119.

［4］杨晓光，彭春露，刘好德，等.城市道路上救援车辆行程时间可靠性仿真研究［J］.交通与运输，2006(z2):45-49.

［5］王秋平，王中芳，赵硕.动态交通流分配模型［J］.长安大学学报，2011，31(2):81-85.

［6］张毅华，陈森发.紧急事件下疏散元胞传输宏观模型研究［J］.公路交通科技，2010，27(2):110-114.

［7］刘小明，胡红.应急交通疏散研究现状与展望［J］.交通运输工程学报，2008，8(3):108-117.

［8］Sun D F，Alexandre M B.Multicommodity Eulerian-Lagrangian Large-Capacity Cell Transmission Model for En Route Traffic［J］.Journal of Guidance，Control，and Dynamics，2008，31(3):616-628.

［9］Sun D F.Comparison of the Performance of Four Eulerian Network Flow Models for Strategic Air Traffic Management［J］.Networks and Heterogeneous Media，2007，2(4):569-595.