基于自动微分技术的多平衡机状态估计算法

叶 芳，卫志农，孙国强，王 超

(1.河海大学能源与电气学院，江苏南京 210098;2.浙江电力调度通信中心，浙江杭州 310007)

EMS中许多高级应用软件都以可靠的电网数据为基础.电力系统状态估计[1-5]能够基于电网结构、参数以及实时量测，为EMS提供精度高、完整而可靠的电网数据，因此，电力系统状态估计的精度将影响EMS的实用化水平.电力系统传统的状态估计通常只选择1台具有较大调节余量的发电机作为平衡机，按照单平衡机的设置进行程序开发和计算分析.但是随着电力系统规模的逐步增大，单平衡机已经难以满足系统功率平衡的要求，因此目前各省电网大多数设置1组平衡机，这样势必给传统的状态估计程序带来新的挑战.如果可以根据电力系统的实际情况引入多平衡机的思想，那么状态估计的结果必然会更接近实际状态，从而为EMS的后续分析.如静态安全、电压稳定等分析，以及采用相应的保护控制措施提供重要的数据支持.目前多平衡机在电力系统潮流计算中的应用已得到了广泛的关注[6-10]，但在电力系统状态估计中的应用还较鲜见.

自动微分(automatic differentiation，AD)技术[11-12]是计算机数值计算和分析领域内一项崭新的技术，与其他微分方法(如除法微分、符号微分)不同，它将微分定义为代数运算，基于链式法则自动计算函数的任意阶导数，且无论采用正模式还是逆模式[13]，均避免了截断误差.特别是在获得雅可比矩阵上，AD技术具有很大的优势.文献[14-17]分别将AD技术应用于电力系统潮流计算、最优潮流以及灵敏度分析，表明AD技术在电力系统中的应用是可行、优越的.

笔者在经典加权最小二乘法的基础上，将多平衡机的影响计入状态估计模型中，通过基于运算符重载的ADOL-C[18]工具获得量测函数的雅可比矩阵，实现了求导的自动化.IEEE14，IEEE30，IEEE57，IEEE118节点测试系统的仿真结果验证了所提算法的有效性.

1 计及多平衡机的状态估计模型

计算机已经成为现代电力系统调度中心很重要的部分，保证计算机在线应用水平的关键是数据库的质量，而由远动装置传送过来的实时数据，由于远动装置本身的误差以及传送过程中各个环节造成的误差，导致存在不同程度的精度和可靠性问题.电力系统状态估计的功能相当于滤波，利用实时量测系统的冗余度来提高数据精度，自动排除随机干扰所引起的错误信息，估计系统的运行状态.

状态估计的已知条件是电力系统的实时量测z，一般是节点电压幅值、节点注入或支路的有功功率和无功功率.设系统有n个节点，有

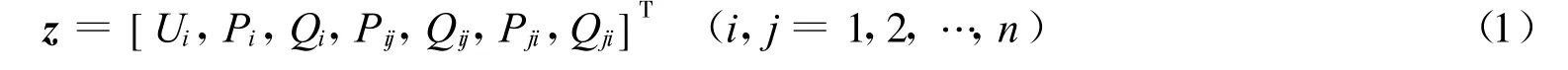
式中:Ui——第 i个节点的电压幅值;Pi，Qi——第 i个节点的注入有功功率、无功功率;Pij，Qij，Pji，Qji——支路i-j的首、末端有功功率和无功功率.

状态估计的未知条件即状态量x一般为节点电压的实部和虚部，假设系统有m+1个平衡节点(具有较大调节余量的发电机节点)，则 x=[e1，f1，…，en-m-1，fn-m-1]T.

由于量测量数l大于状态量数2(n-m-1)，以及量测误差的存在，不可能找到一个，使得残差矢量r()=z-h()各分量均为0，但可以找到一个，使得加权残差平方和为最小，为此，建立目标函数

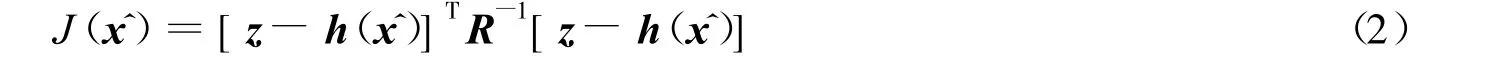
式中:h——由基尔霍夫定律、功率平衡等基本电路定律所建立的量测函数;R——以σ2i(i=1，2，…，l)为对角元素的量测误差方差阵，R-1起权重的作用.

经典加权最小二乘状态估计就是求使目标函数达到最小时x的值，对 h进行线性化假设，即对h进行泰勒级数展开并忽略二次以上非线性项，可以得到

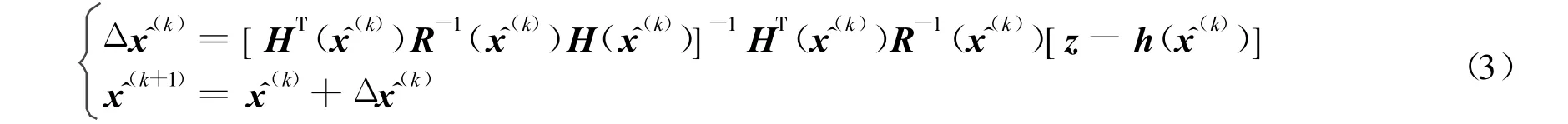
其中

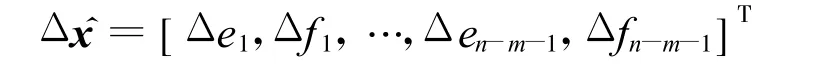
2 AD技术

2.1 基本原理

运用计算机进行目标优化、灵敏度分析、大规模数值模拟等已成为各领域学者广泛关注的问题，微分运算是这些热点课题的基本运算之一.目前利用计算机生成函数微分代码的方法主要有4种[13]:常规方法、除法微分、符号微分和自动微分.常规方法就是先推导出导数的解析表达式，然后再编制计算机程序.该方法很容易得到效率最高的代码，在状态估计中经常被使用.除法微分可以得到函数在某个特殊点处的微分，但得到的是微分的近似，精度很难估计.符号微分具有操作代数表达式的功能，但通常不能处理如分支、循环或子程序这样的计算机代码，应用中受到限制.

无论函数多么复杂，总是由一系列基本元函数(如sin，cos，exp等)和四则运算符(+，-，×，÷)经过有限次组合而成.AD技术基于该事实，根据微分计算的链式法则，不需要推导导数计算公式就可以自动计算函数的微分，且不含截断误差.

ADOL-C[18]是由Dresden技术大学科学计算学院开发的自动微分系统，利用C++高级语言中操作符重载的机理，通过重载每个操作以达到计算偏导数和根据链式法则传递导数的目的，而且能够以正模式和逆模式计算任意阶导数.基于以量上优点，笔者选择ADOL-C工具进行微分计算

2.2 AD技术在多平衡机状态估计中的应用

由式(3)可知，在多平衡机状态估计中，需要求取量测函数的雅可比矩阵H.常规方法在已知量测函数表达式的基础上，先推导出H各元素的解析表达式，然后根据具体的表达式编写计算机代码.该方法繁琐且容易出错，且随着电力系统结构越来越复杂，如果采用常规方法进行软件更新，不仅需要修改量测函数的代码，更繁杂的是要修改相应的雅可比矩阵的代码，这必然导致更新速度慢、难度大等问题.

AD技术能够直接根据量测函数表达式，通过微分计算的链式法则，在正模式和逆模式下自动生成 H.在软件更新的过程中只需要修改量测函数的代码，因此可以大幅度降低工作量，提高更新速度.

以支路1-2上的始端有功功率量测P12为例，说明AD技术分别在正模式和逆模式下计算函数微分的原理.P12的解析表达式为

式中:g——支路电导;b——支路电纳.

引入独立变量 x1～x4和中间变量 x5～x14，将P12分解成一系列基本运算:独立变量 x1=e1，x2=f1，x3=e2，x4=f2;中间变量 x5=，x6=，x7=x1x3，x8=x2x4，x9=x1x4，x10=x3x2，x11=(x5+x6)g ，x12=(x7+x8)g，x13=(x9-x10)b，x14=x11-x12，P12=x14+x13.在已知独立变量值之后，自顶而下就可以得到 P12的精确值.

2.2.1 运用正模式进行求解

通过微分计算的链式法则，自顶而下就可以求得d P12:

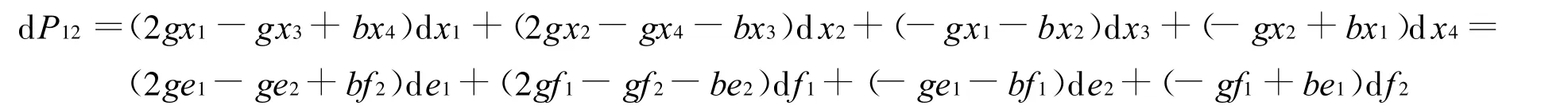
从而得到

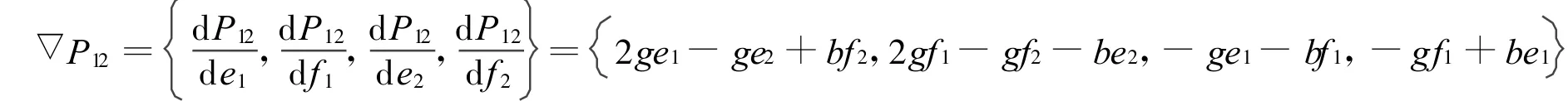
2.2.2 运用逆模式进行求解

令 d xi=0(i=1 ，2，…，14)，有

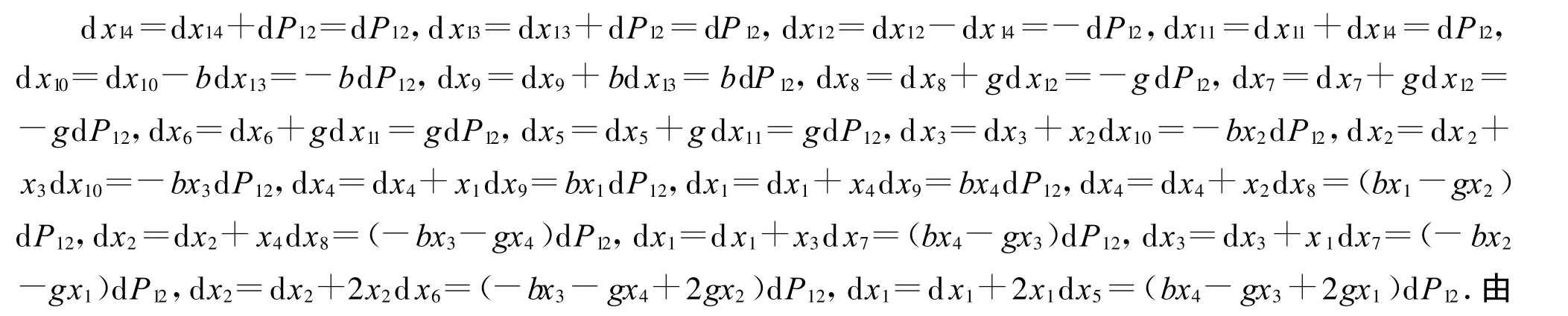
此得到

算法的流程如图1所示.

3 算例分析

分别对IEEE14节点、IEEE30节点、IEEE57节点和IEEE 118节点的标准算例进行仿真计算，算例数据见表1.仿真中，在潮流计算结果的基础上叠加相应的随机量测误差形成量测数据，以潮流计算得到的电压模拟平衡节点电压.

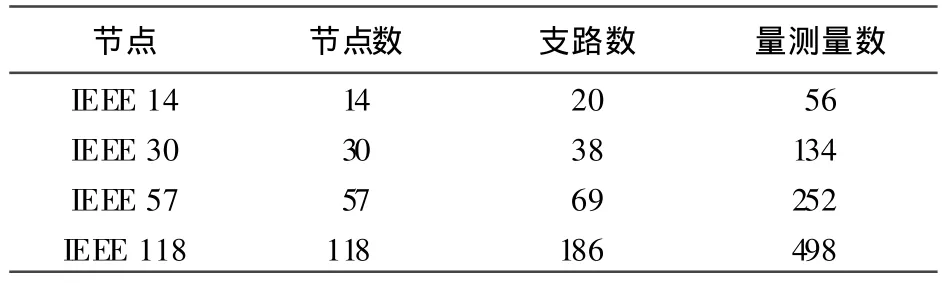
表1 IEEE算例数据Table 1 Data of IEEE test systems

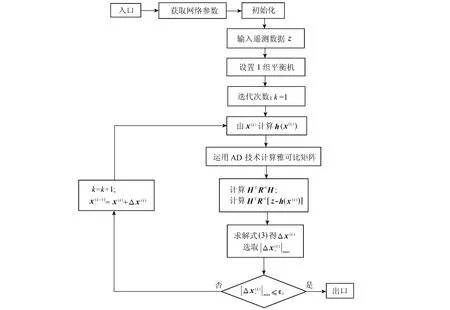
图1 运用AD技术的多平衡机状态估计算法程序框图Fig.1 Flowchart of state estimation algorithm for multi-balancing machines with AD technology

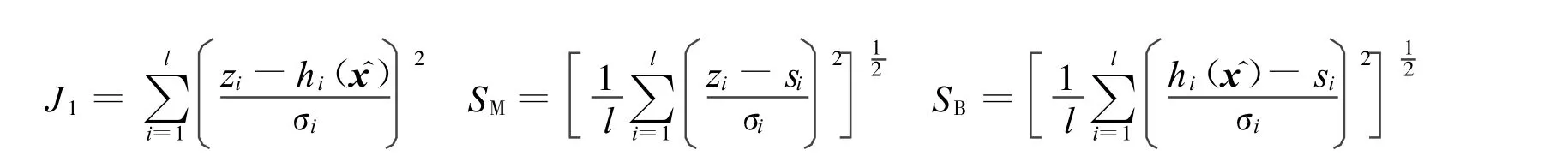
式中:l——量测量数;si——量测量 i的真值.

据此通过算例仿真对结合AD技术的多平衡机状态估计模型的性能进行验证，结果如表2所示.从表2结果可见:相对于传统的状态估计，基于AD技术的多平衡机状态估计的精度得到了提高，由此可见，在多平衡机下状态估计的结果更符合实际状态.同时，J1基本都接近量测冗余，SM接近 1，SB小于 1，滤波效果明显，进一步说明了本文算法是有效的.

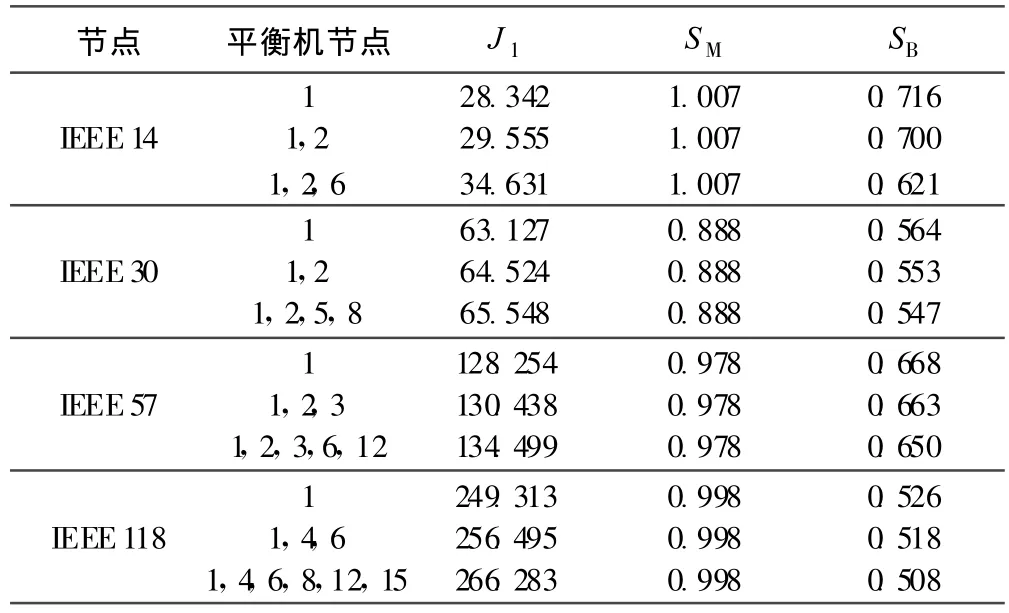
表2 结合AD技术的多平衡机状态估计的性能参数Table 2 Performance parameters in state estimation for multi-balancing machines with AD technology

4 结 语

本文引入多平衡机思想，在经典加权最小二乘法的基础上提出了计及多平衡机的状态估计算法，它能完整地计及多平衡机对电力系统的影响;提出运用ADOL-C工具获得量测函数的雅可比矩阵，减少了算法的计算量，提高了计算效率.通过对IEEE14节点等4个标准系统的仿真验证了算法的有效性.结果表明，基于AD技术的多平衡机状态估计算法在电力系统运行与控制中具有一定的应用价值.

[1]于尔铿.电力系统状态估计[M].北京:水利电力出版社，1985:61-104.

[2]贾嵘，蔡振华，刘晶，等.基于主成分分析和最小二乘支持向量机的电力系统状态估计[J].电网技术，2006，30(21):75-77，98.(JIA Rong，CAI Zhen-hua，LIU Jing，et al.Power system state estimation based on principle component analysis and least square support vector machines[J].Power System Technology，2006，30(21):75-77 ，98.(in Chinese)).

[3]李碧君，薛禹胜，顾景汶，等.电力系统状态估计问题的研究现状和展望[J].电力系统自动化，1998，22(11):53-60.(LI Bijun ，XUE Yu-sheng，GU Jing-wen ，et al.Status quo and prospect of power system state estimation[J].Automation of Electric Power System ，1998 ，22(11):53-60.(in Chinese))

[4]任江波，于尔铿，郭志忠，等.基于灵敏度分析的逐次追踪状态估计[J].电网技术，2007，31(7):64-68.(REN Jiang-bo，YU Erkeng，GUO Zhi-zhong，et al.Sequential tracking state estimation based on sensitivity analysis[J].Power System Technology，2007，31(7):64-68.(in Chinese))

[5]庞博，卫志农，孙国强.基于风力发电机简化RX模型的电力系统状态估计[J].电网技术，2009，33(19):159-163.(PANG Bo，WEI Zhi-nong，SUN Guo-qiang.Power system state estimation based on simplified RX model of wind power generator[J].Power System Technology，2009，33(19):159-163.(in Chinese))

[6]崔丽华，陈根军.多平衡机潮流计算在调度员潮流中的应用[J].广东电力，2006，19(9):13-17.(CUI Li-hua，CHEN Gen-jun.Application of multi-slack load flow calculation in dispatcher power flow[J].Guangdong Electric Power，2006，19(9):13-17.(in Chinese))

[7]杭乃善，姚元玺，窦婷婷，等.基于直角坐标注入电流形式的多平衡节点潮流算法研究[J].继电器，2005，33(4):9-16.(HANGNai-shan ，YAO Yuan-xi，DOU Ting-ting，et al.An algorithm of multi-balance bus based on rectangular coordinate current influx[J].Relay ，2005，33(4):9-16.(in Chinese))

[8]罗纯坚.多调频厂下的电力系统潮流计算[D].北京:华北电力大学，2007.

[9]许继红，陈亚宁，林莉，等.一种改进的配电网牛顿潮流算法[J].广东电力，2008，21(5):15-18.(XU Ji-hong，CHEN Ya-ning，LIN Li，et al.An improved Newton power flow algorithm for distribution network[J].Guangdong Electric Power，2008 ，21(5):15-18.(in Chinese))

[10]姚元玺，杭乃善.基于联络线功率等值约束条件的潮流算法研究[J].继电器，2006，34(1):31-33.(YAO Yuan-xi，HANG Naishan.Power flow studies of multi-swing bus based on tie-line power equivalence constraints[J].Relay，2006，34(1):31-33.(in Chinese))

[11]BARTHOLOMEW-BIGGSM C ，BROWNS ，CHRISTIANSON B，et al.Automatic differentiation of algorithms[J].Journal of Computational and Applied Mathematics，2000，124:171-190.

[12]张海斌，薛毅.自动微分的基本思想与实现[J].北京工业大学学报，2005，31(3):332-336.(ZHANG Hai-bin，XUE Yi.On automatic differentiation[J].Journal of Beijing Polytechnic University，2005，31(3):332-336.(in Chinese))

[13]李萍.自动微分工具实现技术研究[D].长沙:中国人民解放军国防科学技术大学，2002.

[14]ORFANOGIANNIT，BACHER R.Using automatic code differentiation in power flow algorithms[J].IEEETrans on Power System，1999，14(1):138-144.

[15]耿光超，江全元.基于自动微分技术的内点法最优潮流算法[J].电力系统自动化，2008，32(23):41-45.GENG Guang-chao，JIANGQuan-yuan.An automatic differentiation based interior-point method for optimal power flow[J].Automation of Electric Power System ，2008 ，32(23):41-45.(in Chinese))

[16]IBSAISA，AJJARAPUV.The role of automatic differentiation in power systems analysis[J].IEEETrans on Power Systems，1997 ，12(2):592-597.

[17]JEROSOLIMSKI M，LEVACHER L.A new method for fast calculation of Jacobian matrices:automatic differentiation for power system simulation[J].IEEETrans on Power Systems，1994，9(2):700-706.

[18]WALTHERA，GRIEWANK A.A package for the automatic differentiation of algorithmswritten in C/C++[CP/OL].(2010-11-18).http://www.coin-or.org/projects/ADOL-C.xml.