关于三点式振荡器关键问题的探讨
2012-10-12于红兵张金华
于红兵,张金华
(成都信息工程学院通信工程系,四川成都610225)
三点式振荡器作为常见的振荡电路获得了普遍的应用,但关于它的工作机制的描述,在现有“高频电子线路”课程教材的理论分析中,仍然有一些值得商榷之处[1-5]。
本文从振荡器的信号特点入手,结合反馈型振荡器的结构特点,引出复频域环路增益与相量形式的环路增益的概念,并对两者的不同取值特点加以分析,得到环路增益的一般计算原则。为了方便地求出某些较为复杂的振荡器的环路增益,本文提出了一种较为简便的算法,并应用到三点式振荡器的计算中,分析三点式振荡器起振条件关键问题的细节。笔者还讨论了这一计算过程及其计算结果与传统认识的不同之处,并且用相应的实验加以验证。
1 环路增益概念
文献[6,7] 提出了电路起振是零激励线性电路的本征问题,信号模式为est。文献指出有普适意义的电路起振条件判据是:存在复数s0,使复频域中的环路增益T(s0)=1,而且Re(s0)>0,Im(s0)≠0。s0正是微分方程通解所涉及的特征根,而T(s0)=1是特征方程,以上条件说明特征根在复平面的右半平面。所以,复频域形式的环路增益与通常的相量形式的环路增益相比较,前者是更基本的概念。然而复频域形式的环路增益到底从何而来呢?本文将阐释如下。
起振时信号模式为est,说明所有电路变量均以est的形式变化,因而任意两个电路变量之间将保持固定的比例系数(一般为复数)。
对于反馈型振荡器而言,如果能进一步找到电路变量y1,y2,…,yn之间一一对应且各不相同的约束关系并构成闭合的约束链:y2=K1y1,y3=K2y2,…,yn=Kn-1yn-1,y1=Knyn。则有:y1=KnKn-1…K1y1。由于y1≠0,因此KnKn-1…K1=1。又由于电路中存在电抗元件,因而K1,K2,…,Kn中至少有一个与s有关。所以KnKn-1…K1=1是s的函数,可称为复频域形式的环路增益,记为T(s)。KnKn-1…K1=1即为T(s)=1,可由此解出特征根s=s0,因而这一关于特征根的方程正是特征方程。另一方面,T(s0)=1等价于T(s0)y1=y1,其物理意义在于:无论电路处于何种状态(起振时或达到平衡后),反馈量与原值一定相等。
以上分析既给出了复频域形式环路增益的构造性定义,又阐述了它在实际电路中必然取值为1的理由,同时还引导出了它的一般计算方法。文献[7] 中,对如图1所示的共射变压器耦合振荡器环路增益的计算正是遵循了这种方法,从而得到了与仿真实验结果相吻合的起振条件。其约束关系为
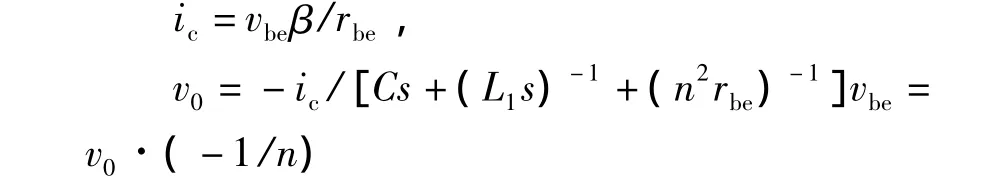
上式中,rbe是晶体管的共射交流输入电阻,β是晶体管的共射交流电流放大倍数,n是变压器的匝数比

图1 共射变压器耦合振荡器
因而复频域形式的环路增益为
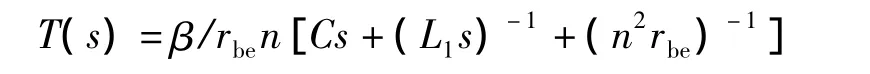
文献[6] 肯定了用相量法同样可以表达起振条件。通常,一个振荡器能够在某个ω1处满足T(jω1)>1,且T(ω)/ω|ω=ω1<0,该振荡器便可以起振。T(ω)是T(jω)的幅角。这里这一相量形式环路增益T(jω1)>1的要求与起振时复频域形式环路增益T(s0)=1的要求并不矛盾。其要点在于,jω1并不是起振时的特征根,分析相量形式的环路增益T(jω)即是讨论复频域形式的环路增益T(s)在虚轴上的取值特点,而这有助于判断特征根到底是在右半平面还是在左半平面。如此一来,就可以不用求解特征方程(它常常转化为难解的高次方程),从而可以简化计算。
2 常见振荡器的环路增益计算
常见振荡器的结构都可以用图2的形式表示。它由一个三端口网络和一条反馈线构成,其中三端口网络内部的反馈可忽略。以图1所示的共射变压器耦合振荡器为例,去掉反馈线后,A点、B点和地之间的电路构成三端口网络,这个三端口网内部的反馈可忽略。
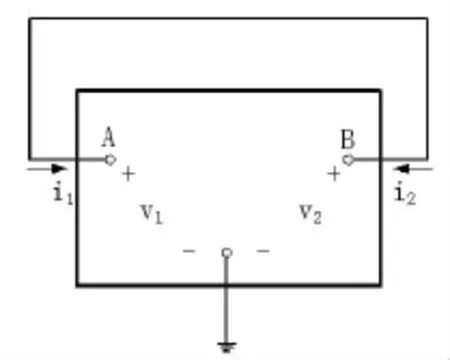
图2 振荡器结构图
首先,对三端口网络可应用双口网络的Z参数等效,其伏安关系为

由于三端口网络内部的反馈可忽略,故Z12=0。用Z参数等效电路取代三端口网络,得到图3所示的与原振荡器等价的电路。
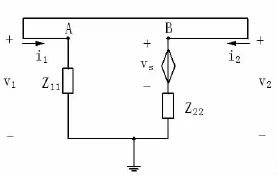
图3 图2所示振荡器的等效
此电路中,在电路变量i1与vs之间存在着由两个不同的约束关系构成的闭合约束链为?
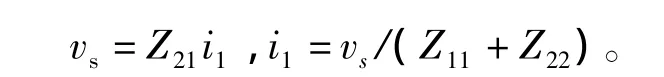
根据环路增益的构造性定义,有

以共射变压器耦合振荡器为例,有
Z11=rbe,Z22=1/[Cs+以及Z21=β/n[Cs+] ,由此得到的环路增益与前面直接在原振荡器中讨论的结果相同。
式(2)中需要计算的量都是三端口网络的Z参数,因此这种计算环路增益的方法可称为环路增益的Z参数算法。类似地也可以推导出环路增益的g参数算法和h参数算法等。这些算法在计算时考虑的对象已经不是含有反馈线的原振荡器,而是去掉了反馈线的三端口网络。这将切断原电路中的反馈联系,在不少情况下,电路对象的结构复杂性将大大降低,环路增益的计算也就成为可能。
3 三点式振荡器的完整分析
三点式振荡器其交流通路如图4所示。该电路所需元件不多,但其结构的复杂性并不低。对此,不少教材中认为三个电抗元件X1,X2和X3构成谐振回路[2-5],因此令X1+X2+X3=0作为谐振条件,以此为逻辑起点用于推导其他关系。笔者认为,这是值得商榷的。因为谐振这个概念在其一般意义上指的是在某个频率下端口特性为纯电阻(包括零和无穷大),不可能针对某个电路再给出一个不同的定义。对于三点式振荡器中的三个纯电抗元件,这是不会出现的现象(阻抗不可能成为实数或无穷大)。

图4 三点式振荡器的交流通路
如果采用环路增益的Z参数算法,X1+X2+X3=0将成为以下推导的一个成果,从而可以重新理出一条分析的线索。图4已经将三点式振荡器画为由一个三端口网络和一条反馈线构成。去掉反馈线,考虑剩下的三端口网络。当三极管内部的反馈可忽略时,有
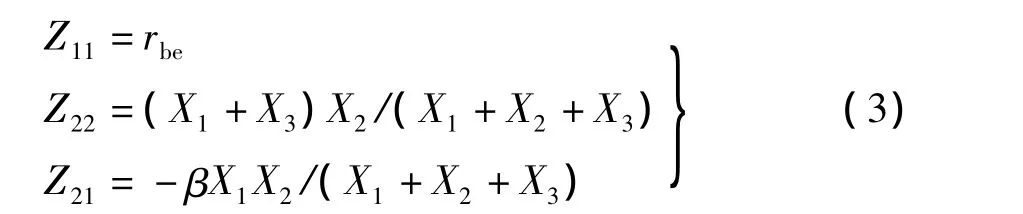
将上式代入式(2)中,得到
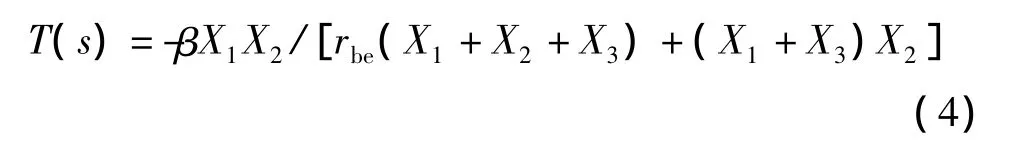
如果求特征根,则将面临求解至少三次方程的问题,所以需要转而以相量法进行分析。这时X1,X2和X3都是虚数,如果要求T(jω1)>1,为保证T(jω1)为实数,考虑到式(4)分子项和分母第二项都是实数,则必有

因此,X1+X2+X3=0并不是由于存在谐振而引出的结论。而T(jω1)=β·X1/X2>1,即

这就是三点式振荡器的定性要求(即:“X1,X2的电抗符号应相同,X3与X1,X2的电抗符号应相反”)的理论依据。根据文献[6] ,起振时还要求T(ω)/ω|ω=ω1<0。现证明如下。
所要解决的问题是:如果在ω1处使X1+X2+X3=0,要证明在β>X2/X1(即T(jω1)>1)的情况下r(ω)/ω|ω=ω1<0。为此在很接近于ω1的ω2=ω1+Δω(ω1>>Δω>0)处,考察T(jω1)的取值情况。根据式(4)有
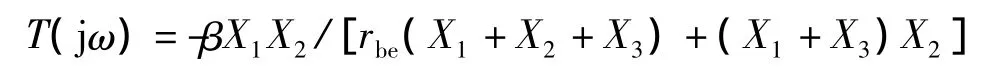
当ω=ω1时,分子和分母第二项为正实数,分母第一项为零,T(ω=ω1)=0;当ω=ω2=ω1+Δω时,由于Δω很小,分子和分母第二项仍将保持为正实数,记X1=jx1,X2=jx2,X3=jx3。若有x1+x2+x3>0,则T(ω=ω2)<0,使T(ω)/ω|ω=ω1<0。于是问题转化为求证(x1+x2+x3)/ω>0。考虑到X1,X2和X3原则上分别都是电抗元件的混联。如果将这种混联后的电抗值统一地记为x,则需一般性地证明x/ω>0。
我们采用数学归纳法:首先,对于单电感或单电容,其电抗值分别为ωL和-1/ωC,得到(ωL)/ω和(-1/ωC)/ω都是大于零的;其次,设XA和XB分别是两个由电抗元件混联而得的单口网络的电抗值,若xA/ω>0,xB/ω>0,则串联后的电抗值(xA+xB),及并联后的电抗值,可统一地记为x,都满足x/ω>0。根据以上两点可以推论,任意电抗元件混联后的电抗值都满足x/ω>0。因而T(ω)/ω|ω=ω1<0得证。
对于本文分析与传统分析的不同之处,还可以设计以下两方面的仿真实验加以验证:
(1)可以验证β大于X2/X1即可起振,β小于X2/X1时不能起振;
(2)电路中电路变量存在以下关联关系为

前一个式子代入后一个式子,就可以得到i2与i1之间的关系式为
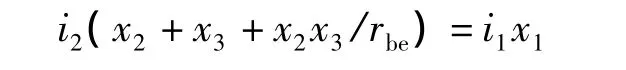
进而得到vx2与vx1的比(即所谓反馈系数为
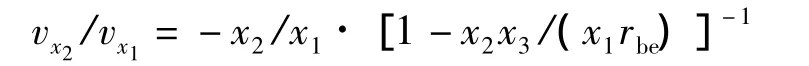
对于电容三点式振荡器,有

这说明反馈系数一般为复数,而不是如文献[2,3,5] 所述的实数。这一点很容易用仿真实验来验证(电感三点式振荡器也可进行类似验证)。
4 结语
本文推进了笔者关于复频域环路增益的认识[6,7],引入了复频域形式环路增益的构造性定义,得到环路增益的一般计算原则。针对相量形式环路增益,强调了T(jω1)>1的要求与起振时复频域形式环路增益T(s0)=1的要求并不矛盾。
为了能够比较方便地求出某些较为复杂的振荡器的环路增益,本文提出了环路增益的Z参数算法。进一步将此算法应用到三点式振荡器的计算中,用相量形式讨论了此电路的起振条件以及电压分配方式等相关问题,对于此电路的若干关键问题提出了本文的观点。
最后,这些分析的定量结论经过了实验检验,这两种实验的结果都很好地证实了本文的相关分析结论,说明这一分析过程确实反映了三点式振荡器的工作机制。
[1] 谢嘉奎,宣月清,冯军.《电子线路(非线性部分)》[M] .北京:高等教育出版社,2000
[2] 阳昌汉.《高频电子线路》[M] .哈尔滨:哈尔滨工程大学出版社,2000
[3] 于洪珍.《通信电子电路》[M] .北京:电子工业出版社,2002
[4] Muhammad H.Rashid.《Microelectronic Circuits:Analysis and Design》[M] .United States of American:PWS,a division of Thomson Learning,1999
[5] 曾兴雯,刘乃安,陈健.《通信电子线路》[M] .北京:科学出版社,2006
[6] 于红兵.反馈型振荡器起振条件的新研究[J] .成都:电子科技大学学报,2005,34(4):573~576
[7] 于红兵,王天宝.反馈型正弦波振荡器起振的元件参数分析[J] .成都:四川师范大学学报,2005,28(6):744~746
