基于最小二乘原理的炼焦配煤控制方案

刘春梅

LIU Chun-mei

（柳州职业技术学院，柳州 545006）

0 引言

目前冶金行业对焦炭的质量要求越来越高，而焦炭的来源主要是通过各种原煤按一定配比形成配煤通过炼焦过程所得到，由于在这一过程当中每个环节都有可能对最终生成的炼焦焦炭质量产生影响[1]，因此目前在炼焦厂生产过程当中如何控制焦炭质量成为一个首要的难点问题[2]。传统的炼焦生产过程中往往是根据原煤的情况按照一定的经验配比，得到配煤再进行炼焦试样，通过试样来分析和检测所得到的焦炭是否满足冶金企业的需求[3]。在这一过程当中对配煤的质量控制工作量非常大，也非常耗时，并且一旦发现所生产出来的焦炭不符合预期的要求则需要重新进行配煤，如此反复的过程会消耗炼焦企业大量的人力和物力，并且也会导致炼焦生产的效率非常低下。为了解决炼焦企业当前所面临的这种困境，因此非常有必要研究对焦炭质量预测和生产控制的方法。目前，传统的焦炭预测方法采用的基本上都是基于数据挖掘和人工智能的方式进行处理[4]，这种处理过程相对来讲比较复杂，而且也对模型建立的能力和模型的分析能力都提出比较高的要求，数据分析过程也非常长，而对于现代工业生产而言，由于焦炭的质量只需要满足一定的数值范围即可达到需求，而不是必须满足一个特别精确的数值[5]，因此在实际生产中如何设计和实现一种快速的焦炭质量预测模型既能够满足炼焦企业对质量控制的需要，又能够降低企业的分析和控制成本[6]，为此本文提出了一种基于最小二乘原理的炼焦配煤方案。

该方案的设计思想是通过炼焦所使用的各单种原煤的质量因子和各种配煤之间的质量因子之间建立数学模型[7,8]，分析单种煤和配煤之间的质量影响关系，通过该模型的研究和应用建立起一套借助单种煤精确预测配煤质量因子的方法和过程，再由配煤的质量因子去预测和控制焦炭的质量[9,10]。因此这种设计方法具有实现速度快，控制精度基本能满足炼焦企业现实需求的特点。

1 炼焦配煤的质量参数因子

炼焦配煤的来源是按照一定比例对各种单种煤进行配比及混合研磨之后形成的。由于配煤是由各种单种煤所组成的，因此配煤的各种质量参数直接由每一种配合的单种煤质量来决定，而配煤的质量又最终影响着焦炭的质量[11]。在炼焦质量预测与控制问题当中，一般主要是研究从配煤的各种指标参数到炼焦质量的各种指标参数之间的关系，但是配煤的质量又取决于各单种煤的质量，因此各个单种煤和配煤之间的参数关系同样需要进行深入的研究[12]。目前针对炼焦用煤的这一问题，对单种煤的质量研究主要关注的质量参数有：煤的灰分、硫分、水分、挥发分以及粘结系数[12]。

这些参数对最终炼焦生成的焦炭质量都有着非常直接的影响，比如煤炭中的水分所表明的是这一单种煤当中所含有水分的比率，在炼焦过程当中煤炭会被隔绝空气而加热，在加热过程中水分会变成水蒸气而蒸发掉。如果炼焦配煤中水分含量过高会导致炼焦过程中对热量消耗过大，并且生成出来的焦炭时间会更长，生产效率更低，甚至水分过高会降低焦炭的强度。配煤中的灰分反应的是原煤中所含有的各种不可燃也不参与化学反应物质的比率，一般是由杂质、灰尘、泥沙等组成。从炼焦生产过程来分析，灰分的含量对炼焦生产是没有任何帮助，并且在原煤当中如果灰分含量过高，会导致炼焦生成的焦炭杂质含量较高，从而降低焦炭的透气性和物理强度。硫分是指原煤当中含硫的百分比。由于炼焦生成的焦炭一般是用于冶金领域，而在金属冶炼过程当中硫是属于有害物质，而且金属冶炼过程中掺杂到金属中的硫主要是来自焦炭，为了提高金属的冶炼纯度，需要严格的控制硫的百分比，这也就是说需要严格的控制炼焦生产的焦炭中硫的含量，因此对原煤当中硫分的含量也就有着严格的要求。挥发分指的是单种煤在炼焦过程中质量损失的数量，即质量挥发的部分，原煤的挥发程度对炼焦过程中生成的焦炭质量有着直接的影响，主要表现在影响焦炭的粘结性和焦炭的强度。粘结系数指的是原煤在炼焦过程当中生成焦炭之后使焦炭具有的耐磨特性和粘结特性，这个参数也是直接影响着炼焦生产的焦炭质量的重要指标，因此在对配煤成分分析的时候也需要纳入这一质量因子进行统一分析。

目前用于炼焦厂炼焦使用的配煤来源渠道各不相同，有的原煤质量比较高，属于低水分，低硫分，低灰分，高热量煤；而有些煤炭则含有各种杂质，且比例比较高，如果把这些原煤直接用于炼焦，生成的焦炭质量将不能达到焦炭的质量要求，因此需要对各种原煤按照一定的比例进行调配，使得不同质量条件的原煤都能够最终送入到炼焦厂进行炼焦生产，最终生产出符合质量要求的焦炭。

2 炼焦配煤控制模型

炼焦配煤是通过各种原煤按一定比例配比之后所得到的。由于在配比过程当中只有物理上的研磨和煤炭的混合，不存在任何的化学反应，因此从各种原煤的质量参数到配煤的质量表述形式之间，可以采用线性关系的控制模型来建立其相互之间的关系。根据本文所研究的炼焦配煤的质量参数因子，对每个单种煤分别选取五个参数作为评价单种煤质量的参数因子。假设用变量分别来表示配煤中的五个质量因子，与之相对应的每一种煤，也都将有这五个参数所描述的质量向量。因此建立的配煤各质量参数和单种煤质量参数之间的数学关系如式(1)所示。

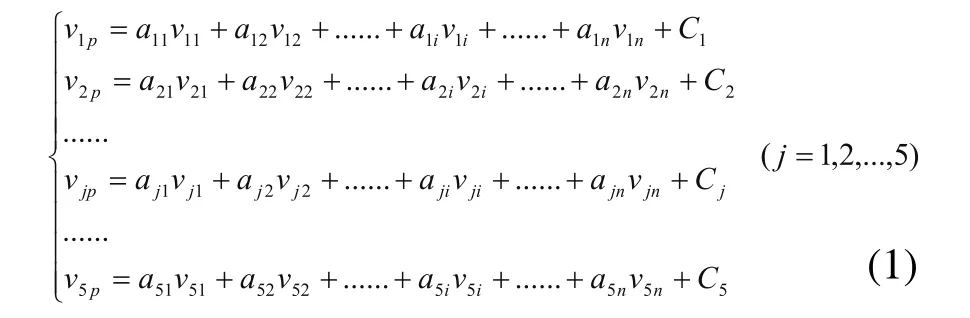
该公式总共假定进行配煤的原煤种类共有n 种，即有n个备煤选项，每一种备煤都选取了v1到v5五个质量因子，分别用v1i～v5i表示，其中i=1,2,3...,n,该公式中vji表示第j个质量因子在有n个备煤的第i种煤的影响系数。在式中，v1p～v5p分别表示通过这n个备煤所混合形成的配煤当中，质量因子v1～v5的数值。式中C1～C5所表示的含义是在建立每一个单种煤的质量因子与配煤的质量因子之间的线性关系时所附加的常量，该常量反应的也是单种煤与配煤之间的质量因子之间的估计误差，如果配煤和单种煤之间的质量关系满足完全的线性关系，那么C1～C5应该都等于0，如果配煤和单种煤之间的线性关系不满足完全的线性关系，那么用该线性模型分析单种煤与配煤之间的质量关系时，需要尽可能的使得C1～C5的质量关系均趋近于0，因此，在C1～C5的实际所选数值中，每个Cj的值应该是满足式(2)所述的关系式：

即Cj应该是一个中心值为0的正态分布变量。对式(1)采用下列公式来表示可以得到的简化的公式如式(3)所示。

在公式3中，v1p～v1p是需要进行计算的结果值，矩阵n和向量c都是该模型的系数，需要通过大量的样本数据对模型进行大量的反复训练和不断的修正误差最终得到的系数值。矩阵v'表示的是n个备煤当中，每一个质量因子的测量值，在确定的n个备煤之后，可以通过专用的仪器对备煤进行测量获取每一个参数因子的准确数值，因此该模型已经建立起了各种单种煤和备煤的质量因子之间的模型关系，那么下一步将要解决的问题是对该模型中的参数系数A、C进行求解。

3 基于最小二乘原理的模型参数求解

根据本文所建立的炼焦配煤控制模型，需要对模型进行求解的是两个系数矩阵，而对这两个系数矩阵的计算是需要通过大量已知样本集的分析和模拟，通过样本集中给定的输入和输出关系，利用本文所建立的控制模型计算出与样本集最为接近的系数矩阵。本文在选取样本集进行模型参数求解的时候所用的样本数据共有500条。

通过样本数据去寻找所有解空间当中能够使得Cj取最小值的系数矩阵系数A，为了能够在所有的解空间当中搜索得到满足条件的最优解，本文采用了基于最小二乘原理的解空间搜索方法，该方法的核心思想是对所有的解空间进行搜索，在选定一个解空间A'之后计算当期的Cj数值，如果当前得Cj数值比前一次计算的结果更小，则以当前的解空间A'作为更优的解。然后再选取其他的满足条件的解空间的数值A''，如果A''计算得到的Cj值更小，那么A''又将作为更优的解空间；如果A''得到的Cj值更大，则A''的结果直接丢弃，仍然保留之前的A'作为最优解，如此类推一直循环下去直到寻找到Cj在所有搜寻的解空间当中取得最小值的解为止。此时所得到的解即为满足条件的最优解，作为该模型的系数A。本文在计算过程中借助于MatLab工具实现了基于最小二乘原理的模型参数的求解，通过该工具最终计算得到的最优解结果如式(4)所示：

至此得到了炼焦配煤中单种煤和配煤之间的控制模型，利用该控制模型可以再选取一批的数据进行误差的修正，本文在计算该控制模型的时候所选取的样本参数事实上已经是多次的误差修正之后最终形成的最优的样本集合。因此在论文分析过程当中不再阐述误差修正的过程。当模型建立起来之后，本文对所建立的模型又选取一定的数据进行测试验证，结果如图1所示。图中所选取的测试参数时配煤的硫分，从图中所反映的结果可以看出本文所建立的配煤质量预测的结果和实际的利用本文所进行的模型而预测出来的质量因子与实际测量的配煤的质量因子误差非常小，绝对误差小于0.5%，基本上可以达到炼焦配煤各种质量指标的需求。

图1 基于最小二乘原理的配煤质量预测测试结果

4 炼焦配煤实现方案

根据本文所建立的炼焦配煤控制模型，可以对炼焦配煤中个单种煤的选取配比是否合理进行判断，并实现炼焦配煤的自动检测和控制。利用该模型所设计的炼焦配煤检测控制方案如图2所示。

图2 炼焦配煤检测控制方案

图2中，首先根据炼焦厂能够得到的原煤情况进行原煤的选取，在原煤选取的时候主要根据原煤的进货渠道和原煤性价比来决定；选取了一定的原煤之后，按照原煤配比的经验规律制定出每一种原煤的配比值。然后再对原煤的质量因子进行测量，获取每一种原煤的主要的质量因子参数，之后利用本文所设计的配煤质量控制模型对配煤的各质量因子进行预测，得到预测之后的配煤的各质量因子，接下来对所得到的配煤的各质量因子进行判断，断定其是否能够满足炼焦的需求。目前对配煤质量因子的判断条件有一些成熟的研究理论和经验值，都给出了配煤所应该满足参数条件，本文在构造配煤选煤方案的时候所选取的配煤各质量因子的标准如表1所示。

表1 配煤各质量因子的标准

按照表1所设定的配煤应该满足的质量要求，如果当前所得到的配煤质量指标不符合该要求的时候，则人工对原煤的选取配比进行调整，主要调整的依据是根据当前质量因子中不满足的因子项数选取加大满足该因子配比的原煤比例，而降低不符合该因子的原煤配比，通过这种不断的循环调整原煤的配比情况，最终使得到的原煤配比数值所生成的配煤质量能够满足表1所示的焦炭需求，即表明完成当前对炼焦的配煤方案。目前利用这一方案所构造的炼焦配煤的实现方案，经过实践检验，得到的配煤配比情况能够满足炼焦厂的炼焦需求，利用该方案所生产的配煤也能够生产出符合质量要求的焦炭，提高了炼焦厂配煤生产的指导性和科学性。

5 结束语

由于目前对炼焦配煤有一些经验性的质量控制指标，因此研究各单种煤与配煤之间的质量影响关系可以比较快速的实现炼焦配煤的控制过程，并且所得到的配煤基本上都能够满足炼焦配煤的需求。本文所设计的基于最小二乘原理的炼焦配煤控制方案具有实现速度快，配煤质量控制精度比较高的优势，因此利用本文所设计的配煤方案基本上能够满足现有炼焦厂的配煤需求，但是需要说明的是本文所设计的配煤方案是以满足目前经典的配煤质量指标而设计的，在实现过程当中，满足这一炼焦需求的配比情况可能会有多种，而本文并没有对多种可能的配煤方案进行最终化的分析或者选取，如果要考虑炼焦厂的配煤整体经济效益或者其他的一些约束条件，则还需要对配煤的最优化问题进行深入的分析。

[1]程官江,刘阳,吴红桃.焦炭全自动质检系统的开发与应用[J].河南冶金.2010,18(03):29-31.

[2]郑文华,张晓光.提高焦炭质量的技术措施[J].河南冶金.2004,12 (05):5-7.

[3]王洪兴.7.63m焦炉焦炭质量在生产中的控制[J].燃料与化工.2010,41(04):36-36.

[4]单晓云,高志芳,赵树果,牛国强.模糊聚类分析优化炼焦配煤的研究[J].煤炭科学技术.2005,33(06):68-71.

[5]谢海深,刘永新,孟军波,吕庆.焦炭质量预测模型的研究[J].煤炭转化.2006,29(03):54-57.

[6]李维忠,李训智,玄冠红,常宇.焦炭质量全方位预警预控管理机制的建立与实施[J].山东冶金.2010,32(01):67-69.

[7]常爱英,吴铁军,包鑫,江爱朋.基于最小二乘支持向量机的动力配煤着火特性预测模型[J].煤炭学报.2010,35(08):1380-1383.

[8]王惠文,孟洁.多元线性回归的预测建模方法[J].北京航空航天大学学报.2007,33(04):500-504.

[9]郝洪洲. 配煤参数与焦炭质量[J].煤化工.2001,(04):20-22.

[10]任学延,张代林,张文成,许立信,王春花,郑明东.梅山焦炭质量预测模型的研究[J].煤化工.2010,38(01):31-33.

[11]郝晓静,杜钢,谢植,沈峰满. 模糊因果聚类模型在高炉焦比预测中的应用[J].东北大学学报.2005,26(04):363-366.

[12]王光辉,范程,田文中,余明程,刘智平,潘立慧,靳美程.焦炭质量预测方法的研究[J].武汉科技大学学报(自然科学版).2007,30(01):37-40.

[13]张群,吴信慈,冯安祖,史美仁.宝钢焦炭质量预测模型Ⅱ.焦炭质量预测模型的建立和应用[J].燃料化学学报.2002,30(04):300-305.