二维单裂隙-孔隙双重介质的核素迁移数学模型及参数反演

张 文， 阮周生， 邱淑芳， 何 杰

(1.东华理工大学放射性地质与勘探技术国防重点学科实验室，江西 抚州 344000;2.东华理工大学理学院 江西 抚州 344000)

90Sr是一种高毒性人工放射性核素，物理与生物半衰期均较长，资料显示核素90Sr在地下水中平均迁移1 km所需时间为104 a。在过去全球性核试验中，90Sr作为主要核污染物，各国对它在环境中的污染水平及动向进行了观测与研究(仵彦卿，2007;马应明等，2007;温瑞媛等，2000)。近年来，随着核能的广泛应用，各种核设施排放的废水中，90Sr仍是一个重要核素。在长期科研生产中积累了大量的含锶核废物，特别是在核设施退役过程中，产生了大量含锶极低放废物(VLLW)。核素在孔隙-裂隙中随地下水迁移问题从模型角度可分为单一介质迁移模型与双重介质迁移模型;从计算顺序角度又可分为两类，一类是正问题的研究，即采用何种方法解出满足模型要求的解。另一类则是反问题的研究，简单地认为是“由果溯因”思想，即根据测量数据来反推模型的特征(如水文地质参数、应力场等)。

关于正问题的研究，国内外的许多学者都取得了有意义的结论和在一定条件下的解析解(王榕树等，1994;刘金英等，1996;Ahsanuzzaman et al.，2003;Burnett，2001;Hatano et al.，1998;Gastberger et al.，2000;Borje，1986;Zhang et al.，1995;Pollner et al.，1999)。有学者较早地对核素在裂隙介质中迁移模型进行了研究，提出了用有限元与算子分裂迎风均衡格式相结合的方法求解放射性核素迁移方程(谢运棉等，1992)。近年来，杨勇等(2004)、郭敏丽等(2004)、王青海等(2004)先后进行了针对90Sr，137Cs，3H和Br－在不同条件下的迁移数值模拟研究;李寻等(2010)考虑了指数衰变注入源的基质域-裂隙域中溶质运移随地下水迁移的数学模型解析解。

由于反问题所求解的渗透系数、给水度、弹性释水系数、扩散系数等工程水文地质参数是工程设计的基本参数，一般通过工程地质钻探和抽水试验等勘探手段或通过经验公式获得，由于勘探手段代价高且受地域影响大，而经验公式回避了土壤结构的复杂性，缺乏坚实的物理基础，因而参数反演问题备受专家学者的关注，张东辉等(2003)、郁伯铭(2003)、刘建国(2001)、刘晓丽等(2004)将分形理论运用于多孔介质中，讨论多孔介质的渗透率、热导率、热弥散系数、水力参数等输运性质参数;张文等(2010)探讨了核素在单裂隙孔隙-裂隙双重介质中的一维迁移模型的解析解以及反演排污点源的反问题。

本文探讨了核素90Sr在孔隙-裂隙双重介质中的二维平面迁移模型正、反问题。利用Fourier变换和Saul’yev不对称差分格式相结合求得耦合模型的数值解。基于正问题的计算结果，采用遗传算法研究了迁移模型的参数反演问题，即根据裂隙中某测量位置的核素浓度反求裂隙迁移模型的裂隙介质水动力弥散系数D1和裂隙平均渗流速度u。数值结果表明，参数反演效果较好。

1 核素迁移的耦合模型

在张文等(2010)基础上，将迁移模型进行推广，由一维推广至二维平面迁移模型，同时探讨迁移模型的参数反演问题。考虑核素在一个二维平面饱和孔隙域中含有一条狭长裂隙的孔隙-裂隙双重介质中的迁移耦合模型，如图1所示，假定核素在裂隙域中有对流、弥散、衰减和吸附作用;裂隙宽度远小于岩块孔隙厚度，裂隙域为稳态的均匀一维渗流，孔隙域中的水流静止;含水层的吸附为物理吸附作用，符合等温线性吸附;核素衰减符合一阶衰减动力学方程;裂隙源头排污点源以指数递减形式注入核素。那么，核素在平面单裂隙多孔介质核素迁移过程耦合模型的基本微分方程(仵彦卿，2007;罗嗣海等，2005;李金轩等，2001;中国人民解放军总装备部军事训练教材编辑工作委员会，2002)为裂隙域迁移平衡方程:

为确保结果准确性，对模型进行帕克检验确定其是否具有异方差性。验证结果显示，F统计量的值为1.988844，Prob（F-statistic）=0.108443大于显著性水平α=0.05，说明模型不存在异方差性，证明模型不存在异方差性，模型设定完全可靠，回归分析结果可以作为分析结论以及政策建议的依据。

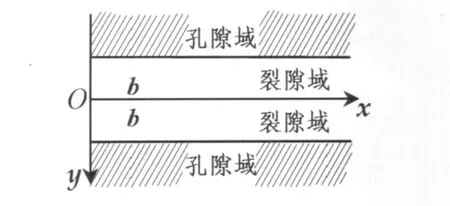
图1 单裂隙核素迁移示意图Fig.1 The schematic diagram of radionuclide migration in a single fracture

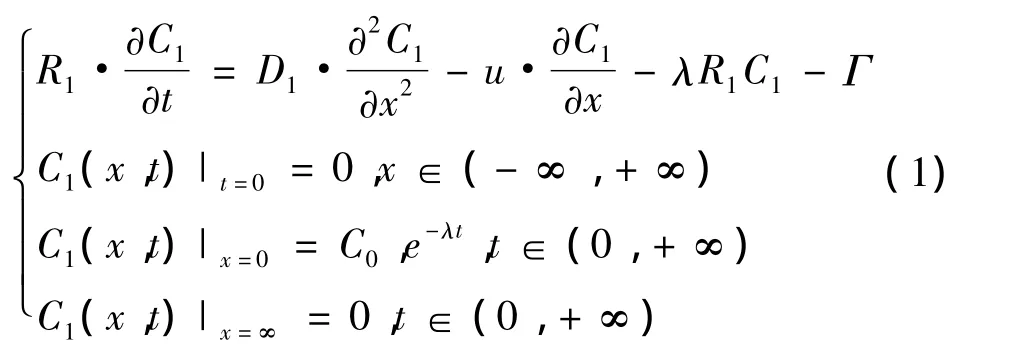
孔隙域迁移平衡方程:

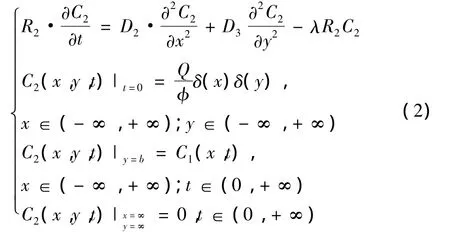
其中C1，C2分别表示裂隙域中核素的浓度和孔隙域中核素的浓度;D1表示裂隙介质水动力弥散系数;D2，D3分别为孔隙介质沿x方向和y方向的水动力弥散系数(x，y方向如图1所示);u为平均裂隙的渗流速度;λ为核素衰变常数;b为裂隙半宽;Γ为孔隙介质与裂隙域的溶质交换量。根据费克定律知，R1，R2分别为裂隙域的阻滞因子和孔隙域的容量因子，满足关系式，Q为污染物总质量，φ为岩石的有效孔隙度，ρb为岩石密度，Kf为吸附分布系数，Km为孔隙域中溶质平均分配系数，δ(x)为狄拉克函数。该模型对均质各向同性介质适用。

2 正问题的求解

本文所考虑的正问题是，已知裂隙源头排污点的核素浓度变化状态，求出核素浓度在裂隙和孔隙中的变化规律。为了能够求解耦合方程组，对孔隙域迁移平衡方程两边关于x和y进行二维Fourier变换，求出耦合项，再对裂隙域迁移平衡方程使用Saul’yev不对称差分格式的有限差分法求解得出数值解。

引进Fourier变换的相关符号，记

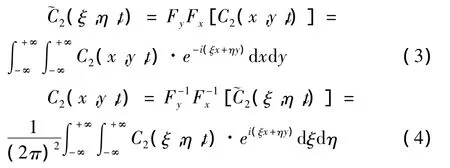
根据Fourier变换的性质容易得到

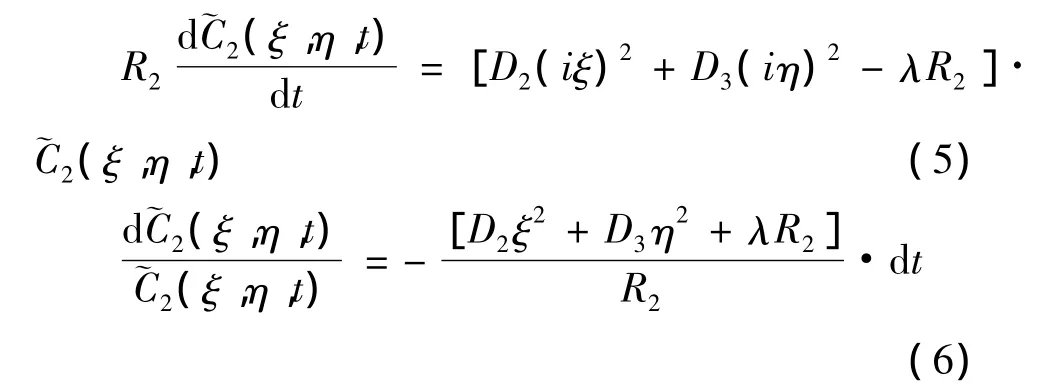
由已知条件

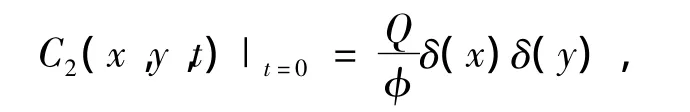
得到

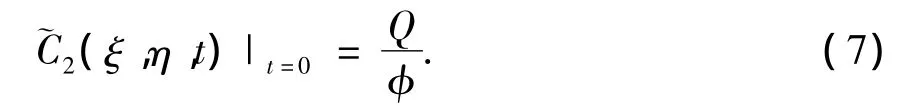
联立式(6)和式(7)，得出

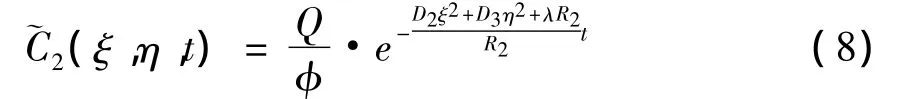
进一步使用Fourier逆变换式(4)以及位移性质，便得到核素在孔隙域中变化规律的解析解为

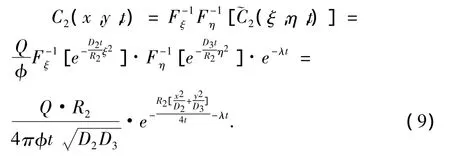
下面求解核素在裂隙域中变化规律的数值解。由式(9)易知

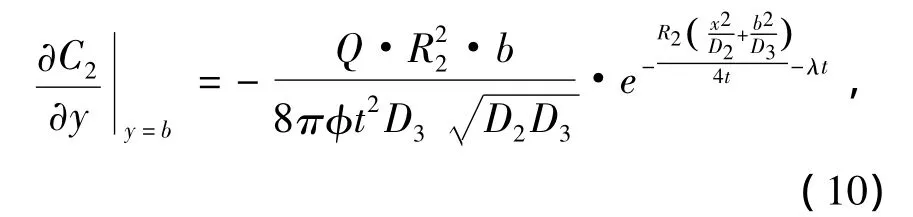
则耦合项为

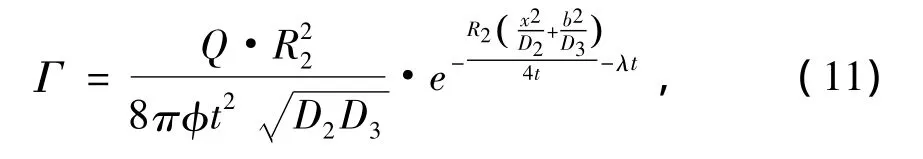
将耦合项代入裂隙域迁移平衡方程中得到定解方程

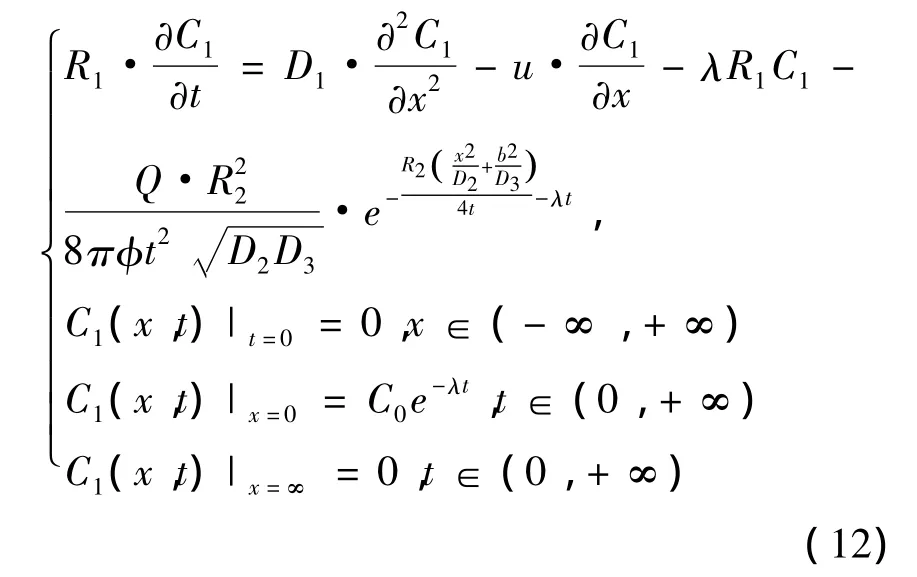
引进Saul’yev不对称差分格式，该差分格式是无条件稳定的(张文生，2006)，对于函数u(x，t)来说，其差分格式为

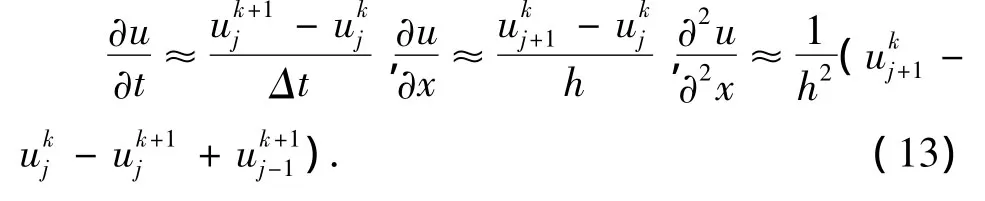
将式(11)离散后便容易得出核素在裂隙域中的数值解。

3 反问题的求解

考虑耦合模型中2个系数的反演问题，即在裂隙介质水动力弥散系数D1和裂隙平均渗流速度u未知情况下，通过附加某测量位置x0、不同时刻测得裂隙域中的核素浓度C1(x0，t)，T1≤t≤T2，来反求裂隙介质水动力弥散系数D1和裂隙平均渗流速度u。

记 f(t;D1，u)=C1(x0，t;D1，u)为已知 D1和 u经正问题求解出的浓度，设测量位置x0、不同时刻测得裂隙域中的核素浓度为h(t)，引进泛函

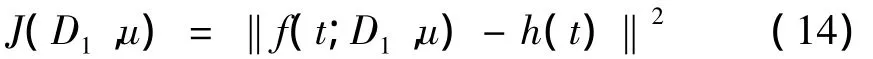
则反问题可归结为求参数D1和 u，使得泛函J(f)达到极小，即使得

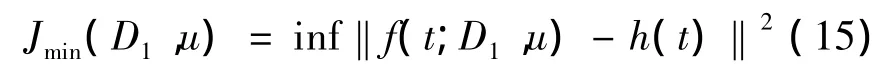
成立的D1和u就是系数反演反问题的最优解。

为探讨解决此类问题的有效方法，引进遗传算法。众所周知，遗传算法根据达尔文进化论中的“生存竞争”和“优胜劣汰”原则，不受求导和函数连续性的限定，从某一初始群体出发，借助复制、交叉、变异等操作，不断迭代计算，经过若干代的演化后，群体中的最优值逐步逼近最优解，直至最后达到全局最优(王彦飞，2007;王泽文等，2008;顾正华，2006;闵涛等，2004)。

遗传算法描述如下:

STEP 1 产生初始群体。在给定的参数范围内均匀随机生成实数编码建立初始群体，种群数量为N.个体中每个十进制数计算公式为

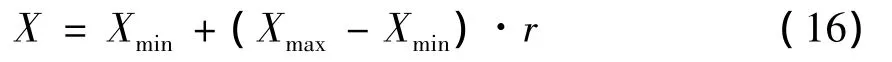
其中r为[0，1]服从均匀分布的随机数，X为个体目标变量，Xmin，Xmax分别为个体目标变量可取的最小、最大值。

STEP 2 交叉。将选出的采用综合交叉法将N个个体两两杂交，生成N个新的个体，交叉算法如下:

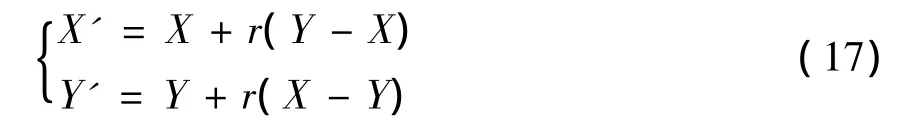
其中，X和Y为父代个体，X′和Y′为子代个体，r为[0，1]服从均匀分布的随机数。

STEP 3 计算适应值。取式(14)作为遗传算法的适应函数。

STEP 4 选择。对STEP 3中得到的由父代和子代共2N个个体的适应值进行比较，从中挑选N个更小的个体作为新一代个体。

STEP 5 变异。对STEP 4中选出的N个个体按照式(16)进行变异。

STEP 6、判断新一代群体是否满足结束条件，若满足则停机，否则转至STEP 2继续计算。

4 数值算例

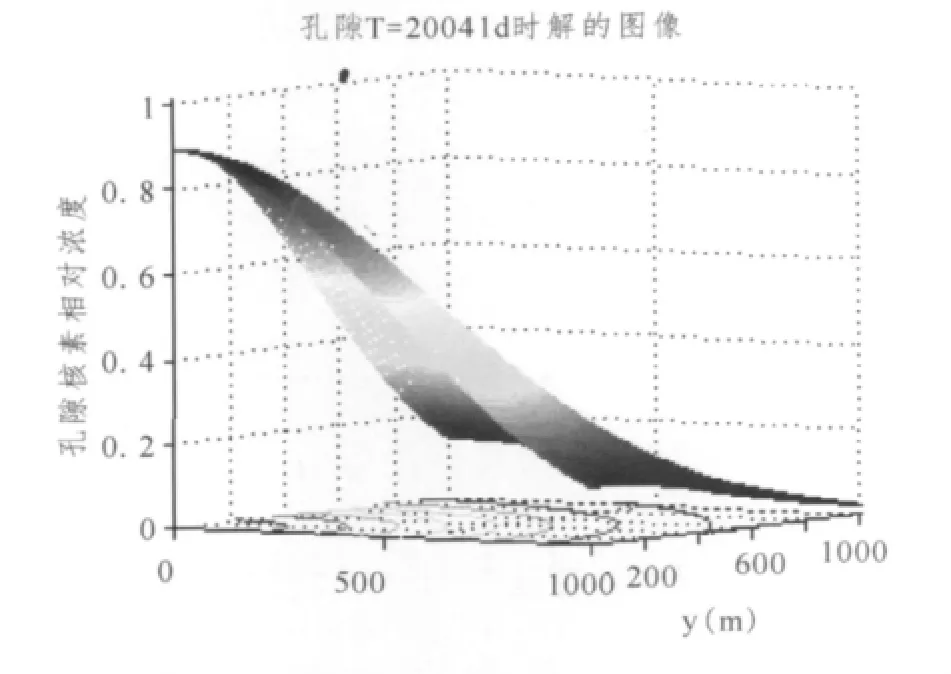
图2 平面孔隙中所含核素迁移规律Fig.2 Migration of radionuclides contained in the plane pore

给定计算参数(李录等，1998)。核素90Sr衰变系数 λ =1.54 × 10－4d－1，裂隙平均渗流速度 u=0.1 m/d，裂隙域的阻滞因子和孔隙域的容量因子分别为R1=1.0，R2=0.15，裂隙介质水动力弥散系数D1=0.351 m2/d，孔隙介质水动力弥散系数D2=1.38 × 10－5m2/d，D3=6.9 × 10－5m2/d，裂隙半宽b=2.5 × 10－5m.

实际问题中，测量数据往往带有测量随机误差。因此，通过 h(x)=C1(x，T)+ ε·C1(x，T)·R获得测量数据，其中C1(x，T)为正问题的解，ε为噪声水平，R为介于区间[－1，1]且服从均匀分布的随机数。遗传算法的参数设置如下:群体大小(30)，交叉概率(0.8)，变异概率(0.2)，参数范围(0.01，0.8)，终止代数(500)。

正问题的计算结果见图2～5，图2表示平面孔隙中所含核素当时刻T=20041 d时在平面上的分布图，图3表示平面孔隙中所含核素时刻T=20041 d，x=100 m时的变化规律，图4表示单裂隙中所含核素各个位置随时间变化的迁移规律，图5表示单裂隙中所含核素在测量位置x=506 m时随时间变化的迁移规律。

表1为在不同测量误差下的参数反演结果。图6为模拟裂隙x0=60 m，t∈[1 000，10 000]不同噪音水平ε时的测量数据。从表1可以看出，本文算法对于单裂隙核素迁移的耦合模型参数反演是有效的。

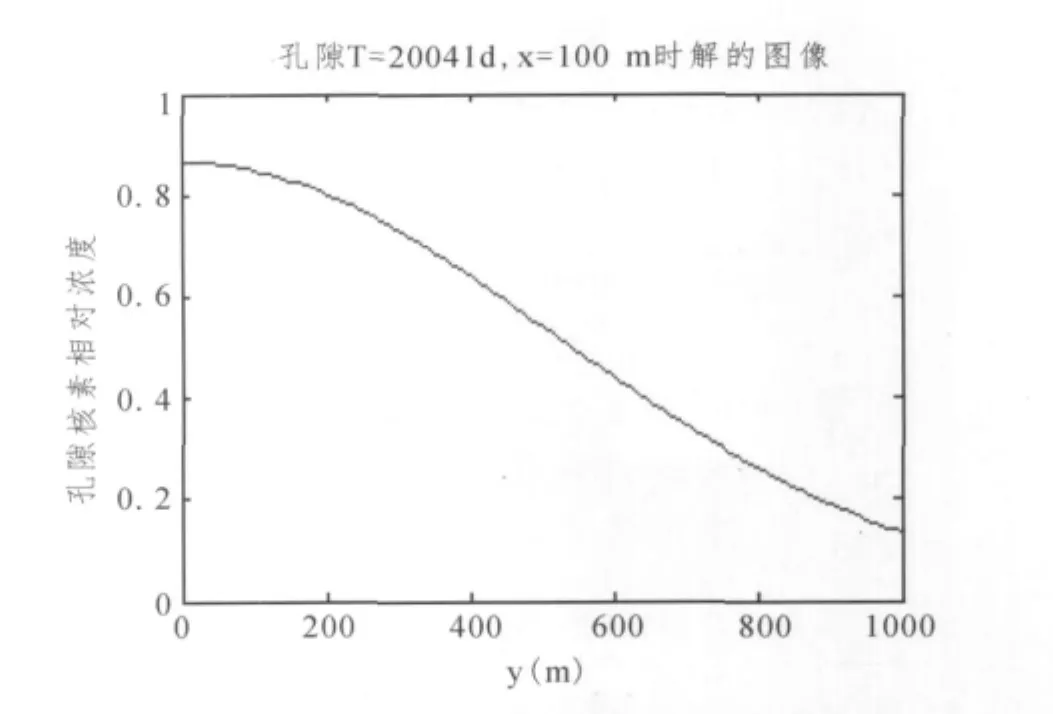
图3 平面孔隙中所含核素迁移规律(x=100)Fig.3 Migration of radionuclides contained in the plane pore(x=100)

5 结语

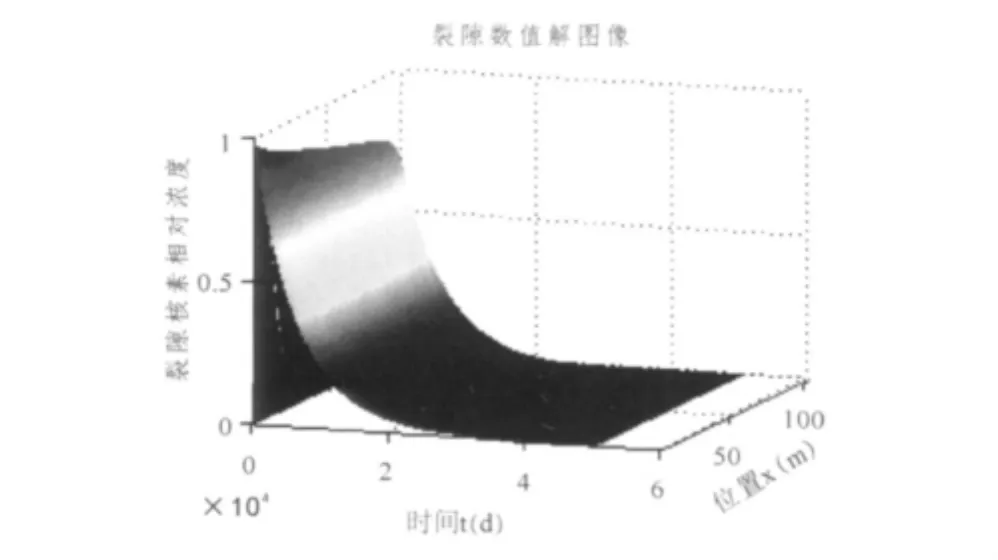
图4 单裂隙中所含核素迁移规律Fig.4 Migration of nuclides contained in a single fracture

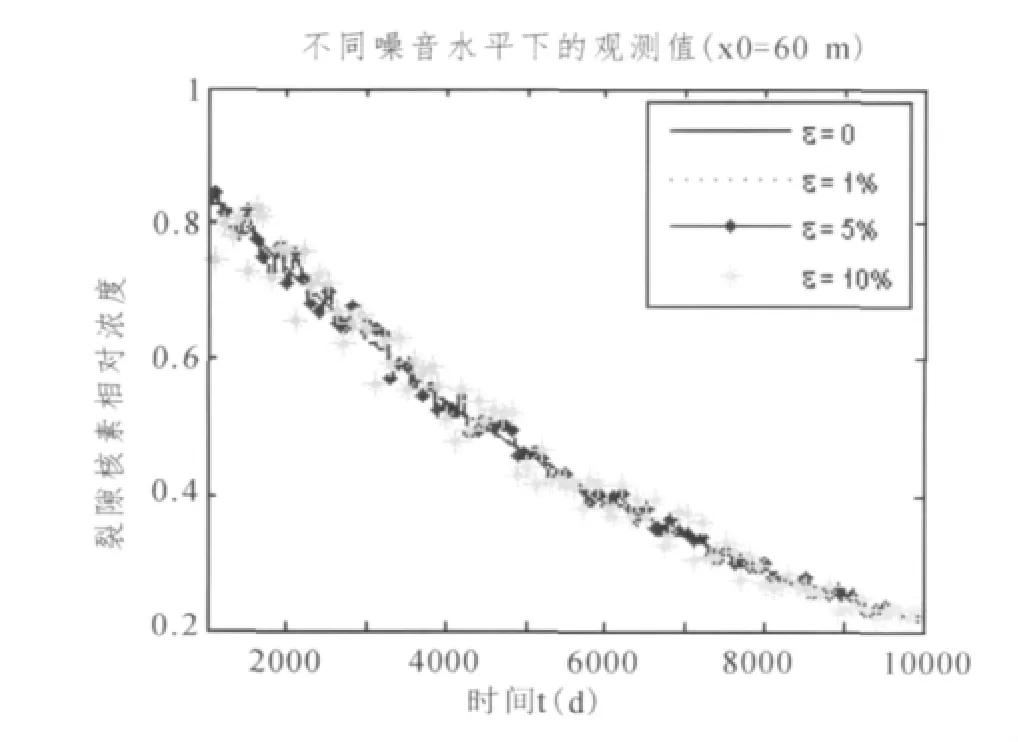
图6 不同噪音水平下的观测数据(x0=60 m)Fig.6 The observed data under different noise levels(x0=60 m)

针对二维单裂隙-孔隙双重介质系统中的核素迁移耦合问题，利用Fourier变换方法与Saul’yev不对称差分格式得到正问题的解;另一方面，首先将参数反演反问题归结为一等价的泛函极小化问题，然后利用遗传算法经过交叉、选择和变异等步骤得出反问题的解。从算例的计算结果可以看出，正问题的解析解能较好地刻画核素的迁移规律;遗传算法也能有效地实现单裂隙-孔隙双重介质耦合模型地质参数的反演。对于有效地反演多裂隙以及三维裂隙-孔隙双重介质系统的迁移问题，需要展开更深入的研究。

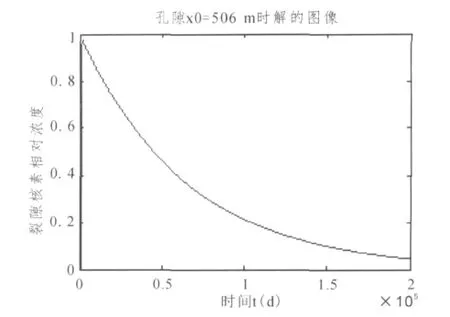
图5 单裂隙中所含核素迁移规律(x0=506 m)Fig.5 Migration of nuclides contained in a single fracture(x0=506 m)

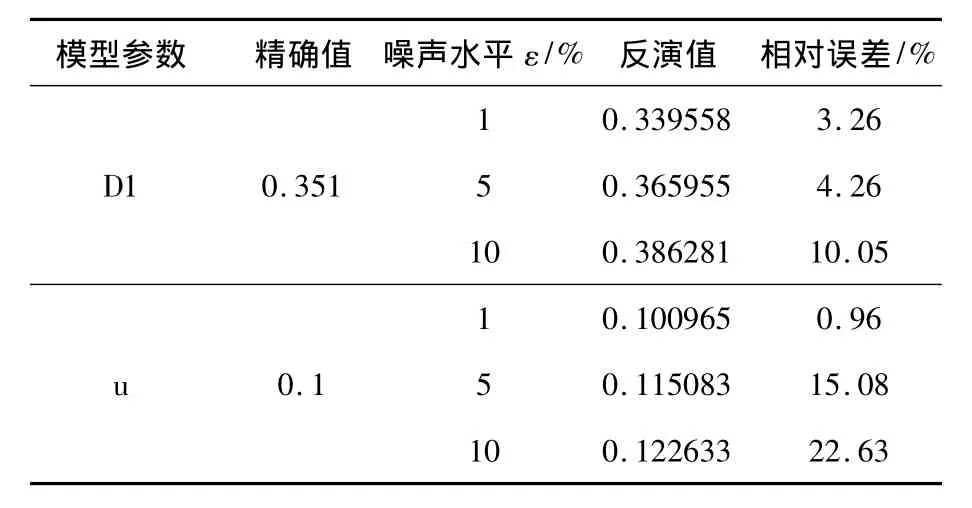
表1 x0=60 m时参数反演结果Tab.1 The inversion results of the two parameters under different noise levels(x0=60 m)

顾正华.2006.广义遗传算法及其在水流参数反演中的应用[J].系统工程理论与实践，26(2):133-137.

郭敏丽，王金生，李书绅.2004.饱和黄土中3H和Br－迁移的延迟特征[J].环境科学学报，24(5):878-882.

李金轩，李寻.2001.基于双重介质理论的单裂隙核素迁移模型[J].勘察科学技术，2:7-11.

李录，李春江，张吴平.1998.单裂隙花岗岩中核素迁移的连续数学模型研究[J].山西大学学报:自然科学版，21(1):1-9.

李寻，张土乔，李金轩.2010.单裂隙介质中核素迁移模型的解析解及其应用[J].哈尔滨工业大学学报，42(12):1990-1994.

梁冰，刘磊.薛强，等.2007.核素渗漏对地下水污染的数值仿真研究[J].系统仿真学报，19(2):261-263.

刘建国，聂永丰.2001.非饱和土壤水力参数预测的分形模型[J].水科学进展，12(1):99-106.

刘金英，王新民，彭泽洲.1996.双重介质中核素迁移模型的解析解及其应用[J].世界地质，15(1):68-73.

刘晓丽，梁冰，薛强，等.2003.多孔介质渗透率的分形描述[J].水科学进展，14(6):769-773.

罗嗣海，钱七虎，李金轩，等.2005.高放废物深地质处置中的多场耦合与核素迁移[J].岩土力学，26(Z1):264-270.

马应明，金玉仁.2007.钚在地下水中的存在形态分析[J].东华理工学院学报，30(3):236-240.

闵涛，周孝德，张世梅，等.2004.对流－扩散方程源项识别反问题的遗产算法[J].水动力学研究与进展(A辑)，19(4):520-524.

王青海，王兰生，李晓红.2004.基岩裂隙水中90Sr迁移的数值模拟[J].吉林大学学报，34(3):405-409.

王榕树，冯为.1994.放射性核素在地质介质中的迁移研究[J].核化学与放射化学，16(2):117-121.

王彦飞.2007.反演问题的计算方法及其应用[M].北京:高等教育出版社.

王泽文，邱淑芳.2008.一类流域点污染源识别的稳定性与数值模拟[J].水动力学研究与进展(A 辑)，23(4):364-371.

仵彦卿.2007.多孔介质污染物迁移动力学[M].上海:上海交通大学出版社.

谢运棉，杨天行，王运国等.1992.放射性核素在裂隙岩石中的迁移模型研究[J].岩石学与工程学报，11(1):1-24.

杨巍，杨亚新，曹龙生，等.2011.某铀尾矿库中放射性核素对环境的影响[J].东华理工大学学报:自然科学版，34(2):231-235.

杨勇，苑国琪，张东.2004.90Sr，137Cs在某种包气带土壤中的迁移研究[J].四川环境，23(3):85-89.

郁伯铭.2003.多孔介质输运性质的分形分析研究进展[J].力学进展，33(3):333-346.

张东辉，施明恒.2003.多孔介质扩散、导热、渗流分形模型的研究[D].南京:东南大学.

张文，王泽文，乐励华.2010.双重介质中的一类核素迁移数学模型及其反演[J].岩土力学，31(2):553-558.

张文生.2006.科学计算中的偏微分方程有限差分法[M].北京:高等教育出版社.

中国人民解放军总装备部军事训练教材编辑工作委员会.2002.地下核爆炸现象学概论(下册)[M].北京:国防工业出版社.

Ahsanuzzaman A，Kolar R，Zaman M.2003.Limiting Source Dimensions of Three-Dimensional Analytical Point Source Model for Solute Transport[C].Hydrology Days Proceedings:1-15.

Pollner L，Zagyvai P.1999.Subsurface transport modeling of longlived nuclides[J].Waste Management，19:45-54.

Zhang L X，Zhang M S.Tu G R.1995.A field study of tritium migration in groundwater[J].The Science of the Total Environment.173/174:47-51.

Gastberger M，Steinhausler F，Gerzabek M H，et al.2000.Soil-toplant transfer of fallout caesium and strontium in Austrian lowland and Alpinepastures[J].J.Environ Radioactivity，49:217-233.

Borje T.1986.Migration of the fission products strontium.tech-netium.lodine and cesium in clay[J].Radiochim Acta，39:97-104.

Burnett W C.2001.Elzerman A W.Nuclide migration and theenvironmental radiochemistry of florida phosphogyp sum[J].J Environ Radioactivity，54:27-51.

Hatano Y，Hatano N，Amano H.et al.1998.Aerosol migration near chernobyl:longterm data and modeling[J].A tmospheric Environment，32(14-15):2587-2594.