本原不可幂几乎可约定号有向图的 k重下广义基✳

沈佳煜,高玉斌

(中北大学 理学院,山西 太原 030051)

0 引 言

一个实数 a的符号记为 sgn a,根据a＞0,a＜0或a=0,它们的符号分别定义为1,-1或0.一个实矩阵A的符号模式是将 A中的所有元素都换成它的符号后所得的符号矩阵,记为sgn(A).在文献 [1]中引入了一个新的符号 #来表示正负相加所得的未定元,集合Γ={1,-1,0,#}定义为广义符号集,运算法则如下:

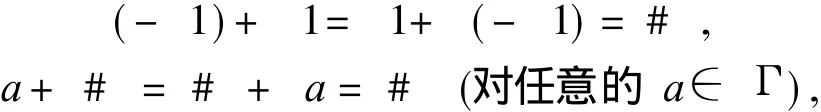
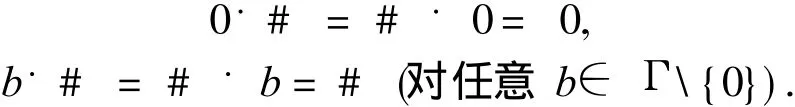
设A=(aij)是一个n阶符号模式矩阵,A的伴随有向图 D(A)(可能含有环)是顶点集 V={1,2,… ,n}和弧集 E={(i,j)|aij≠0}的有向图,按照 A中 aij的符号,将 D(A)中的每一条弧分别规定符号所得的图称为 A的伴随定号有向图,表示为 S(A).因此符号模式矩阵和定号有向图之间存在一一对应的关系.本文中的一些定义、引理和文献,一部分是从符号模式矩阵去描述基或本原指数的性质,一部分是从定号有向图去描述基或本原指数的性质等,当哪个方面更有助于研究就从哪个方面去入手,其本质上都是一样的.

设 A是非负矩阵,若存在正整数 k,使得Ak＞0,则称 A是本原矩阵.设 A是一个n阶符号模式矩阵,A,A2,A3,… 是A的幂,假定Al是序列中第一个重复的幂,即假定 l是最小的正整数且有一个最小的正整数 p使得 Al=Al+p,则称l为A的基,用 l(A)表示.如果 A的每次幂都不包含# 元素,则称 A为可幂的;如果 A是本原的,则 S(A)也是本原的;若是 A可幂的,则S(A)也是可幂的.

一条定号有向图中的途径 W是由一些弧有序排列成的,e1,e2,… ,ek,其中 ei的终点和 ei+1的起点相同,i=1,…,k-1,k是 W的长度,记为l(W).途径的符号定义为sgn W.一个定号有向图的两条途径 W1和 W2被称为 SSSD途径对,如果他们有相同的起点和终点,长度相同,符号相反.

D是 V(D)={1,2,… ,n}的本原图,设 X⊆V(D),那么 exp(D,X)是指最小的整数 m使得D中每个顶点 i,从 X中的一些顶点到 i存在长度为 m的途径.

定义 1[2]设 D是一个 n阶本原图且 1≤k≤n,那么 f(D,k):=min{exp(D,X)|X⊆V(D),|X|=k}称为 k重下本原指数.

设 S是一个 n阶本原不可幂定号有向图,设u,v∈V(S),若存在正整数 l,使对每一个整数t≥l,总存在一个从 u到 v长为 t的 SSSD途径对,则最小的整数 l就称为从 u到 v的基,记为l S(u,v).设 u∈ V(S),若存在正整数 l,使对每一个整数 t≥l,总存在一个从 u到 v(v∈ V(S))长为 t的 SSSD途径对,则最小的整数 l就称为顶点 u的基,记为 lS(u).

定义 2[3]设 S是一个 n阶本原不可幂定号有向图,V(S)={v1,v2,…,vn},把 S中的顶点按照 l S(v1)≤lS(v2)≤…≤lS(vn)的顺序排列,其中l S(vk)称为 S的第 k个 local基,记为 lS(k),1≤ k≤ n.

对于一个子集 X⊆V(S)且 |X|=k(1≤k≤n),定义 X的基为使得对每个顶点 v∈ V(S),从X中的一些顶点到 v有一对长度为 p的 SSSD途径对的最小的整数 p,记为 lS(X).L(S,k)=max{lS(X)|X⊆V(S)且 |X|=k}称为 S的 k重上广义基.

定义 3[4]设 S是一个 n阶本原不可幂定号有向图,k是一个整数,1≤k≤n,那么 S的 k重下广义基是 j(S,k)=min{l S(X)|X⊆V(S)且|X|=k},显然 j(S,1)≥…≥j(S,n).

本文研究了本原不可幂几乎可约定号有向图(也就是本原不可幂几乎可约符号模式矩阵)的 k重下广义基,得到了本原不可幂几乎可约定号有向图的 k重下广义基的界,刻划了一些情况下界的等式.设 Dn-1,s是图1中给定的 n阶本原不可幂几乎可约定号有向图.

图1 图 Dn-1,s(n≥ 7,s≤n-1)Fig.1 Dn-1,s(n≥ 7,s≤ n-1)digraph

1 预备知识

引理 1[5]如果 S是一个本原不可幂的定号有向图,那么 S中存在两个不同的圈分别是 C1,C2(长度分别为 p1和 p2)满足下面的两个条件之一:① pi是奇数,p j是偶数,并且有 sgn Cj=-1(其中 i,j=1,2并且 i≠j).② p 1和 p 2都是奇数,并且有 sgn C1=-sgn C2.称满足 ①或②的圈对 C1和 C2为异圈对.若 C1和 C2是长度分别为 p 1和 p2的异圈对,则闭途径 W1=p2C1和 W2=p1C2有相同的长度 p1p2,但有不同的符号(sgn(C1))p2=-(sgn(C2))p1.

引理 2[6]设 D是 n阶本原图,且包含两个长度分别为 s和 s+ 1的圈,则对于 k＜s,有

引理 3[6]设 D是 n阶本原图,L(D)是 D中的圈长集合,L(D)={s,s+2},且 D仅有两个圈,如果 k＜s,那么

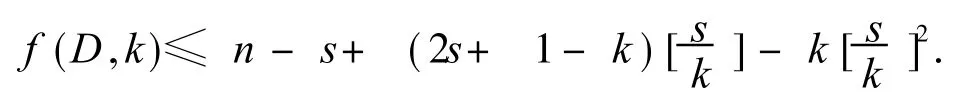
引理 4[4]设 S是 n阶本原不可幂定号有向图,D是它的基础有向图,令 W1和 W2是从顶点u到 v的长度为 r(S)的 SSSD途径对,d(S)表示 S的直径,则对于 1≤k≤n,有

引理 5[4]设 S是 n阶本原不可幂定号有向图,则j(S,1)=l S(1),j(S,n)=L(S,n).

假定 a1,… ,ak是正整数,g.c.d(a1,… ,ak)=1,定 义 Frobenius集 合 S(a1,…,ak)={r1a1+…+ rkak|r1,…,rk是非负整数 },定义Frobenius数 h(a1,…,ak)是最小的的正整数 h,使得任何整数 m≥h,都有 m∈ S(a1,… ,ak)成立,显然 h(a1,… ,ak)-1∉ S(a1,… ,ak).若 g.c.d(a,b)=1,则h(a,b)=(a-1)(b-1).

引理 6[7]设 D是本原图(如图2所示),1≤k≤n,X是 D中的顶点的集合,|X|=k,那么对于任意整数 l≥ (n-k)(n-1)和任意顶点 i(其中1≤i≤n-1),从一些顶点 x0∈ X到 i存在长度为l的路径.

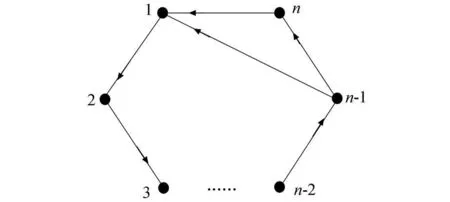
图2 n阶本原图 Dn,n-1Fig.2 Primitiv e digraph of order n Dn,n-1

引理 7[8]设 D是图 Dn-1,n-2,当 1≤k≤n-2时,lS1(k)= 2n2-8n+ 9+ k.设 D是图Dn-1,n-3,当 1≤k≤n-3时 ,l S1(k)=2n2-10n+13+k.

2 主要结果

定理 1 设 S1是本原不可幂几乎可约定号有向图,Dn-1,n-2是它的基础有向图;设 S2是本原不可幂几乎可约定号有向图,Dn-1,n-3是它的基础有向图.则对于 1≤k＜n-2,有

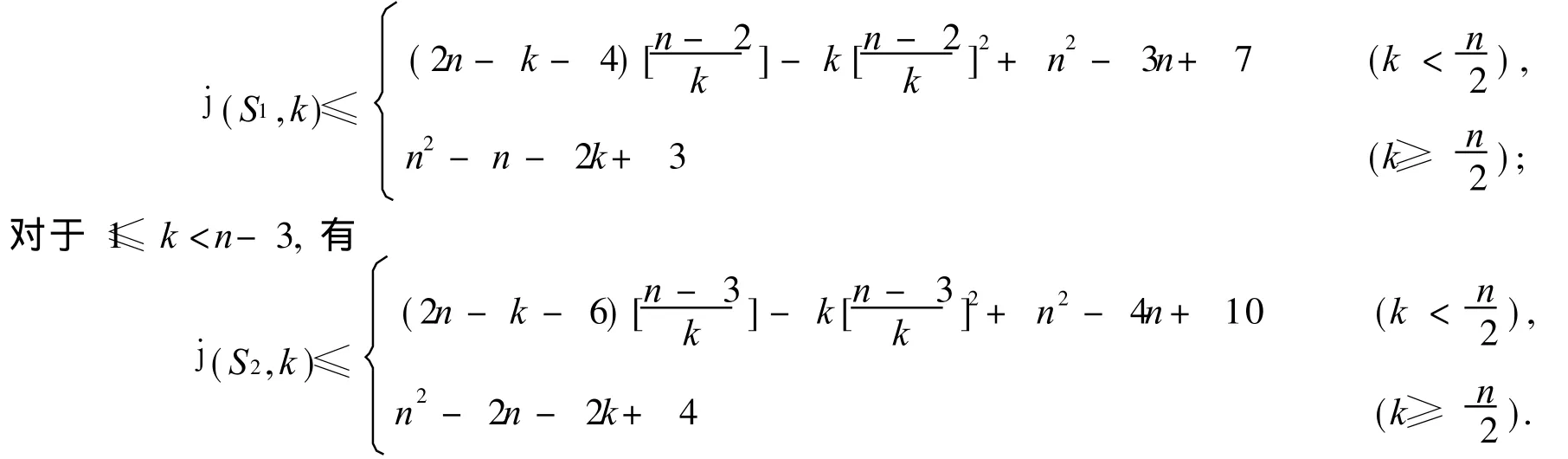
证明 注意到 S1只有两个长度分别为 n-1和 n- 2的圈 Cn-1和 Cn-2,根据引理 1,有sgn((n-1)Cn-2)=-sgn((n-2)Cn-1).

令 Q1和 Q2是从 1到 n-3长度分别为 2和 3的途径,且 P是从 n-3到 1的唯一途径.设W1=Q1+(n-2)Cn-2和 W2=Q2+(n-3)Cn-1,则l(W1)=l(W2),W1+P=(n-1)Cn-2,W2+P=(n-2)Cn-1,因此 sgn(W1+P)=-sgn(W2+P),即 sgn(W1)=-sgn(W2),所以 W1和 W2是从 1到 n-3的一对长度为 n2-4n+6的 SSSD途径对.因此

当 1≤k＜n-2时,根据引理 2和引理 4得j(S1,k)≤ f(Dn-1,n-2,k)+ r(S1)+ d(S1)≤

S2中只有两个长度分别为 n-1和 n-3的圈Cn-1和 Cn-3,根据引理 1,有

sgn((n- 1)Cn-3)=- sgn((n- 3)Cn-1),从 1到 n-4有长度为 n2-5n+8的 SSSD途径对.

当 1≤k＜n-3时,根据引理 3和引理 4得

定理 2 设 S1是 n阶本原不可幂几乎可约定号有向图,Dn-1,n-2是它的基础有向图,则

证明 首先,根据定理 1可以知道从顶点 1到 n-3有一对长度为 n2-4n+6的 SSSD途径对.设 y是 S1中的任意一个顶点,P是从 n-3到y的最短途径,l(P)≤n-2.定义 q=-(n-2)+n+n-2-l(P),则 q≥-(n-2)+n,根据引理6,从一些顶点 x0∈ V(S1)到 1存在一条长度为 q的途径 Q,因此 Q+W1+P和 Q+W2+P是从 x0到 y的长度为 n2-3n+6的 SSSD途径对,所以j(S1,n)≤n2-3n+6.

另一方面,证明从 S1中的任何顶点到 n没有长度为 n2-3n+3的 SSSD途径对.

情况 1 假定 W1和 W2是两条从顶点 m到 n的长度为 n2-3n+3的途径,1≤m≤n-2,则每个 Wi是由从 m到 n一条长度为 m的路及若干的n-1圈和 n-2圈组成,因此存在非负整数 ai,bi(i=1,2)且 a2≥a1,b1≥b2,使得 n2-3n+ 3=ai(n-1)+bi(n-2)+m(i=1,2),从此可以得到h(n-1,n-2)-1=(n-2)(n-3)-1=(a2+mn)(n-1)+(b2+n-m-1)(n-2).注意到 (a2-a1)(n-1)=(b1-b2)(n-2),可得 (n-2)|(a2-a1).如果 a1≠a2,则 a2＞ a1+n-2,因此 a2+mn≥a1+n-2+m-n=a1+m-2≥ 0.当 m≥ 2时 ,a2+m-n≥0成立;当 m=1时,因为是从顶点 1到 n,而这两个顶点都在 n-1圈里,所以 a1≥1,即 a2+m-n≥0依然成立.另外由于 m≤n-1,则 b2+n-m-1≥0,这样就矛盾于 h(n-1,n-2)的定义.

情况 2 当 m=n-1时,h(n-1,n-2)-1=(n-2)(n-3)-1=a2(n-1)+b2(n-2)-n=(a2-2)(n-1)+ (b2+ 1)(n-2),根据情况 1,a2≥a1+n-2,n-1和 n这两个顶点都在 n-1圈里,所以 a1≥ 1,因此 a2≥n-1,即 a2-2≥ 0.这样就矛盾于h(n-1,n-2)的定义.

情况 3 当 m=n时,h(n-1,n-2)-1=(n-2)(n-3)-1=a1(n-1)+(b1-1)(n-2).注意到 (a2-a1)(n-1)= (b1-b2)(n-2),可得(n-1)|(b1-b2).如果 b1≠b2,则有 b1-1+b2+n-2≥ 0,矛盾于 h(n-1,n-2)的定义.

所以 a1=a2且 b1=b2,即有 sgn(W1)=sgn(W2),矛盾于 SSSD途径对的定义.这就证明了对于在 S1中从顶点 m到 n不存在长度为n2-3n+3的 SSSD途径对,所以j(S1,n)≥n2-3n+4.至此,定理得证.

定理 3 设 S1是 n阶本原不可幂几乎可约定号有向图,Dn-1,n-2是它的基础有向图,则

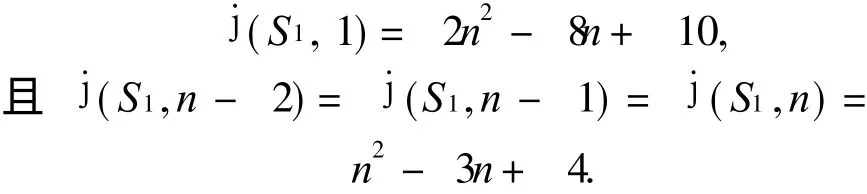
证明 根据引理 5和引理 7,可以直接算得j(S1,1)=lS1(1)=2n2-8n+ 10.

现在证明j(S1,n-2)=n2-3n+4.设 Cn-2和是长度分别为 n-2和 n-1的圈.

首先证明从 i+1到 i(1≤i≤n-3)有一条长度为 n2-3n+3的 SSSD途径对.取=(n-1)+ (i+ 1,i)和= (n-2)+ (i+ 1,i),这里 (i+1,i)表示从 i+1到 i的唯一途径,则-(i+ 1,i)=(n-1)Cn-2,-(i+ 1,i)=(n-2).由于 S1是不可幂的,和 Cn-1是S1仅有的两个圈,则 Cn-2和 Cn-1肯定是异圈对,因此 (n-1)Cn-2和 (n-2)Cn-1的符号不同,即和有不同的符号,所以从 i+ 1到 i有一条长度为 n2-3n+3的 SSSD途径对.设 X={1,2,…,n-2},因此 |X|=n-2.取 W1=(n-1)Cn-2+ (1,n-2)+ (n-2,n-3)和W2=(n-2)Cn-1+(1,n-2)+ (n-2,n-3),那么 W1和 W2是从 1到 n-3长度为 n2-3n+4的 SSSD途径对;取 W1=(n-1)Cn-2+ (1,n-2)和 W2=(n-2)+ (1,n-2)是从 1到 n-2长度为 n2-3n+3的 SSSD途径对,取 W1=(n-1)Cn-2+(1,n)+(n,n-1)和W2=(n-2)Cn-1+ (1,n)+(n,n+1)是从 1到 n-1长度为 n2-3n+4的途径对,取 W1=(n-1)Cn-2+ (1,n)和 W2=(n-2)Cn-1+(1,n)是从 1到 n长度为 n2-3n+ 3的途径对,因此 j(S1,n-2)≤n2-3n+4.

另一方面,由定理 2可知从顶点 k(1≤k≤n)到顶点 n没有长度为 n2-3n+3的 SSSD途径对,这表明j(S1,n-2)≥n2-3n+4.综上所述,j(S1,n-2)=n2-3n+ 4,再由定义 3和定理 2,j(S1,n-2)≥j(S1,n-1)≥j(S1,n)≥ n2-3n+4.

定理得证.

定理 4 设 S2是本原不可幂几乎可约定号有向图,Dn-1,n-3是它的基础有向图,因此

证明 从顶点 1到 n-4有一对长度为 n2-5n+8的 SSSD途径对.设 y是 S2中的任意一个顶点,P是从 n-4到 y的最短途径,l(P)≤n-2;定义 q=-(n-3)+n+n-2-l(P),则 q≥-(n-3)+n.从一些顶点 x0∈ V(S2)到 1存在一条长度为 q途 Q,因此 Q+W1+P和 Q+W2+P是从 x 0到 y的长度为 n2-4n+9的 SSSD途径对.所以

j(S2,n)≤n2-4n+ 9.另一方面,设 X 0={n,n-1,…,1},使得|X 0|=n.证明从 X 0的任意顶点到n-2没有长度为 n2-4n+5的 SSSD途径对.

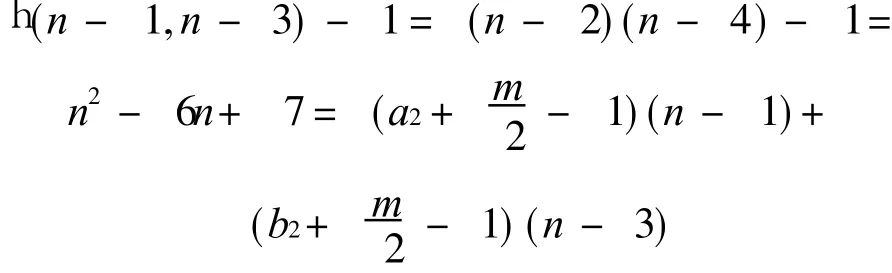
情况 1 当 1≤m≤n-3时,设 W1和 W2是两条从顶点 m到 n-2的长度为 n2-4n+5的SSSD途径,则每个 Wi是由一条从 m到 n-2长度为 m+2的路及若干的n-1圈和 n-3圈组成,因此存在非负整数 ai,bi(i= 1,2)且 a2≥a1,使得n2-4n+5=ai(n-1)+bi(n-3)+m+ 2(i=1,2).从此可以得到当 m是偶数时成立,而且有这样就矛盾于 h(n-1,n-3)的定义,所以 a1=a2,得 sgn(W1)=sgn(W2),即 W1和 W2的符号相同,这与 SSSD途径对的定义相矛盾,这就证明了从 m(偶数)到 n-2没有长度为 n2-4n+5的 SSSD途径对.当 m是奇数时,可以设顶点为设 W1和 W2是两条从顶点 m到 n-2的长度为 n2-4n+5的SSSD途径,则每个 Wi是由一条从 m到 n-2长度为 m+2的路及若干的n-1圈和n-3圈组成,因此存在非负整数 ai,bi(i=1,2)且 a2≥a1,使得

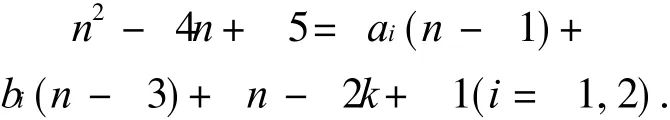
从此可以得到

因为

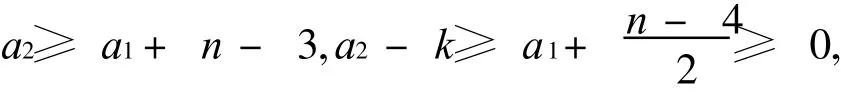
这样就矛盾于h(n-1,n-3)的定义,所以 a1=a2,得 sgn(W1)=sgn(W2),即 W1和 W2的符号相同,这与 SSSD途径对的定义相矛盾,这就证明了从 m(奇数)到 n-2没有长度为 n2-4n+5的SSSD途径对.

情况 2 当 m=n-2时,设 W1和 W2是两条从顶点 n-2到 n-2的长度为 n2-4n+ 5的SSSD途径,则每个 Wi是由一条从 n-2到 n-2长度为 0的路及若干的 n-1圈和 n-3圈组成,因此存在非负整数 ai,bi(i=1,2)且 a2≥a1,使得n2-4n+ 5=ai(n-1)+bi(n-3)-2n+ 4(i=1,2).从此可以得到

且 a2-1≥0,b2-1≥0,这样就矛盾于 h(n-1,n-3)的定义,所以 a1=a2,得 sgn(W1)=sgn(W2),即 W1和 W2的符号相同,这与 SSSD途径对的定义相矛盾,这就证明了从 n-2到 n-2没有长度为 n2-4n+5的 SSSD途径对.

情况 3 当 m=n-1时,设 W1和 W2是两条从顶点 n-1到 n-2的长度为 n2-4n+ 5的SSSD途径,则每个 Wi是由一条从 n-1到 n-2长度为 1的路及若干的 n-1圈和 n-3圈组成.取W1=(n-1)Cn-3+n和W2=(n-3)Cn-1+n,W1和 W2是从顶点 n-1到 n-2最短的 SSSD途径;又因为 W1=W2=n2-3n+3＞n2-4n+5,所以从 n-1到 n-2没有长度为 n2-4n+ 5的SSSD途径对.

情况 4 当 m=n时,设 W1和 W2是两条从顶点 n-1到 n-2的长度为 n2-4n+5的 SSSD途径,则每个 Wi是由一条从 n-1到 n-2长度为 1的路及若干的 n-1圈和 n-3圈组成,因此存在非负整数 ai,bi(i=1,2)且 a2≥a1,使得 n2-4n+5=ai(n-1)+bi(n-3)-2n+6(i=1,2).从此可以得到

这样就矛盾于h(n-1,n-3)的定义,所以 a1=a2,得 sgn(W1)=sgn(W2),即 W1和 W2的符号相同,这与 SSSD途径对的定义相矛盾,这就证明了从 n到 n-2没有长度为 n2-4n+5的 SSSD途径对.

定理 5 设 S2是本原不可幂几乎可约定号有向图,Dn-1,n-3是它的基础有向图,则

证明 根据引理 5和引理 7,可以得出j(S2,1)=l S2(1)=2n2-10+ 14.

现在来证明j(S2,n-2)=n2-4n+6.设Cn-3和 Cn-1是长度分别为 n-3和 n-1的圈.首先证明从 i+ 1到 i(1≤i≤n-4)有一条长度为 n2-4n+4的 SSSD途径对.取 W(i)1=(n-1)Cn-3+(i+ 1,i)和= (n-3)+ (i+ 1,i),这里(i+ 1,i)表示从 i+ 1到 i的唯一途径,则 W(i)1-(i+ 1,i)= (n- 1)Cn-3,W(i)2-(i+ 1,i)= (n-3)Cn-1.由于 S2是不可幂的,和是 S2仅有的两个圈,则 Cn-3和 Cn-1肯定是异圈对,因此(n-1)Cn-3和 (n-3)Cn-1的符号不同,即 W(i)1和有不同的符号,所以从 i+1到 i有一条长度为 n2-4n+ 4的 SSSD途径对.设 X={1,2,…,n-2},|X|=n-2,取W1=(n-1)Cn-3+(1,n-3)+ (n-3,n-4)和W2=(n-3)+ (1,n-3)+(n-3,n-4),那么 W1和 W2是从 1到 n-4长度为 n2-4n+5的 SSSD途径对;取 W1=(n-1)+(1,n-3)和W2=(n-3)+(1,n-3)是从 1到 n-3长度为 n2-4n+4的途径对,取W1=(n-1)Cn-3+(1,n)+(n,n-1)+ (n-1,n-2)和W2=(n-3)Cn-1+ (1,n)+ (n,n-1)+(n-1,n-2)是从 1到 n-2长度为 n2-4n+6的途径对,取 W1=(n-1)Cn-3+ (1,n)+ (n,n-1)和 W2=(n-3)Cn-1+(1,n)+(n,n-1)是从 1到n-1长度为 n2-4n+5的途径对,取 W1=(n-1)Cn-3+ (1,n)和 W2= (n-3)Cn-1+ (1,n)是从1到 n长度为 n2-4n+4的途径对,因此 j(S2,n-2)≤n2-4n+6.由定义 3得

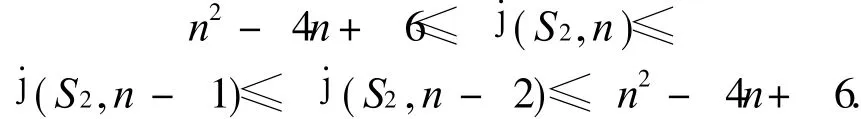
定理得证.

[1]Li Z,Hall F,Eschenbach C.On the period and base of a sign pattern matrix[J].Linear Algebra Appl.,1994,212/213:101-120.

[2]Brualdi R A,Liu Bolian.Generalized exponents of primitive directed graphs[J].Graph Theory,1990,14:483-499.

[3]Wang Longqin,Miao Zhengke,Yan Chao.Local bases of primitive non-powerful signed digraphs[J].Discrete Math.,2009,309:748-754.

[4]Liang Chaohua,Liu Bolian,Huang Yufei.The k th lower bases of primitive non-powerful signed digraphs[J].Linear Algebra Appl.,2010,432:1680-1690.

[5]You Lihua,Shao Jiayu,Shan Haiying.Bounds on the bases of irreducible generalized sign pattern matrices[J].Linear Algebra Appl.,2007,427:285-300.

[6]Liu Bolian, Huang Fengying. A conjecture about lower multiexponet of primitive matrices[J].Computers and Mathematics with Applications,2008,56:2100-2106.

[7]Shao Yanling,Shen Jian,Gao Yubin.The k th upper bases of primitive non-powerful signed digraphs[J].Discrete Math.,2009,309:2682-2686.

[8]Gao Yubin,Shao Yanling,Shen Jian.Bounds on the local bases of primitive nonpowerful nearly reducible sign patterns[J].Linear and Multilinear Algebra,2009,57:205-215.