H2控制在舰船主动隔振系统中的应用研究
2012-10-08邓文戈危建辉
邓文戈,颜 飞,危建辉
(海军广州地区装备修理监修室,广东广州510715)
0 引言
舰艇的振动和噪声不仅影响舰艇上人员的居住和工作环境,直接影响舰员身体健康,而且影响舰船上精密仪器设备的正常运行;更重要的是舰艇振动噪声水平直接影响舰艇技术性能,特别是对于潜艇来说,良好的减振降噪性能是增加其航行的稳定性和隐蔽性,提高战斗力的重要保障。浮筏隔振技术作为一种有效的隔振方式在船舶振动控制上已经广泛应用,其机理是利用浮筏装置中弹性元件的阻尼和中间质量来控制并衰减振动能量,其原理相当于双层隔振系统[1]。然而这种被动式的隔振方式对于低频振动,尤其是双层隔振装置自身固有频率附近的振动,难以进行有效隔离。主动控制技术利用外界能源以产生控制振动所需的作用力,实现被动技术无法实现的苛刻的减振要求。主动控制对控制算法具有较大的依赖性,因而不同的控制策略应用于浮筏双层隔振系统得到广泛研究[2,3]。理论上H2控制是求出全频率域上‖Tzw‖2最小化,因而其应用于主动隔振时,希望H2控制在低频段和被动系统固有频率区间有着良好隔振效果。本文采用不同的反馈变量,对双层隔振系统进行H2主动控制研究,通过分析输出目标和外界干扰激励的幅频特性,对控制策略进行评估,从而确定最佳方案。
1 H2控制律设计
控制系统框图如图1所示,图中P(s)是一个线性时不变系统,由以下状态空间描述:
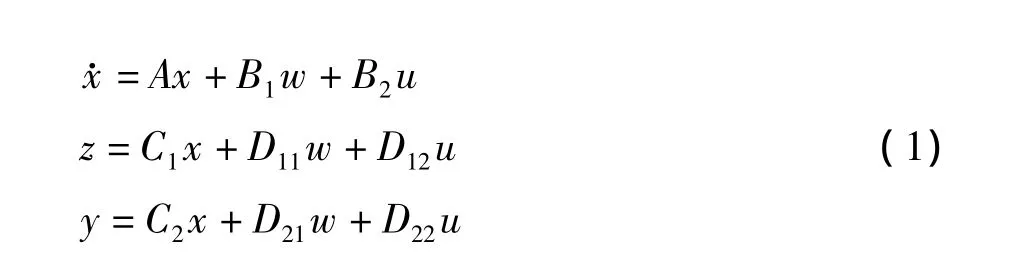
式中:x∈Rn是n维状态向量;u∈Rm是m维控制输入;y∈Rp是p维测量输出;z∈Rr是r维被调输出;w∈Rq是q维外部扰动,考虑外部扰动是不确定的,但是具有有限能量,即 w∈L2;A、B1、B2、C1、C2、D11、D12、D13、D22为对应维数矩阵;K(s)是所设计的控制器。
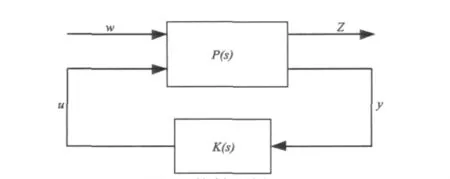
图1 控制系统框图
H2控制问题是求一个正则、实有理控制器K使得P(s)内稳定,且从外部扰动w到输出z的传递矩阵 Tzw的 H2范数最小[4]。
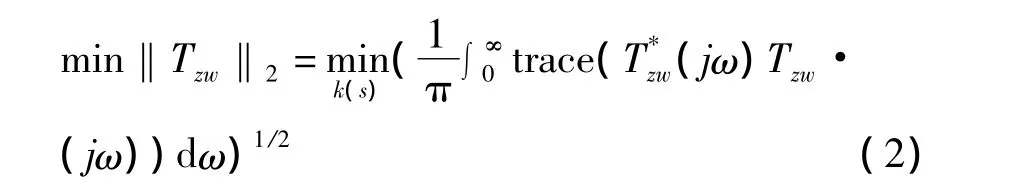
式中:jω为频率函数。
定理 1[4]对于给定的标量 γ>0,系统的 H2范数满足‖Twz(s)‖2<γ,系统存在状态反馈H2控制律,当且仅当存在对称正定矩阵X,Z和矩阵W,使得
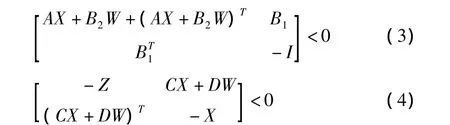

进而,如果上述矩阵不等式(3)、(4)和(5)存在一个可行解˜X,˜W,˜Z,则u=˜W(˜X)-1x是式(1)系统的一个状态反馈H2控制律。
式(3)中:I为单位矩阵。

2 双层隔振系统数学模型
双层隔振系统主动控制原理如图2所示,图中m1、x1为上层质量块质量与位移,m2、x2为中间质量块质量与位移,c1、k1为上层阻尼与刚度,c2、k2为下层阻尼与刚度,fu为作动器输出控制力,f为外界激励力。
式中:Hfz1、Hfz2分别为外界激励力与基座受力、控制器输出力之间的传递函数,通过分析不同控制反馈下Hfz1、Hfz2的幅频特性可得出外界激励与系统输出之间关系。
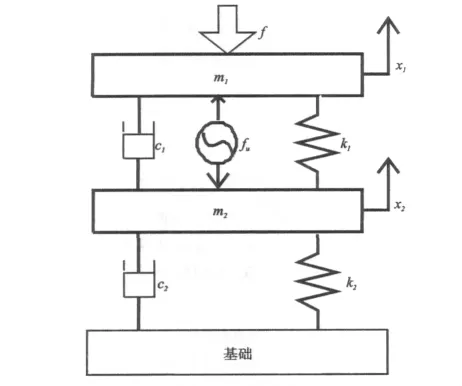
图2 双层隔振系统
3 仿真分析
双层隔振系统参数取m1=240 kg,m2=108 kg,c1=0 N·s/m,c2=0 N·s/m,k1=63 349 N/m,k2=101 720 N/m。选择不同的反馈控制变量,应用定理1确定控制器。双层隔振系统物理数学模型如下:式中:k2x2+c2x·2为传递到基座的力,反应隔振系统的隔振性能;fu为作动器输出控制力,作动器输出的力越大所需能量大小。

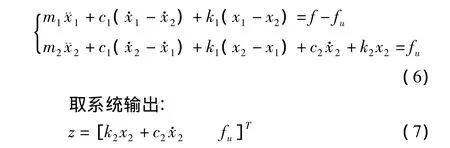
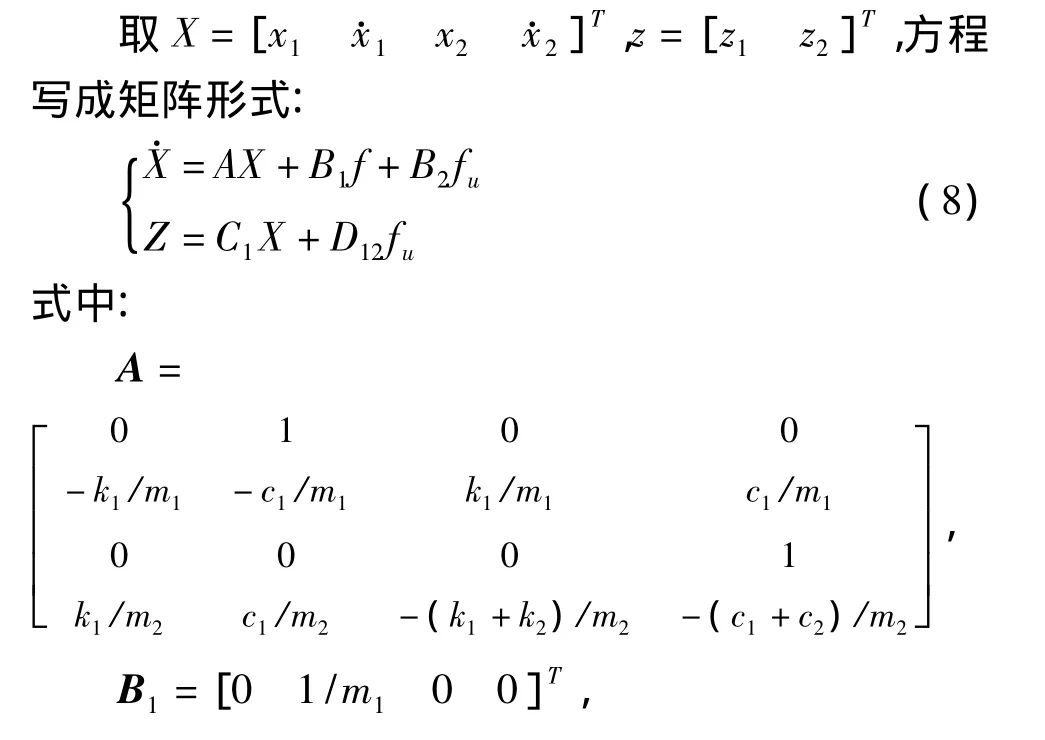
(4)采用全状态反馈时,应用matlab的LMI中的mincx命令解不等式组能方便求出不等式的最佳解,控制反馈K=105×[0.000 2 0.343 4 0.788 2-1.782 6],此时 trace(Z)<6.624 5 ×10-13。
各控制器确定后,可求出传递函数Hfz1、Hfz2,在不同反馈变量下Hfz1、Hfz2幅频特性曲线分别如图3、图4所示。通过分析幅频特性曲线可以求出不同反馈控制方式对系统输出性能的影响。
由图3Hfz1的幅频特性可知,采用上层质量和下层质量速度反馈在中低频段幅值明显小于被动隔振
系统,因而该频段内能起到很好的隔振效果,高频段幅值特性与被动隔振系统基本相同的,其中采用下层质量速度反馈隔振性能要好于上层质量速度反馈。而采用全状态反馈,对系统固有频率附近有着很好的隔振效果,但是频带较窄,高频段隔振效果不如被动隔振。采用基座力反馈,改变了系统的共振频率,基本上没有改善隔振效果。Hfz2的幅频特性如图4所示,反应作动器输出控制力与外界干扰力的比值。由图4可知采用上、下层质量速度反馈在超低频段所需力量大,即Hfz2幅值大于零,在高频段Hfz2幅值远远小于零,说明频率越高,所需控制力越小,从而所需外界能量越小,上层速度反馈高频效果越好;采用全状态反馈全频段Hfz2幅值较大,变化缓慢;采用基座输出力反馈,低频与全状态反馈基本相同,高频段Hfz2幅值衰减较快。综上所述,对双层隔振系统采用H2控制,并非反馈变量越多越好,速度反馈明显优于全状态反馈。
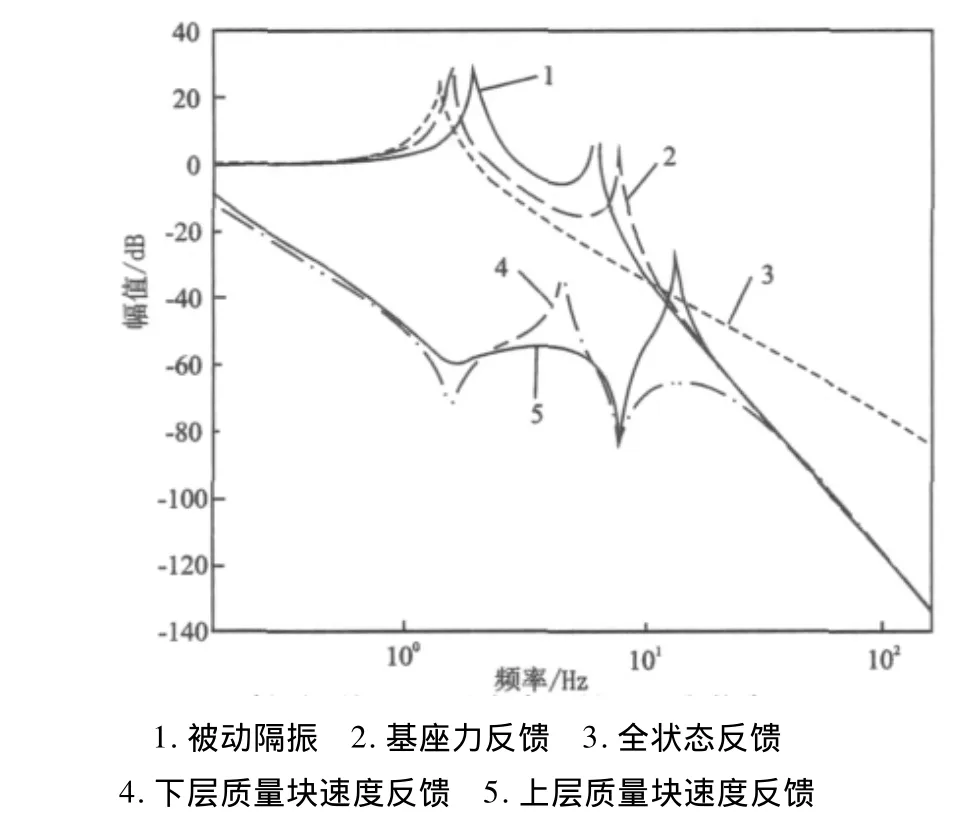
图3 传递函数Hfz1的幅频特性
4 结语
本文对双层隔振系统建立数学模型,提出系统关注输出目标;采用速度反馈、全状态反馈、输出目标反馈对双层隔振系统的H2控制策略进行了仿真研究;得到了各输出目标与外界激励力的幅频特性曲线。但文中所建立模型未考虑实际工程中的不确定性和不精确性,同时所得控制器阶数较高,因此控制方法的鲁棒性和控制器的降阶为下一步研究重点。
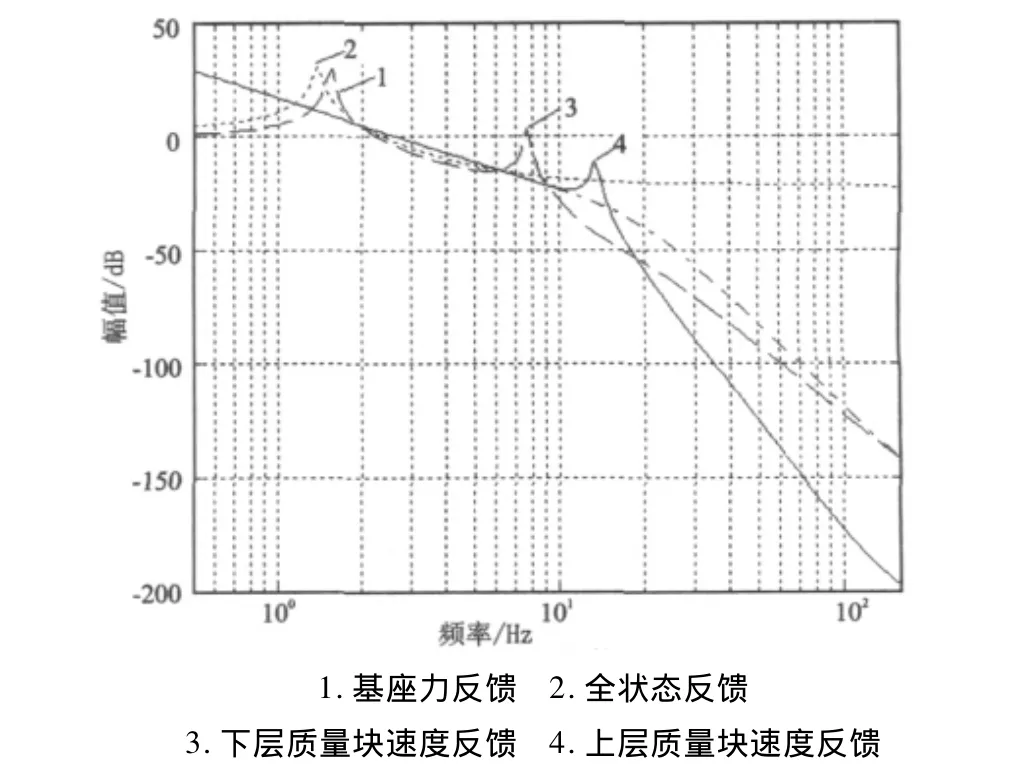
图4 传递函数Hfz2的幅频特性
[1] WENG Changjian.Recent Development in Field of Ship Vibration,Shock and Noise Research in China[J].Shipbuilding of China,2001,42(3):68-84.
[2] NIU J,SON G K,LIM C W.On active vibration isolation of floating raft system[J].Journal of Sound and Vibration,2005,285:391-406.
[3] 牛军川,宋孔杰.船载柴油机浮筏隔振系统的主动控制策略研究[J].内燃机学报,2004,22(3):252-256.
[4] 周克敏,Doly J C,Glover K.鲁棒最优控制[M].毛剑琴,钟宣生,林岩,译.北京:国防工业出版社,2006.
[5] 俞立.鲁棒控制-线性矩阵不等式处理方法[M].北京:清华大学出版社,2002.
