机载雷达对地动目标跟踪研究

唐 尧 杜自成 段芳芳 张 明 牟 聪

(西安电子工程研究所 西安 710100)

1 引言

工程上往往利用α-β滤波器进行航迹滤波以提高跟踪精度，然而试验发现对于已稳定跟踪的目标，若其突然发生运动状态的改变(如加速或减速等)，αβ滤波器的滤波误差容易发散。实际环境中，机载雷达所跟踪的地面目标(如坦克、战车等)其运动往往具有不确定的机动性。故而若直接对其进行α-β滤波，在强杂波背景下极其容易发生错误关联，导致航迹分叉或断航。为了克服发散问题，工程人员开发了衰减记忆滤波器［1］，它能有效减小与α-β滤波器有关的瞬时误差从而抑制滤波器发散。然而该滤波器实际是对目标跟踪点迹进行平滑作用，故而当滤波误差降低到一定程度后其滤波精度无法在点迹的累积过程中得到进一步改善。本文提出一种结合利用α-β滤波器和衰减记忆滤波器的滤波方法，使得机载雷达数据处理系统能够兼顾滤波器的跟踪精度和稳定性，从而实现对地面动目标的正确跟踪。

2 航迹起始问题研究

2.1 卡尔曼滤及α-β滤波器的滤波原理

雷达在对目标跟踪的过程中，由于受到其自身误差和目标机动性的影响，目标的探测值和预测值往往不能真实反应目标的运动状态。为了缩小雷达系统误差，实现对目标更为精确的跟踪，工程上往往利用α-β滤波器对雷达获取的数据信息进行滤波。而α-β滤波器本身是由卡尔曼滤波简化而来，下面就卡尔曼和α-β滤波器的工作原理进行描述。

卡尔曼滤波是将观测数据看成是某个用状态变量描述的系统输出，通过引入新息过程的概念，采用迭代方法利用观测数据进行运算，可以得到原系统状态向量的估计［2］。

卡尔曼滤波采用状态转移方程和量测方程来共同描述目标运动和雷达探测的过程。状态转移方程和量测方程表达式如下:

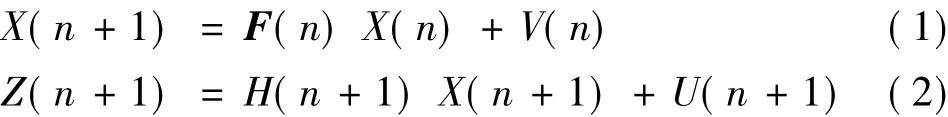
其中，X(n)和X(n+1)为系统在离散时间n时刻和n+1时刻的状态向量，Z(n)为系统在n时刻的观测向量。V(n)为过程噪声向量，它描述状态转移过程中的目标运动的变化;U(n)为观测噪声向量，它描述测量过程中的误差;V(n)和U(n)假设为为零均值的高斯白噪声。令矩阵Q(n)与R(n)是噪声V(n)和U(n)的协方差矩阵，则卡尔曼滤波的递推过程如下所示:

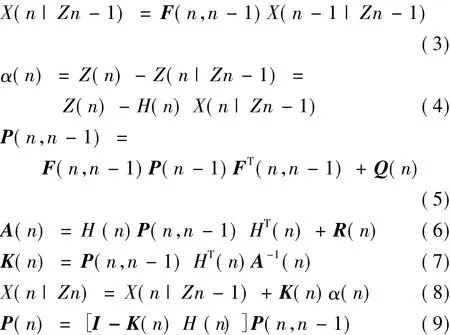
其中，α(n)为新息过程;P(n)为估计误差自相关矩阵;K(n)为增益矩阵;I为单位矩阵。卡尔曼滤波器的主要原理是利用过程噪声协方差矩Q(n)和观测噪声协方差矩阵R(n)两个参数共同描述待求状态向量的观测值和准确值之间的误差，从而一定程度上消除误差的影响，估计出待求状态向量的最优近似值［3］。

机载雷达受体积和费用的限制往往不希望在数据处理(以下简称数处)过程中引入太大的计算量从而扩大处理器硬件设备。而雷达对地面目标的跟踪过程中往往会搜索到大量目标，故而应当控制对单个目标跟踪的计算量。容易看出卡尔曼滤波器对增益矩阵K(n)的计算占了主要的工作量，为了减小计算量，可以改变增益矩阵的计算方法，为此提出了常增益滤波器。令δv和δw分别为过程噪声和量测噪声的标准差，增益矩阵K=［α β/T］T。α、β为定值的常增益系数，T为采样间隔。定义机动指标为:

将式(10)带入式(5)－(9)可得［4］

若过程噪声的标准差δv不能事先确定，那么λ就无法确定，工程上采用和时刻 n有关的 α、β确定方法［4］:

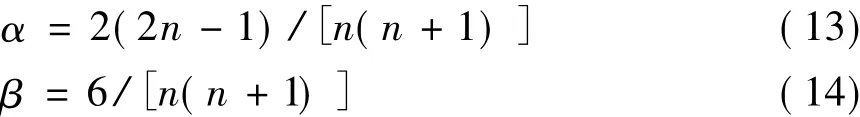
以雷达为圆心建立极坐标系，模拟目标距雷达20km，方位角30°，运动方向60°，速度大小为25m/s。将雷达探测坐标投影到大地坐标系下，令大地坐标系下雷达方位角误差为－0.5°～0.5°的均匀分布，距离误差为－5m～5m的均匀分布，扫描间隔为1s。

将如上雷达参数和目标参数设置定义为情形1，图1反应了对情形1进行500次Monte Carlo试验后x、y方向上目标真实位置和滤波位置的偏差随迭代步数累积的变化。

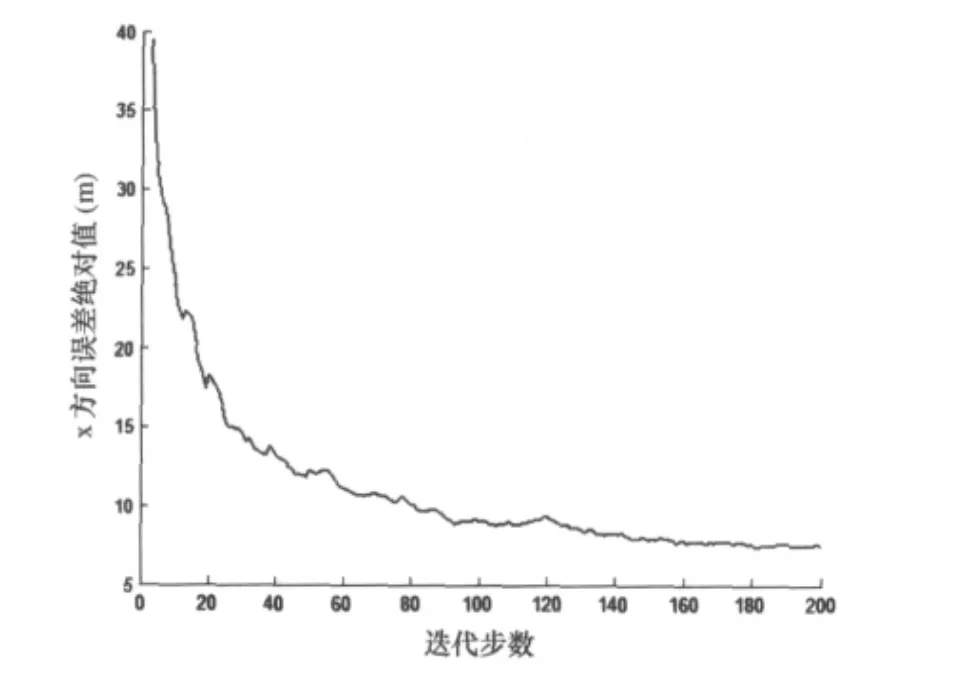
图1(a) x方向滤波误差

图1(b) y方向滤波误差

由图1可以看出滤波器误差随迭代步数的累积有收敛的趋势，因此若被跟踪目标在雷达跟踪时间内始终保持匀速运动则随着跟踪步数的累积能实现对目标的精确跟踪。

地面运动目标往往具有较高的机动性，极容易发生突然加速或突然减速的情况。而已进入稳定跟踪的目标其运动状态的改变会严重影响滤波效果。

设雷达参数和目标初始运动状态与上面设置相同，目标在98s开始以－4m/s2的加速度进行减速，减速3s后，以13m/s的速度匀速运动。

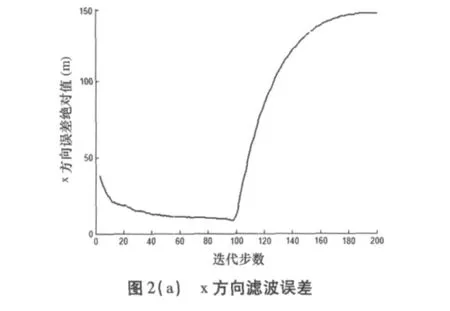
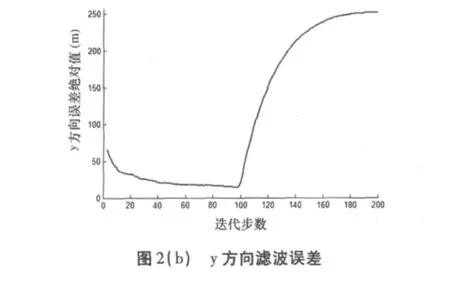
将如上雷达参数和目标参数设置定义为情形2，图2反应了对情形2进行500次Monte Carlo试验后，x、y方向上目标真实位置和滤波位置的偏差随迭代步数累积的变化。

由图2可以看出滤波器误差在迭代到100步后开始持续加大，即滤波发散。这是因为随迭代步数的累积，α和β的数值会逐渐减小，故而新息对滤波结果的影响会减弱。即当滤波器进入稳定跟踪后，滤波结果主要是由历史点迹估算出来的。因此若处于稳定跟踪阶段的目标其运动状态突然改变，则滤波器无法有效重新估计目标新的运动参数。

2.2 衰减记忆滤波器和α-β滤波器的比较

衰减记忆滤波器可以看作是一种特殊的α-β滤波器。定义ξ为平滑系数，0≤ξ≤1，令:

ξ趋近于0意味滤波器进行轻度平滑，ξ趋近于1意味着滤波器进行深度平滑。由式(15)、(16)知，衰减记忆滤波器的增益矩阵K(n)不随迭代步数n改变，因此新息对滤波器输出的影响是稳定的。

取平滑系数ξ=0.8。比较两种滤波器在情形1和情形2下的滤波效果。

图3为对情形1进行500次Monte Carlo试验后x、y方向上雷达探测目标位置、滤波位置与目标真实位置的偏差随迭代步数累积的变化。

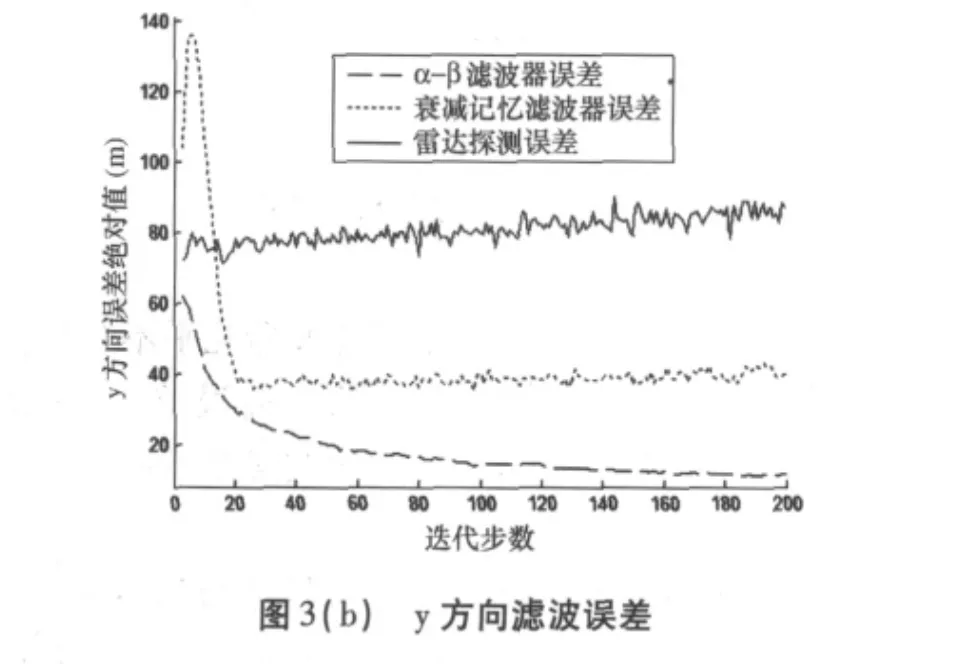
由图3可以看出雷达探测误差随迭代步数增加逐渐变大，这是因为目标朝远离雷达的方向运动其径向距离逐渐加大，故而在相同方位角误差的情况下其投影到x、y坐标轴上的误差也会加大。衰减记忆滤波器的滤波误差在跟踪起始阶段较大，这是因为此处选用了较大的平滑系数其不适于滤波精度较低的航迹起始阶段，迭代步数超过20步以后误差趋于收敛，收敛后随目标距离的渐远误差会有轻度的增加。比较3条误差曲线，可以发现对于情形1，αβ滤波器具有更好的滤波效果。

图4反应对情形2进行500次Monte Carlo试验后x、y方向上雷达探测目标位置及滤波位置与目标真实位置的偏差随迭代步数累积的变化。

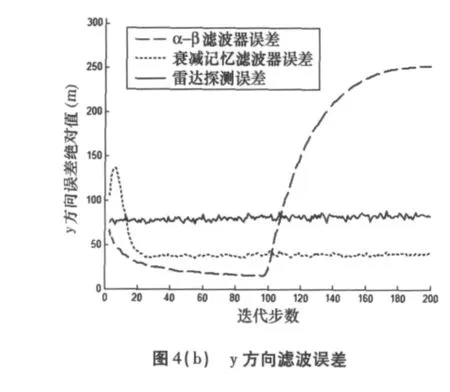
由图4可以看出衰减记忆滤波器几乎不受目标瞬时机动的影响，而保持恒定的滤波误差。α-β滤波器在目标发生瞬时机动后其滤波误差迅速加大以至发散。

2.3 α-β滤波器和衰减记忆滤波器结合利用方法

因为地面目标的加/减速过程往往是短暂而重复的，即目标在稳定行驶的过程中突然加速或减速，当切换到另一个速度后会保持该速度行驶一段时间，如此循环。为了兼顾滤波器的滤波精度和稳定性，一种可行的办法是在目标稳定行驶的时候利用α-β滤波器的滤波数据，而在目标发生瞬时机动的时段内采用衰减记忆滤波器的滤波数据。那么如何判断目标是否发生机动是问题的关键。自适应处理中往往利用新息作为目标机动的判据［5］，即若雷达对目标的探测位置和滤波位置间隔超过一定阈值(该阈值和目标距离及雷达测角精度有关)则认为目标运动状态改变。试验发现由于雷达误差的随机性，就单次试验而言若能保证对目标瞬时机动有较高的判决正确率，则该判决时刻相对于目标真实的运动状态改变时刻将有较大延时。

图5为对情形2的某次试验中，α-β滤波器和衰减记忆滤波器新息绝对值随迭代步数的改变。

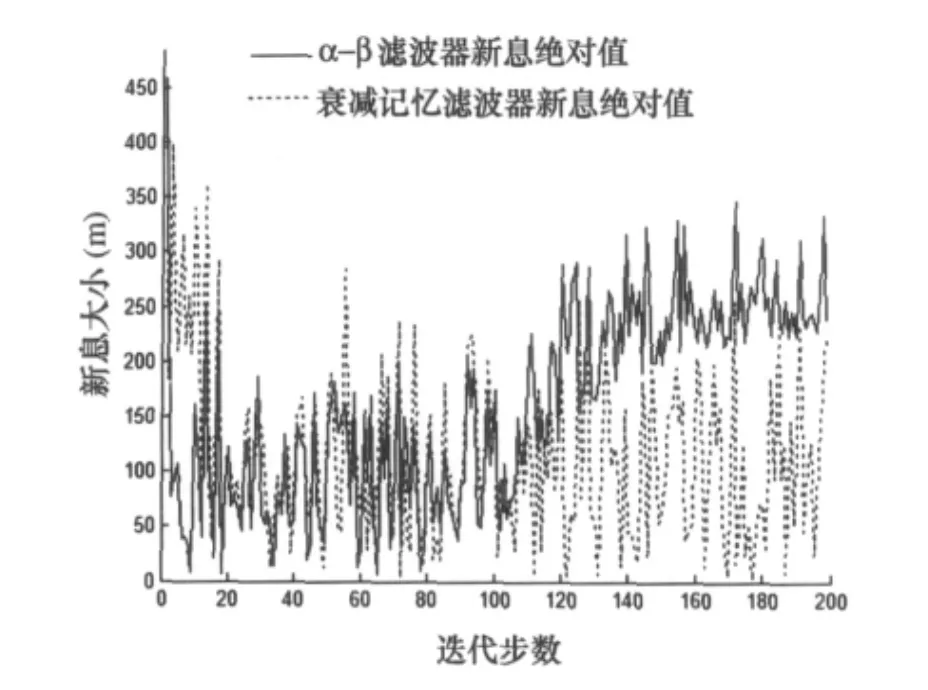
图5 新息随迭代步数积累的变化

由图5可以看出α-β滤波器新息迭代到115步以后才有明显变化，而实际目标加速发生在第98步到101步间。

为了减小雷达探测误差的随机性对目标运动状态改变判决的影响，可以利用滤波后的数据比较作为判决依据。令α-β滤波器n时刻的滤波位置为x1(n)和y1(n)，衰减记忆滤波器n时刻的滤波位置为x2(n)和y2(n)。令

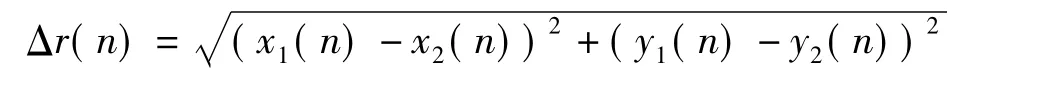
若Δr(n)＞ΔRmax则认为目标运动状态改变，ΔRmax为偏差门限，其大小与目标距离和迭代步数有关。

图6为对情形2的某次试验中，Δr(n)随迭代步数的变化曲线。

图6 滤波位置差随迭代步数积累的变化

由图6可看出迭代到103步时一定可以判决出目标运动状态的改变。虽然它滞后于目标实际的减速开始时刻，但由图4可看出在目标减速后，虽然α-β滤波器的滤波误差会逐渐加大，但在其加大的初期该滤波误差仍然要小于衰减记忆滤波器的滤波误差。

本文利用如下方法来结合α-β滤波器和衰减记忆滤波器对目标航迹进行滤波。

a.令雷达对目标的跟踪步数为n。当n≥3时，同时利用α-β滤波器和衰减记忆滤波器对目标航迹进行滤波，记滤波后的位置值分别为［x1(n)，y1(n)］和［x2(n)，y2(n)］。

b.对于跟踪起始阶段即n∈［3，20］，数处报出的目标位置为α-β滤波器输出滤波位置即［x1(n)，y1(n)］。

c.对于 n＞20的一次点滤波位置，计算 Δr(n)。若Δr(n)＜ΔRmax仍采用α-β滤波器输出的滤波位置;若检测到Δr(n)≥ΔRmax则认为目标运动状态发生改变，令此时刻为nb。

d.若判决运动状态已发生改变，将衰减记忆滤波器的前一步输出结果［x2(n－1)，y2(n－1)］带入α-β 滤波器;并令 nc=20，α =2(2nc－1)/［nc(nc+1)］，β =6/［nc(nc+1)］，将改变参数后的 α-β 滤波器的计算结果［x1(n)'，y1(n)'］作为数处报出结果。其后令 nd=nc+n－nb。将［x1(n－1)'，y1(n－1)'］带入 α-β 滤波器并令 α =2(2nd－1)/［nd(nd+1)］，β=6/［nd(nd+1)］，所得滤波位置 ［x1(n)'，y1(n)'］作为数处报出结果。利用改变参数的滤波器持续滤波m步后(此处令m=5)，再进行步骤c中的判决过程。

e.重复步骤c～d直到跟踪结束。

此处之所以在n=20以后才判决目标运动状态是否变化，是因为n较小时α-β滤波器对新息有较大的引入权重。即目标运动状态的改变发生在目标跟踪的初期并不会造成α-β滤波器误差的发散。之所以令nc=20是因为通过对不同雷达和目标参数选取的大量试验证明，n=20时α-β滤波器和衰减记忆滤波器的滤波误差统计结果最为接近。图2和图3的仿真结果证明了这一点。

3 仿真验证

取雷达参数和前文描述相同。目标距雷达为20km，其初始方位角为30°，运动方位角为60°，其初始运动速度为25m/s。令目标在运动过程中突然以－4m/s2的加速度进行减速，减速3s后目标以13m/s的速度运动直到跟踪结束(200s)。令目标减速起始时刻分别为t1=10s(情形1)，t2=60s(情形2)，t3=100s(情形3)。比较不同情形下由本文提出的滤波方法与衰减记忆滤波器的滤波性能比较。

图7为500次Monte Carlo试验后x、y方向上雷达探测目标位置以及滤波位置与目标真实位置的偏差随迭代步数累积的变化。

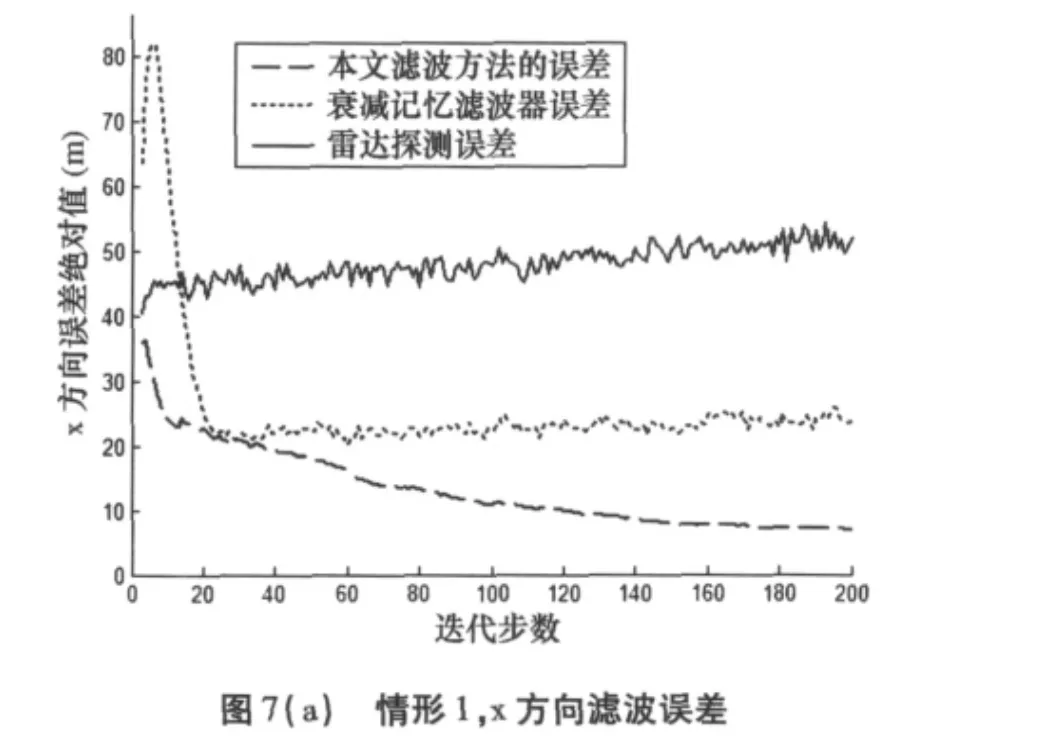
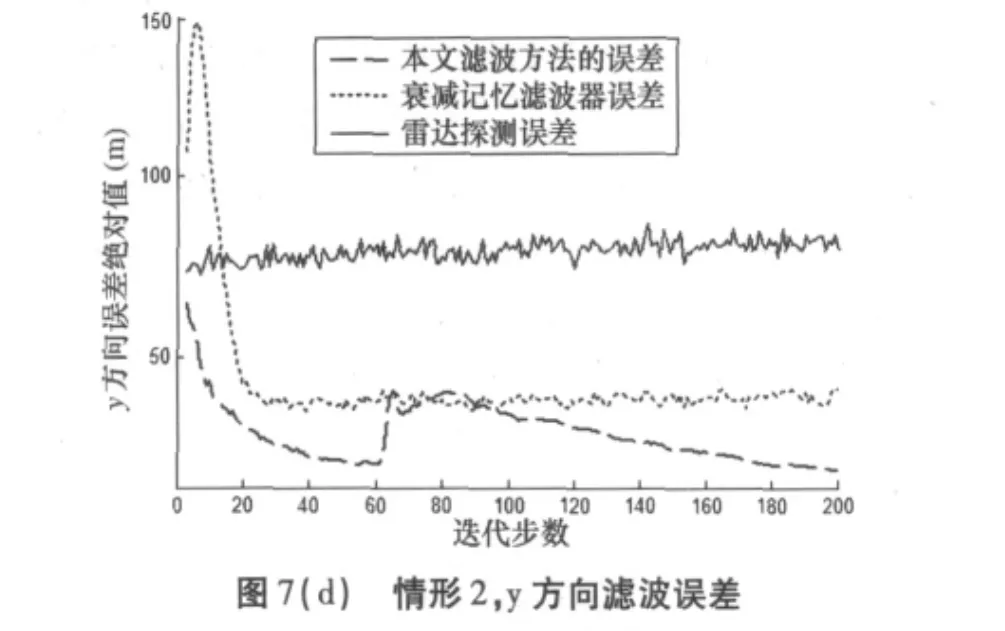
由图7a～7b可以看出，若目标加/减速发生在跟踪初期，则运动状态的变化对α-β滤波器的影响不大。由图7c～7f可以看出，若目标加/减速发生在跟踪稳定阶段利用本文滤波方法能兼顾衰减记忆滤波器的稳定性和α-β滤波器的高精度。该滤波方法能使跟踪精度在目标稳定运动的过程中得到持续的改善;当目标突发机动后，滤波误差会有一个增大过程，当误差达到或略高于衰减记忆滤波器滤波误差后(试验发现若能更为及时的判决目标瞬时机动，则该误差能进一步减小到接近甚至略低于衰减记忆滤波器滤波误差的水平)将继续随迭代步数的累积而减小，得到比衰减记忆滤波器更高的滤波精度。

4 结论

根据机载雷达对地目标跟踪的特点，本文提出结合利用α-β滤波器和衰减记忆滤波器的滤波算法。通过仿真验证了该算法能兼顾滤波器跟踪精度和滤波稳定性。该算法在判决目标突发生机动后以衰减记忆滤波器的滤波结果修正α-β滤波器的输出，易于工程实现。另外若能找到更好的目标瞬时机动判决依据，则该算法能得到更好的滤波效果。

［1］Bassem R.Mahafza.Radar System Analysis and Design Using MATLAB，Second Edition［M］. USA: Taylor ＆ Francis Group LLC，2005.

［2］何子述，夏威.现代数字信号处理及其应用［M］.北京:清华大学出版社，2009.

［3］孟真，于进勇，阎跃鹏.基于并行卡尔曼滤波的递推最小二乘测频算法［J］.微电子学与计算机，2011，28(3):1 －5.

［4］何友，修建娟，张晶炜等.雷达数据处理及应用(第二版)［M］.北京:电子工业出版社，2009.

［5］方青，梅晓春，张育平.用于机动目标跟踪的Kalman滤波器的设计［J］.雷达科学与技术，2006，4(1):50 －55.