合作空间目标双基地ISAR图像畸变分析及校正方法

尚朝轩,韩 宁,董 健,张大伟

(1.军械工程学院雷达工程教研室,石家庄050003;2.北京跟踪与通信研究所,北京100094)

1 引 言

双基地逆合成孔径雷达(Inverse Synthetic Aperture Radar,ISAR)因具有良好的“四抗性能”,以及对目标成像时不受目标运动方向限制等特点,成为雷达成像领域的一个重要研究方向[1-4]。昆士兰大学的J.Palmer系统地研究了伪多基地ISAR(Emulated Multistatic ISAR)成像技术[5,6],并进行实验验证,得到了一定分辨率的二维图像。挪威防御技术研究院研究的“搭乘雷达系统”得到了较清晰的民航客机双基地ISAR图像[7]。国内对双基地ISAR的研究主要集中在基本成像原理以及越距离单元徙动补偿等方面[8,9]。

双基地ISAR成像时,二维ISAR像会产生畸变,导致二维ISAR像与原目标散射点模型相差较大。针对此问题,北京理工大学的高梅国等人从成像平面的角度出发,分别采用基于双基地SAR成像平面分析和基于旋转矢量分析的方法对双基地ISAR成像平面进行研究,得出了双基地ISAR成像距离轴与方位轴不正交会造成图像畸变的结论[10]。但该文献分析过程较繁琐,对图像畸变的理解从复杂的运动矢量确定与计算出发,在实际应用时未为简易,不便于工程实现。

本文以平稳运行的合作空间目标为研究对象,从空间目标双基地ISAR的回波模型出发,研究了双基地ISAR图像的畸变机理,结合先验可知的空间目标精轨数据,对成像期间的双基地角进行估计,并提出了基于畸变角估计的图像畸变校正方法,最后通过仿真实验对本文方法的有效性进行了验证。

2 空间目标双基地ISAR回波模型

图1所示为运动目标双基地ISAR成像的几何关系。

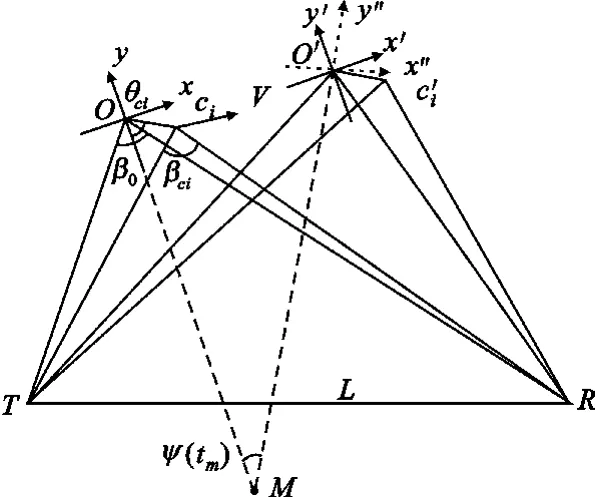
图1 双基地ISAR成像几何关系Fig.1 Bistatic ISAR imaging geometry

图1中,L为双基地雷达基线,T为发射站,R为接收站;y轴是开始观测时目标的双基地角平分线方向;β0是目标双基地角,βci是目标上散射点ci的双基地角,近似认为 β0≈βci;点 O是相位中心;θci是散射点ci的位置矢量Oci与y轴负方向的夹角;V为目标运动速度;ψ(tm)为成像期间双基地角平分线的转动角度。假定双基地雷达理想同步,且雷达发射LFM信号,则经中频直接采样数字下变频后,散射点ci的基带回波可用式(1)表示如下

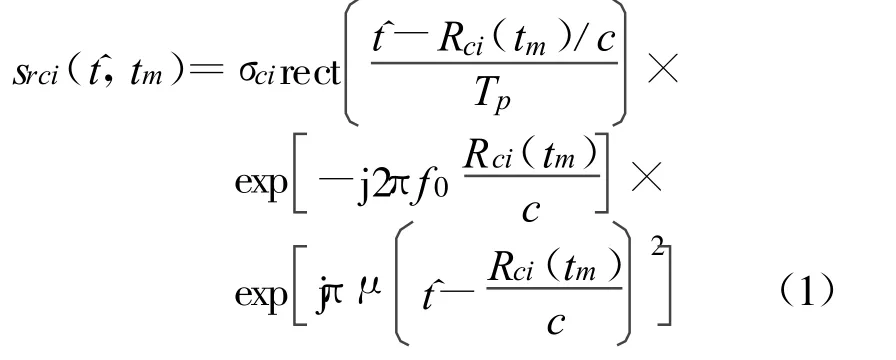
式中, t是快时间;tm是慢时间;f0是载频;c是真空中光速;μ是调频斜率;Tp是脉冲宽度;σci为第 i个距离单元内散射点ci的非后向散射强度。

理论分析得出,双基地ISAR成像过程中,平稳空间目标上散射点的距离变化可按式(2)表示如下[11]:

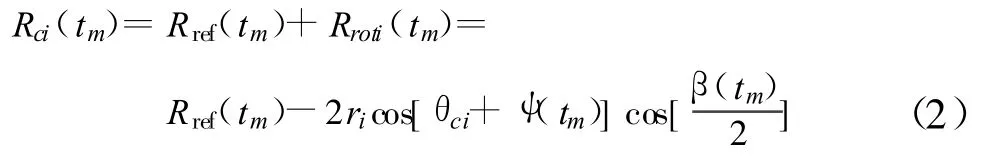
其中,tm=mT(m=0,1,2,…)是慢时间;β(tm)是目标成像期间随慢时间变化的目标双基地角;Rref(tm)是成像过程中目标相位中心到收发双站的距离历程,即目标运动的平动项;Rroti(tm)是散射点ci的转动距离项。

从式(2)可以看出,双基地ISAR成像中,目标散射点的距离变化依然包括平动分量Rref(tm)和转动分量Rroti(tm)两部分,因此,双基地ISAR同样可经距离压缩、包络对齐、初相校正、方位压缩等几步,完成对目标的二维成像[11]。

3 双基地ISAR图像畸变机理

单基地 ISAR成像中,距离-多普勒(Range-Doppler,RD)算法是最简便,物理意义最明确的一种算法。其基本思想是通过回波信号的脉冲压缩,完成散射点的距离分辨,然后通过慢时间上的多普勒分析,实现散射点的方位分辨。该成像原理同样适用于双基地ISAR,且已有的双基地ISAR成像研究中,大都基于RD算法[1-3],故本文同样使用RD算法进行二维成像。散射点的平动距离项Rref(tm)不影响ISAR成像所需的转动多普勒信息,因此后文研究假设Rref(tm)已完全补偿。

当视角变化较小时,复杂模型可视为由一定分布的众多散射点所组成[12],为比较方便地研究图像畸变机理,本文假设平稳空间目标的散射点模型如图2所示。

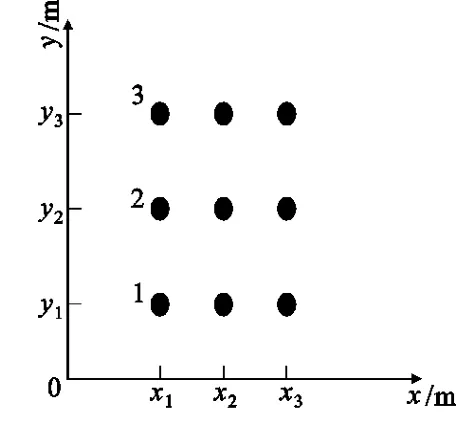
图2 目标的散射点模型Fig.2 Target scatter model

其中,横轴为几何方位轴,即图1中的x轴;纵轴为几何距离轴,即图1中的y轴。在研究图像畸变机理的过程中,只需散射点的相对位置关系即可,因此图2并未给出各散射点坐标的绝对数值,只给出其相对数值。

双基地雷达多普勒频移fB定义为波长λ归一化的散射信号总路径长度随时间的变化率[13],因此由转动距离项Rroti(tm)造成的转动多普勒为

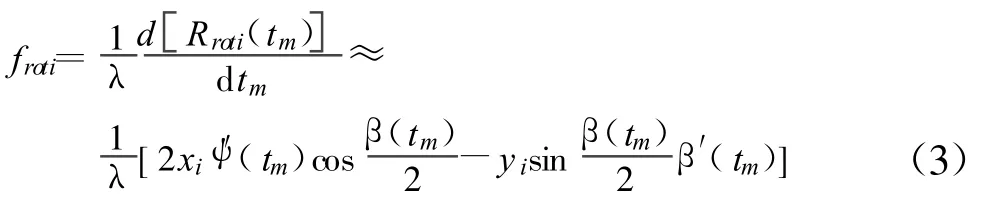
ISAR成像以目标的几何距离为纵坐标,以多普勒为横坐标。在成像坐标平面中,设纵坐标用y′表示,横坐标用 fB表示,且假定图2中散射点1、2、3的坐标分别为(x1,y1)、(x1,y2)、(x1,y3),则依据式(3)可得

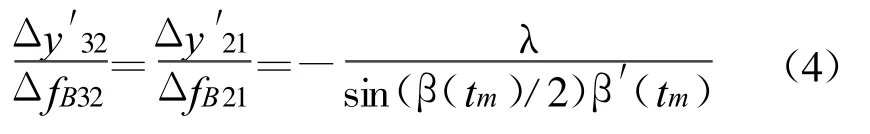
式中,λ为载波波长;Δy′32、Δy′21分别表示成像平面坐标中散射点3与散射点2,以及散射点2与散射点1之间的纵坐标之差;ΔfB32、ΔfB21分别表示散射点3与散射点2,以及散射点2与散射点1之间的转动多普勒之差。

分析(4)式可得以下结论,目标散射点模型中有相同几何方位轴的散射点,在目标成像平面中依然处于同一直线上,只是直线与横轴的夹角由初始的90°变为图像畸变角θ,从而造成了ISAR二维像的畸变,且畸变角θ可以按下式进行估计:

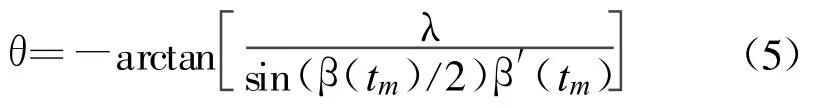
分析(3)式还可看出,若 β′(tm)=0,即成像期间双基地角不发生变化,则目标散射点模型中有相同几何方位轴的散射点,在目标成像平面中依然具有相同的多普勒,与横轴的夹角依然是90°,即二维ISAR像不会发生畸变。综合以上分析可以看出,成像期间变化的双基地角最终造成了二维ISAR像的畸变。当图像发生畸变时,其畸变效果可用图3表示。与图2相同,图3只给出了各散射点的相对多普勒及相对几何距离。观察图3可以看出,图像畸变后目标散射点的几何距离没有发生变化,仅仅是横向位置进行了偏移,图3中的 θ即为畸变角。文献[10]将与图3中虚线正交的轴定义为成像方位轴,得出了成像距离轴即图3中的 y′轴与成像方位轴不正交会导致图像畸变的结论。本文不引入该方位轴的定义,直接从ISAR二维像中散射点的投影轴即y′和fB解释了畸变机理,这样更加直观,便于理解。

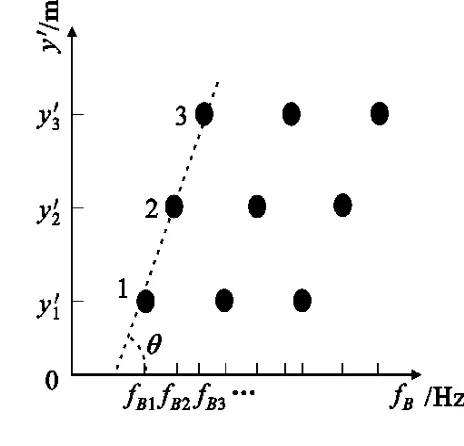
图3 目标成像平面Fig.3 Target imaging plane

4 图像畸变的校正方法

本文第2节分析得出,经RD算法成像后,目标二维ISAR像会产生畸变。畸变效果可看成是目标散射点在保持纵向距离不变的条件下,横向上受到均匀“挤压”,最终造成了图像的畸变。因此,若能估计出图像畸变角θ,然后对图像进行反向畸变补偿,即可实现图像的畸变校正。

4.1 图像畸变角估计方法

分析式(5)可以看出,在载波波长已知的前提下,若能估计出目标的双基地角β(tm),即可按照式(5)对图像畸变角 θ进行估计。对于合作的空间目标,可通过高精度的测控设备获得其精轨数据,然后通过解双基地三角形获得目标的双基地角 β(tm)。实际成像过程中,双基地角随慢时间变化,因此只能利用双基地角的平均值 β(tm)对畸变角 θ进行估计。此时,畸变角θ可按式(6)进行估计:

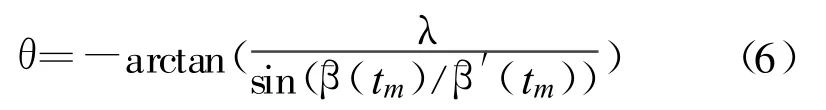
4.2 图像畸变校正的基本步骤

假设雷达每个PRT采样M点数据,每行为一个距离单元,共有N个PRT数据,则图像数据的大小为M×N。并设第一行数据代表的距离最小,以该行图像数据作为校正基准,第行数据的多普勒畸变单元数Δfm可表示为

式中,Δyr表示快时间域相邻采样点代表的距离;Δfm>0代表图像向右畸变,Δfm<0代表图像向左畸变。

利用双基地角的平均值 β(tm)对畸变角θ进行估计,将式(6)代入式(7)化简可得

当Δfm不是整数时,对其进行四舍五入处理得到最接近的整数值。得到Δfm的估计值后,对图像矩阵进行反向移位即可实现畸变校正。图像畸变校正的基本步骤如下:

Step1:依据空间目标的精轨数据,估算成像期间目标的双基地角平均值 β(tm);

Step2:利用式(8)估计第m行数据的多普勒畸变单元数Δfm;

Step3:对第m行数据进行反向畸变补偿,即将该行对应的横向多普勒数据统一减去;

Step4:重复2～3步,直至完成整幅图像的畸变校正。

因第1行数据已有横向多普勒的畸变,但上述方法将其作为校正基准,故校正后的二维像横向多普勒与散射点的真实多普勒会不一致。但该方法可准确恢复散射点间的相对位置,仍得到正确的目标外形结构,因此用其进行畸变校正是可行的。

5 仿真实验

仿真过程中,假定双基地雷达满足时间、空间和频率的三大同步要求,发射站雷达发射LFM信号,载波频率为10 GHz,脉冲宽度为50 μ s,脉冲重复频率50 Hz,信号带宽为200 MHz,采样频率250 MHz,基线长度为650 km。

使用STK软件生成国际空间站的轨道数据,利用其估计成像期间的平均双基地角并对回波进行平动补偿,目标散射点模型及仿真场景如图4所示。图4(a)为目标散射点模型,图4(b)为双基地ISAR成像的仿真场景。

使用RD算法进行二维成像,利用方位向分辨率约束成像时间,使成像期间不发生越距离单元徙动和越多普勒单元徙动,并利用3.2节的畸变校正方法对二维ISAR像进行畸变校正,校正前后的目标二维像如图5所示。图5(a)为校正前的二维像,图5(b)为校正后的二维像。

图4 目标散射点模型及仿真场景Fig.4 Scatter model and simulation scene

图5 畸变校正前后的二维像对比Fig.5 ISAR before and after correction

将图5与图4进行对比可以看出,畸变校正前双基地ISAR的二维像发生畸变,已不能正确反映目标的结构信息,利用本文方法对其进行校正后,虽然横向多普勒已不再是目标散射点对应的正确多普勒数值,但二维ISAR像恢复了原始目标的正确形状,验证了本文方法的有效性。

6 结 论

本文以平稳运行的空间目标为研究对象,从散射点回波模型出发,研究了双基地ISAR二维像的畸变机理,提出了首先利用精轨数据进行图像畸变角估计,然后利用其估计畸变单元数,最后对图像进行畸变校正的方法,算法简单且较易工程实现,理论分析和仿真实验验证了算法的有效性。

[1]Martorella M.Bistatic Isar Image Formation in Presence of Bistatic Angle Changes and Phase Synchronisation Errors[C]//Proceedings of 2008 7th European Conference on Synthetic Aperture Radar.Friedrichshafen,Germany:IEEE,2008:105-108.

[2]Martorella M,Palmer J,Berizzi F,et al.Advances in Bistatic Inverse Synthetic Aperture Radar[C]//Proceedings of 2009 International RadarConference Surveillance fora Safer World.Bordeaux:IEEE,2009:1-6.

[3]Victor C Chen,Andre des Rosiers,Lipps Ron.Bi-Static Isar Range-Doppler Imaging and Resolution Analysis[C]//Proceedings of IEEE Radar Conference.Pasadena,CA:IEEE,2009:1-5.

[4]朱仁飞,张群,罗迎,等.含旋转部件目标双基地ISAR微动特征提取及成像研究[J].电子与信息学报,2010(10):2359-2364.ZHU Ren-fei,ZHANG Qun,LUO Ying,et al.Study onMicro-motion Feature Extraction and Imaging of T arget with Rotating Parts in Bistatic ISAR[J].Journal of Electronics&InformationTechnology,2010,(10):2359-2364.(in Chinese)

[5]Palmer J,H omer J,Longstaff I.D,et al.Isar Imaging Using an Emulated Multistatic Radar System[J].IEEE Transactions on Aerospace and Electronic Systems,2005,41(4):1464-1472.

[6]Palmer J,Homer J,Mojarrabi B.Improving on the Monostatic Radar Cross Section of Targets by Employing Sea Clutter to Emulate a Bistatic Radar[C]//IEEE InternationalGeoscience and Remote Sensing Symposium,2003,1:324-326.

[7]Overrein O,Olsen K E,Sornes P K,et al.Geometrical and Signal Processing Aspects Using a Bistatic Hitchhiking Radar System[C]//Proceedings of 2005 IEEE International Radar Conference.Washington DC:IEEE,2005:332-336.

[8]高昭昭.高分辨ISAR成像新技术研究[D].西安:西安电子科技大学,2009.GAO Zhao-zhao.New T echnologies of High ResolutionISAR Imaging[D].Xi′an:Xidian University,2009.(in Chinese)

[9]朱小鹏,张群,朱仁飞,等.双站ISAR越距离单元徙动分析与校正算法[J].系统工程与电子技术,2010,32(9):1828-1832.ZHU Xiao-peng,ZHANG Qun,ZHU Ren-fei,et al.Study on Correction Algorithm of Migration through Resolution Cell in Bistatic-ISAR.[J].Systems Engineering and Electronics,2010,32(9):1828-1832.(in Chinese)

[10]董健,尚朝轩,高梅国,等.双基地ISAR成像平面研究及回波模型修正[J].电子与信息学报,2010,32(8):1855-1862.DONG Jian,SHANG Chao-xuan,GAO Mei-guo,et al.The Image Plane Analysis and Echo Model Amendment of Bistatic ISAR[J].Journal of Electronics&Information Technology,2010,32(8):1855-1862.(in Chinese)

[11]董健,尚朝轩,高梅国,等.空间目标双基地ISAR成像的速度补偿研究[J].中国电子科学研究院学报,2010(1):78-85.DONG Jian,SHANG Chao-xuan,GAO Mei-guo,et al.Research on Bistatic ISAR Speed Compensation of Space Target[J].Journal of China Academy of Electronic and Information Technology,2010(1):78-85.(in Chinese)

[12]保铮,邢孟道,王彤.雷达成像技术[M].北京:电子工业出版社,2005.BAO Zheng,XING Meng-dao,WANG Tong.Radar Imaging Technology[M].Beijing:Publishing House of Electronics Industry,2005.(in Chinese)

[13]杨振起,张永顺,骆永军.双(多)基地雷达系统[M].北京:国防工业出版社,1998.YANG Zhen-qi,ZHANG Yong-shun,LUO Yong-jun.Bistatic(Multistatic)Radar Systems[M].Beijing:National Defense Industrial Press,1998.(in Chinese)