高速主轴回转误差动态测试与分析

靳 岚 燕昭阳 谢黎明 苟卫东 施东兴

(①兰州理工大学机电工程学院，甘肃兰州 730050;②青海一机数控机床有限责任公司，青海西宁 810018)

随着高速、高精密机床的发展，在机械加工过程中，高速主轴的回转误差已经成为影响工件加工精度的关键因素，它直接影响到被加工零件的几何形状精度和表面粗糙度［1］。

主轴回转误差是指主轴的瞬间回转轴线相对于平均轴线(处于瞬间回转轴线的平均位置处)的位移。主轴回转误差可以分解为3种基本形式:纯轴向窜动、纯径向跳动和纯角度摆动。其中后两者总称为主轴径向回转误差，它是影响加工误差的主要因素［2］。

1 测试系统原理

三点测量法是利用3个传感器按照一定的角度垂直布置在被测标准件的同一截面上对主轴进行误差测量，此方法需要对3个传感器安装固定，安装调试繁琐，成本高，而且装夹精度要求高。因此根据高速主轴实验的情况，该系统选择两点法进行测量，安装简单，能快速方便地测得主轴误差运动，并有效地分离主轴回转误差中的主轴偏心误差，直观地显示运动误差图像。

图1为测试系统图，采用双向测试法设计系统，即在主轴轴端安装高精度的检测棒，把2个电涡流传感器(非接触的电容传感器)以90°夹角垂直地安装在检测棒同一截面圆上，以拾取x、y向两路信号。在空载运行状态下，利用电涡流传感器与检测棒(模拟刀具安装在电主轴上)之间的位移变化来检测主轴轴向振动。电涡流传感器输出信号到LMS TEST.LAB信号采集中，经过信号处理后输入计算机，并在计算机中实时显示图像。

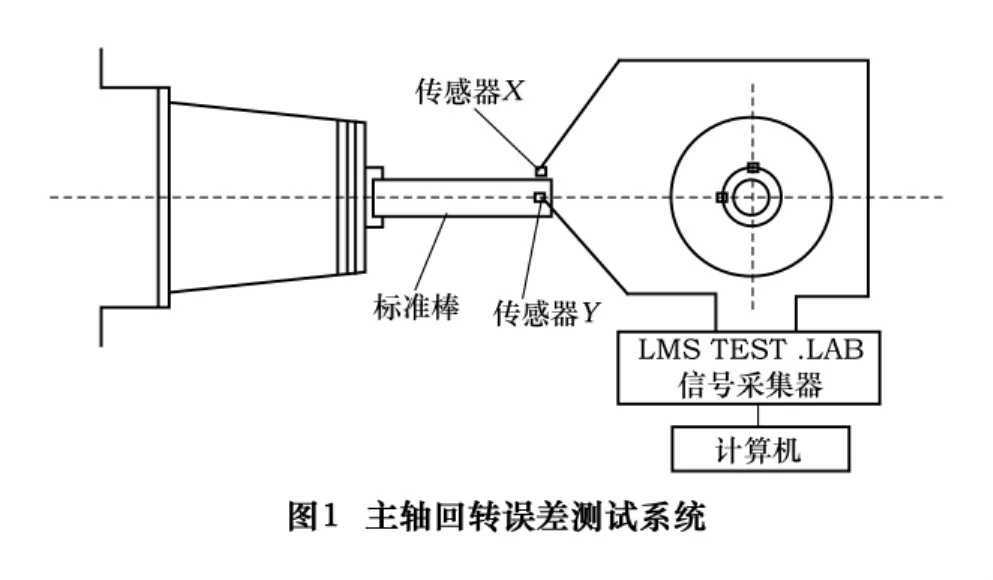
本次实验采用高速主轴进行测试，相对一般主轴随着其转速的提升，尤其12 000 r/min以上时轴承温度可能会迅速升高，会引起主轴的弯曲变形，造成测试的不准确。因此本实验在测试过程中还对高速主轴进行了温度的监控，以排除温升对测试结果的影响。应用温度传感器采集前后轴承的温度，传入计算机并实时显示温度数据。经过实时的温度监控主轴温升小于30°，在规定范围之内，因此此次实验温升对主轴的影响可以忽略。

2 测试误差分析

用电涡流传感器(非接触位移传感器)进行主轴回转误差测量时，由于实际的主轴回转轴心是不可见的，不能直接对其测量，而只能通过对外装的主轴上的标准件(标准球或标准棒)的测量来间接测得主轴轴心运动，因而这样的测量方法不可避免会混入标准件外轮廓的形状误差和安装误差。对于具有高回转精度的精密主轴，混入的形状误差或安装误差的影响是不容忽视的，它们甚至会掩盖掉微小的主轴回转误差，所以需要寻找有效的误差分离方法将其从采集的数据中准确地分离出去。

3 误差分离数学模型

目前，对主轴回转误差的测量国内外普遍采用电容或电感涡流传感器对安装在主轴上的标准球进行单点或多点测量，测量信号中一般都含有主轴回转误差信号、标准棒(或标准球)安装偏心信号和标准棒(标准球)截面形状误差信号。需要从测量信号中分离出误差信号，通常使用频域法，对测量信号作正反两次傅立叶变换，运用滤波技术对测量信号进行误差分离。在测量不同转速的机床回转误差时，需要不断改变滤波器的类型和参数，才能从中找到最适合的滤波器，用一般的编程语言更改数字滤波器时需要编写复杂的程序，难度和工作量较大，而且程序的通用性不好。鉴于滤波分离的一些缺点，本文提出了一种分离偏心误差的数学模型，可以有效地把偏心误差从检测信号中分离出来。

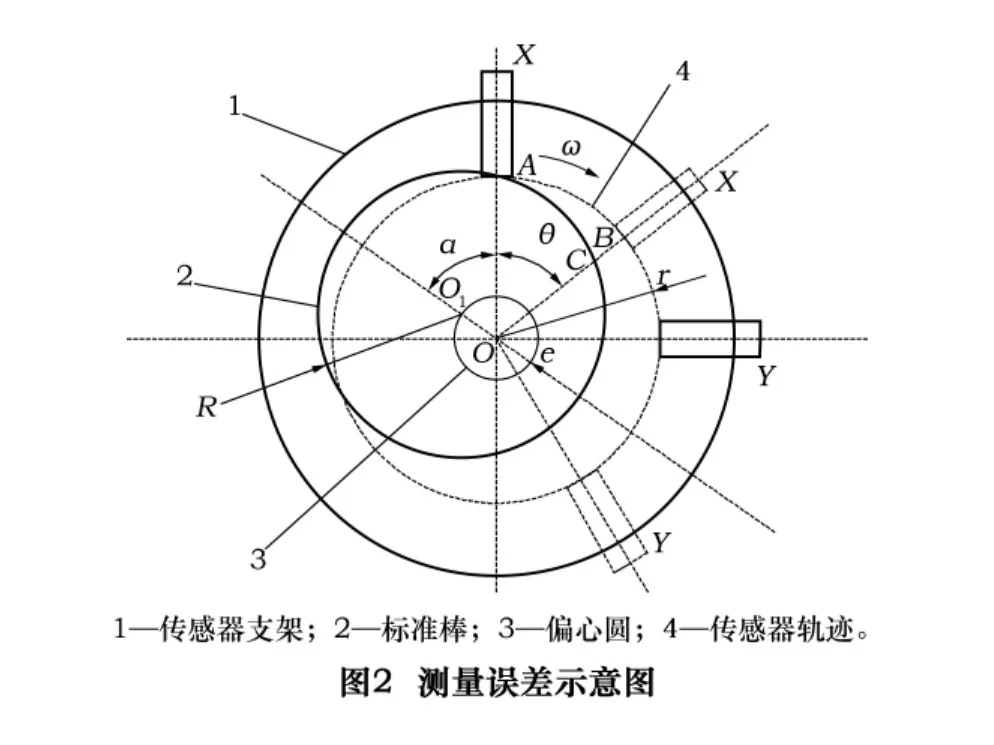
传感器测量到的主轴回转误差在敏感方向的信号可通过如图2所示原理图进行推导。

图中圆1为支架，与主轴同心;圆2为标准棒;圆3为假设标准棒不动，传感器x、y相对标准棒反向运动轨迹;圆4为以O为圆心以偏心量e为半径的圆，O为主轴回转中心，O1为标准棒轴心，R为标准棒半径，r为传感器运动轨迹圆心，α为传感器x的初相位，θ为传感器旋转角度，A为传感器初始位置，B为传感器旋转θ角后的位置，BC为由于偏心量引入的误差。设传感器测量信号为x(t)，主轴回转转速为ω，主轴回转误差x向分量为δx，偏心量引入误差为Δex，标准球截面形状误差为Δ，那么传感器检测到的信号可表示为

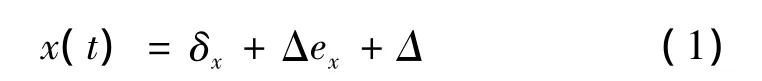
式(1)由于选择高精度标准棒(误差＜0.02 μm)，因此标准棒截面形状误差Δ可以忽略不计。式(1)可以简化为

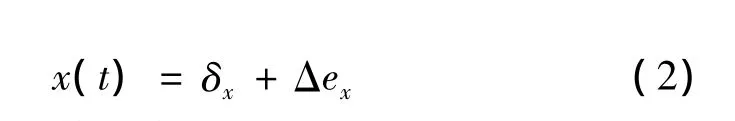
由图2测量误差示意图可知:

主轴回转中心到标准棒圆面上的距离Lx为

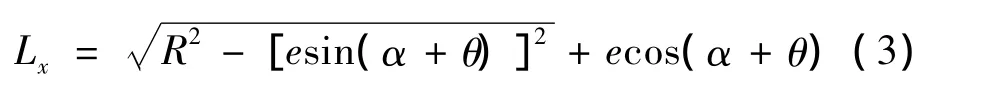
传感器回转轨迹圆半径r为

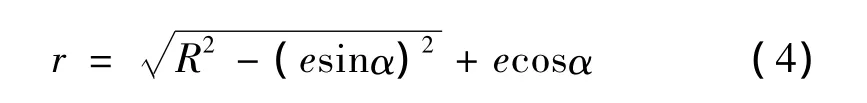
安装偏心误差Δex为

由于y向与x向相位相差90°，因此

应用上述误差分离数学模型，得到主轴回转误差δx、δy，消除了安装偏心误差。这种消除偏心的方法是得到确切的安装偏心误差信号，从而在检测信号中消除，不仅消除了安装偏心误差带来的一次谐波、二次谐波，而且也消除了高次谐波所带来的影响。

4 实验分析

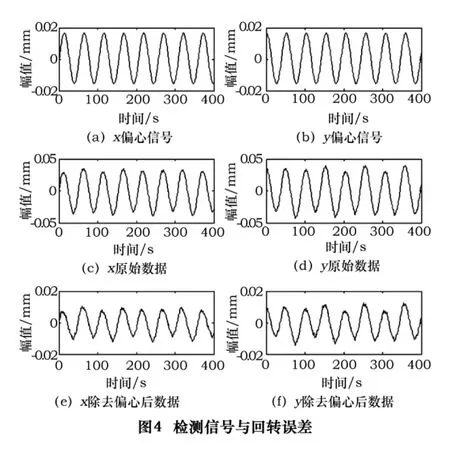
按图1所示检测系统测量高速主轴在15 000 r/min下回转误差运动，实际测量位移变化曲线如图3所示。

图3a、3b分别为采集信号偏心误差信号Δex、Δey，其相位相差90°;图3c、3d分别为采集信号x(t)、y(t)，其相位相差90°;图3e、3f分别为采集信号除去偏心误差后的主轴回转误差 δx、δy(δx=x(t)－ Δex，δy=y(t)－Δey)。

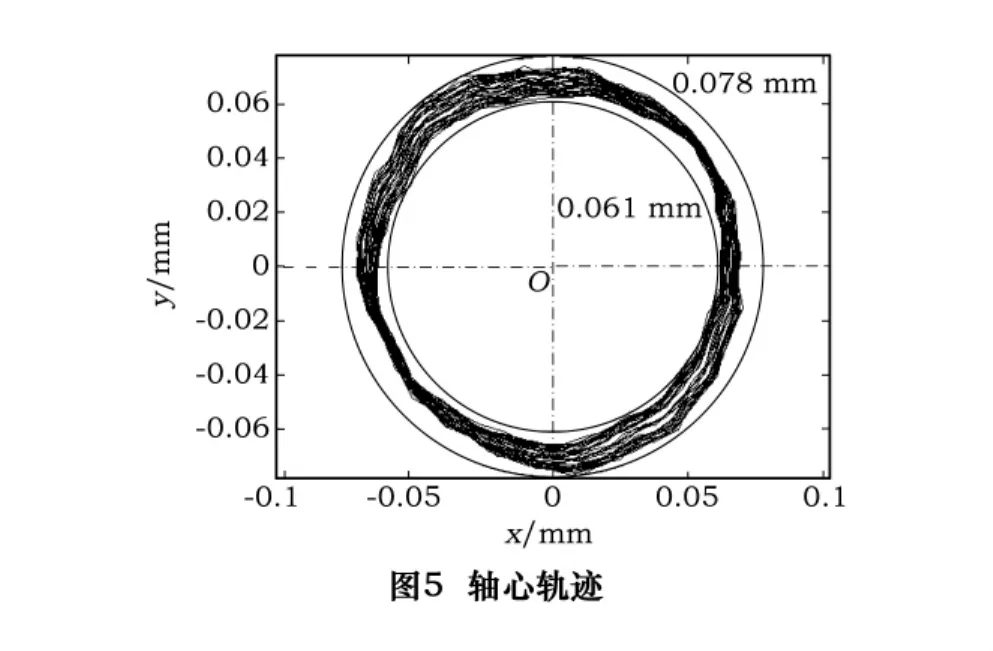
将采集来的信号经过偏心处理采用圆图像方式记录，就是在测得的数据基础上叠加一个基圆，也就是加上一个直流分量，形成一个偏离真圆的误差运动圆图，并用拟合最小二乘圆法对误差运动进行评定如图4所示。

采用最小二乘圆法来计算回转误差［4－5］。

(1)求出最小二乘圆的圆心坐标(a，b)

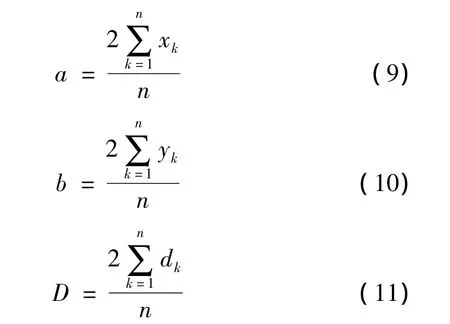
式中:xk和yk为实际轮廓上各等分点的横坐标和纵坐标;n为被测圆的等分数，n值越大结果越精确;dk为点(xk，yk)到坐标原点的径向距离。

(2)求轮廓上各点到最小二乘圆圆心的距离

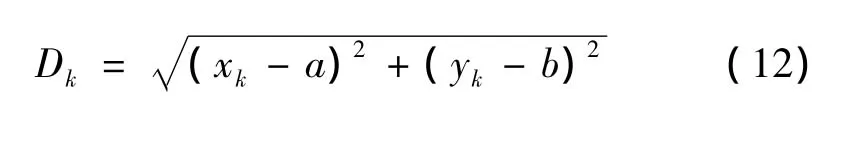
式中:Dk为被测点到最小二乘圆圆心的距离。

(3)计算回转误差

式中:f为主轴回转误差。

从图4可以看出在主轴某一方向上的回转误差较大，说明轴承在这个方向上刚度较差，在加工的时候，他会把回转误差一比一地映射到加工工件上的几何形状误差和尺寸误差中。

5 结语

本文介绍了主轴回转误差的测量理论及测试方法。根据测试数据进行分析和偏心误差处理，获取工作状态下的主轴回转信息，对标准棒安装误差进行分析，并建立偏心误差数学模型去除采集信号中的偏心误差，从而可以高精度地获得主轴回转误差信息。实验验证，文中研究的测试系统能准确地测量主轴的回转精度，建立的偏心误差数学模型能有效地分离检测信号中的偏心误差，这对提高加工机床精度、保证机械产品质量具有现实意义。

［1］王翔.计算机辅助回转精度测量系统的研制［J］.机械与电子，2006(7).

［2］伍良生，杨勇，周大帅.机床主轴径向回转误差的测量与研究［J］.机械设计与制造，2009(1).

［3］黄长征，李圣怡.超精密车床主轴回转误差运动的动态测试［J］.航空精密制造技术，2002，38(4).

［4］王少蘅.高速精密主轴回转误差在线动态测试技术研究［D］.广州:广东工业大学，2006.

［5］费业泰.误差理论与数据处理［M］.北京:机械工业出版社，1991:119－201.