基于改进自适应遗传算法求解机床制造企业立体仓库堆垛机路径优化问题
2012-09-28周耿烈冯无恙胡赤兵
周耿烈 冯无恙 胡赤兵②
(①兰州理工大学机电工程学院,甘肃兰州 730050;②兰州理工大学数字制造技术与应用省部共建教育部重点实验室,甘肃兰州 730050)
成本、质量、生产率和产量、交货期是衡量机床制造企业生产能力和巿场竞争能力的4个要素[1]。机床零部件加工后要经过严格的检验进入全自动化立体仓库存放,再由立体仓库送至装配作业线进行部件装配,装配完成的部件经过严格的部装检验后进入立体仓库。立体仓库根据生产需要将零部件送到装配作业线进行总装。如何在保证机床质量的前提下降低生产成本包括物流成本,同时提高机床的生产率和产量,并依据客户要求按时交货是机床制造企业关注的重点。
立体仓库是现代物流系统中迅速发展的一个重要组成部分,在制造自动化中也占有非常重要的地位。在机床制造企业建立立体仓库及其信息管理系统其目的不仅是为了进行毛坯、半成品、成品、工装夹具等的自动存储和自动检索,更是密切配合企业的产销计划与物料需求计划。由于机床不同零部件的制造周期不一样,为保证产品成套既要按期交货,又要尽可能减少由于产品积压所导致的生产管理混乱现象,立体仓库管理系统是现代化立体仓库不可或缺的一部分。
随着自动化立体仓库在生产线当中的应用,形成了以自动化立体仓库为核心的物流配送系统,从采购、外协到货、检验入库、毛坯出库、加工、零件入库、装配及产品生成,都要与自动化立体仓库协调。
自动化立体仓库要求作业迅速、准确、稳定等特点。其作业周期由出入库台的时间、货物登记时间和堆垛机在仓库存取货物时间等组成。由于现代化立体仓库规模越来越大,其高度达50多m,长度也达150 m,所以在整个物流周期中堆垛机的行驶时间占到整个仓库作业周期的50%。如果堆垛机调度不当或选用效率较低的调度模式,会严重影响堆垛机的工作效率,进而影响整个仓库的作业效率。所以选择一种较为合理的拣选路径是提高堆垛机作业效率的方法。
在对堆垛机的路径进行分析时,国内外学者已对仓库中的货位存取优化,单复合作业的优化、堆垛机拣选作业的优化及输送系统的调度优化进行了广泛的研究。自动化立体仓库堆垛机路径优化的算法研究,包括蚁群算法、模拟退火算法、启发式算法、禁忌搜索算法[2-5]及遗传算法等。其中遗传算法能够得出较好的全局最优解,具有搜索速度快、精度高等优点。
1 自动化立体仓库模型的建立
假设堆垛机的工作空间(立体仓库)用二维平面图形来表示。堆垛机执行一次任务时所不能通过的货格的位置已知。用尺寸相同的栅格对立体仓库进行划分。若某一栅格内不含任何障碍物,则称此栅格为自由栅格;反之,称之为障碍栅格[6]。如图1所示。

2 改进的自适应遗传算法
遗传算法是一种借鉴生物界自然选择和自然选择机制的随机化搜索算法,对于用传统搜索方法难以解决的复杂和非线性问题具有良好的适应性。但还有很多不足,如早熟收敛、易陷入局部最优和收敛速度慢等。本文采用改进的自适应遗传算法对堆垛机的工作环境进行建模,找到堆垛机路径优化的最佳路径。
当今改进遗传算法的措施主要集中于对交叉概率和遗传概率的选择与确定上,因为它们会影响遗传算法的收敛性和搜索速度。针对不同的优化目标需要反复试验来确定交叉概率和遗传概率,而传统的遗传算法采用的是固定数值来代替交叉概率和遗传概率,这样很难找到最佳优化目标。
自适应遗传算法(AGA)[7]是由 Srinivas提出来的,它的基本思想是交叉概率和变异概率能够随着适应度的变化而变化。当种群各个体适应度处于趋于一致或者局部最优时,使交叉概率和变异概率增加,从而避免陷入局部最优,继而引发早熟现象;当群体各个体适应度比较分散时,使交叉概率和变异概率减少,从而不易破坏优良个体,以利于优良个体保存下来。同时,对适应度高于群体平均适应度的个体选择较小的交叉概率和变异概率,使得个体保存下来;那些低于群体平均适应度的个体,选择较大的交叉概率和变异概率,一方面将一部分差的个体淘汰,另一方面增加新个体[8]。在自适应遗传算法中,交叉概率pc和变异概率pm按如下公式进行调整:

式中:fmax为种群的最大适应度;favg为种群的平均适应度;f′为参与交叉的2个个体中较大的个体的适应度;f为变异个体的适应度。
AGA算法是有缺陷的。从公式中可以看出,当个体适应度越接近于最大适应度(fmax-f′≈0)时,交叉概率和变异概率越小,到接近为零,这种调整方法在群体优化后期较为合适,因为在后期,要将优良个体保存下来,即为全局最优解。但是在进化初期不利,因为在进化初期群体中的较优个体几乎处于一种不发生变化的状态,而此时的优良个体不一定是全局最优解,增加了进化走向局部最优解的可能性,就是所谓的早熟现象。
任子武等人在AGA的基础上,提出了一种改进的自适应遗传算法(IAGA)。它除了有AGA的一系列优点之外,还弥补了AGA的缺陷。为了保证每一代的优良个体不被破坏,采取了精英保留策略:如果下一代的最佳个体适应度小于当前种群的最佳个体适应度,那么将当前种群的最佳个体或者多个个体直接复制到下一代,从而不会被当代种群的交叉和变异等遗传操作破坏[8]。IAGA 公式如下:

式中:pc1、pc2分别为交叉概率的最大值和最小值;pm1、pm2分别为变异概率的最大值和最小值。
在IAGA算法中,根据公式,个体的交叉概率和变异概率应根据个体的适应度在平均适应度和最大适应度之间进行线性变换。如果种群中存在较大规模的适应度接近平均适应度的个体,它的交叉概率最大,几乎为pc1和pm1,若个体适应度接近于最大适应度,那么它的交叉概率和变异概率很小,为pc2和pm2,即IAGA的自适应交叉概率和变异概率曲线非常陡峭,导致一部分个体只能拥有较低的交叉概率和变异概率,使进化停滞不前,造成局部收敛[9]。
本文所要提出的新的改进自适应遗传算法是根据种群的大小、适应值的分布情况、自适应变化整个种群的交叉概率和变异概率,使它们的变化曲线为一个从振荡而逐渐稳定的形势。设计进化前期具有较大的交叉概率和变异概率,以增强搜索能力,在进化后期采取相对较低的交叉概率和变异概率,以确定最佳个体。本文将采用正弦形式的自适应遗传算法(SAGA),其公式如下:
图2和图3为两个公式所表示的图像,均为正弦式图像,从而保证了交叉概率和变异概率呈一种稳定式变化,而不会出现过度陡峭曲线,因为-1<sina<1,它可以弱化由于适应度接近平均适应度或者接近最大适应度而造成的交叉概率和变异概率的过大或者过小,也克服了由于种群停滞不前而陷入局部最优的现象。


3 路径规划方法
3.1 编码
采用序号法。基本顺序是从左到右,从下到上。将立体仓库分为若干个空格,从立体仓库的左下角的第一个格开始,给每一个空格一个序号N,依次延续,这样序号N与立体仓库的每一个空格一一对应。
我们将堆垛机在立体仓库的一条运动路径称之为一个个体,在这里假设堆垛机由起始位置A经过这一条路径最终到达终点位置B,那么这条路径可以表示为一个个体。采用序号法,则表示为以下所示:(0,1,11,13,22,32,34,45,56,66,77,87,88,99),我们从中可以看出,每条路径采用序号法具有编码长度短、简明、直观的优点。
3.2 初始种群
在选取初始种群时,为了使堆垛机行驶的路径最短,在起始点与终点连线的两侧分布初始点,把这些点称之为过渡点。把上一点与下一点的选取作为一个周期,每个周期选择与当前堆垛机的位置距离最小的点作为当前时刻的规划子目标点。如果子目标点不是障碍物,则此点为最佳点;若是障碍物,则选取此点周围的过渡点为候选点。这样规划出的路径都是围绕起点和终点连线的,确保点的分布不会太分散,这样可以规划出最短路径。
3.3 个体适应度函数
在这里选取如下所示的个体适应度函数:


3.4 遗传算子设计
3.4.1 选择算子
采用轮盘赌选择和精英保留相结合的方法,是个体按照与适应度成正比例的概率向下一代群体繁殖。
3.4.2 交叉算子
采用部分匹配交叉法:先随机产生两个 ,定义这两点间的区域为匹配区域,并用位置操作交换两个父代的匹配区域。如:交叉点为3、6父代A872 130 9546父代B983 567 1420,先交换130与567,得出来的两个过渡代为A′872 567 9546父代B′983 130 1420,对于A′、B′中的匹配区域以外出现的数码重复,要依据匹配区域内的位置逐一进行交换。即5和1进行交换,6和3进行交换,7和0进行交换。这样经过交叉之后,子代A为 8025679143,同理,子代B为9861305427。
3.4.3 变异算子
其变异算子采用逆转变异算子,方法如下:在个体中随机挑选两个逆转点,再将两个逆转点间的基因反序插入原位置。如个体A:987654321,在第4号位与第6号位采用逆转变异算子。新生成的个体为987456321。
3.4.4 平滑算子
堆垛机采用导轨式行走装置,所以在行驶到转弯路径时要求拐弯处角度大,从而引出路径平滑度问题。平滑度是指路径段之间偏转角度的大小。如果转角过小,则会增加堆垛机行走过程的复杂性,其消耗时间过长,甚至会导致堆垛机因转角过小而无法通过。
平滑算子是在路径段之间的转角处两端添加两个或多个节点,替代原有的节点,使得路径转角处更加平滑,使堆垛机顺利通过此处。
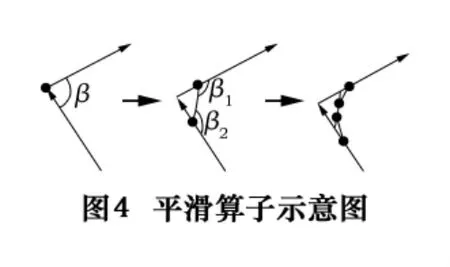
设堆垛机的转弯最小角度为α,如图4所示.当判断出两个相连路径的拐角偏转角度β<α时,则分别在拐角附近的两端可行域附近随机选取两个新节点,这样就形成了两个拐角处,这时分别判断两个拐角处的偏转角度是否大于α,若大于则替代原节点,否则在两节点处的两端可行域再选择两个新节点,直至符合要求。
4 仿真分析
采用Matlab遗传算法工具箱对此进行仿真测试。设种群规模为40,每个种群的长度为20,交叉概率pc=0.9,变异概率为pm=0.01,然后利用SAGA对每一代的交叉概率和变异概率进行计算。在Matlab窗口中输入Gatool,打开、进入遗传算法工具箱。之前必须将适应度函数写成M文件。
决定遗传算法的一个重要性能是种群的多样性。个体间的距离越大,则多样性越高;反之,个体间的距离越小,则多样性越小。
设置“initial range”为[0;1],其显示图形如图 5所示。

图5的上图中较为密集的点为每一代的最佳适应度值(Fitness value),而在密集点周围的较为分散的点为每一代的平均适应度值,它可以很好地用来衡量种群的多样性。对于初始范围的设置,由于多样性太小,算法进展很小。设置“initial range”为[0;100],运行算法,如图6所示。

这次算法进展较快。但是,由于个体之间的平均距离较大,最佳个体原理最优解。
设置“initial range”为[0;20],运行算法,如图7所示。
这次由于多样性比较适合,所以算法得到的结果比前两次都好。
图7上图为遗传算法过程中群体中每一代个体最佳适应度随进化代数(Generation)的变化情况。可以看出,改进后的遗传算法收敛较快,进化到约34代就已经接近搜索到了全局最优解。在早期各代中,当个体离理想值较远时,最佳值会迅速得到改进;在后来各代中,种群越接近最佳点,最佳值改进的越慢,正好顺应了SAGA的要求,图7的下图很好地解释了这些情况。它为每一代中(每一代中会产生一定数量的点,各点所对应的适应度值不一样)各点之间的平均距离。当变异数减小时,个体之间的平均距离也减小,逐渐向零靠近。可以看出,当进化代数在40代之前,个体之间的平均距离较大,这符合了SAGA的要求,即在进化前期,不要一味地将适应度值差的个体淘汰掉,而是要通过交叉和变异将个体改良,这样既增加了种群的多样性,又不至于产生局部最优化,导致引起的早期收敛现象。而从第40代往后,个体之间的平均距离减小,这意味着代与代之间的差异性较小,全局最优解基本产生了。

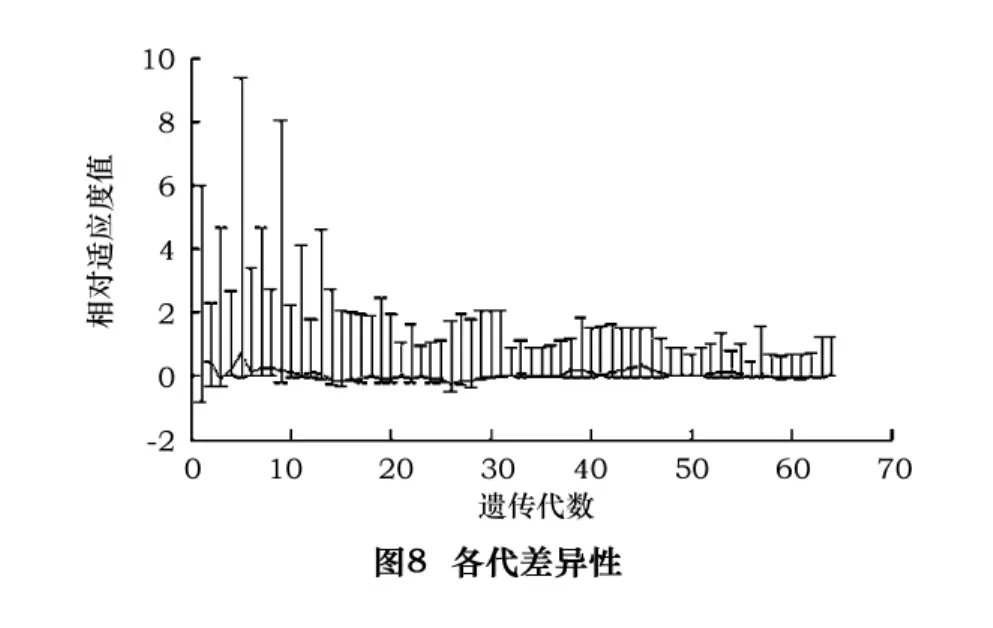
通过图8所示可以清晰地看到自适应算法在算完100代之后,这其中的每一代的具体情况,图8中每一条的垂直线表示每一代中各点适应度值由最小到最大的范围,在图形的下方所看到的一条曲折的线是遗传算法在完成进化100代之后平均适应度值演化趋势。40代之前,每一代的种群之间适应度差异较大,所以线条长度较长;而40代之后,差异性迅速缩小并趋于稳定化,所以线条长度较短。与此相对应的是平均适应度也由较大范围的变化逐渐缩小并最终趋于稳定。这说明当变异数减小时,适应度值的范围也减小,这些图形显示减小变异数,也就减小了子辈的多样性,加快了收敛速度,这说明全局最优解接近产生了。
5 结语
本文提出改进的自适应遗传算法(SAGA),不仅克服了传统遗传算法的早熟和收敛速度慢问题,而且大幅度提高遗传算法的工作效率。此方法应用于堆垛机的路径规划,可提高堆垛机的路径规划质量和工作效率。通过Matlab遗传算法工具箱的仿真,进一步验证了此方法的有效性和可行性。通过自动化立体仓库技术和软件技术实现对物料的智能化管理,减少产品积压,提高机床制造企业在激烈市场中的竞争能力。
[1]马千里.机床制造企业立体仓库信息管理系统研究[J].控制管理,2008,4(3):5 -7.
[2]华红艳,张丹.基于蚁群算法的自动化立体仓库路径优化[J].计算机技术与自动化,2010,29(1):51 -54.
[3]杜宗宗,刘国栋.基于混合模拟退火算法求解TSP问题[J].计算机工程与应用,2010,46(29):40 -42.
[4]陆文,郭延涛,李文杰.基于改进遗传算法的车间调度问题求解[J].现代制造工程,2010(10):35-37.
[5]王清校,郎茂祥,彭永昭,等.基于禁忌搜索算法的货物运输路径和方式选择问题研究[J].物流技术,2010(12):96-98.
[6]孙树栋,曲彦宾.遗传算法在机器人路径规划中的应用研究[J].西北工业大学学报,1998,16(1):79 -83.
[7]SRINVAS M,PATNAIK L M.Adaptive probabilities of crossover and mutation in genetic algorithms[J].IEEE Trans on Systems,Man and Cybernetics,1992,24(6):656 -667.
[8]张京钊,江涛.改进的自适应遗传算法[J].计算机工程与应用,2010,46(11):53 -55.
[9]任子武,伞冶.自适应遗传算法的改进及在系统辨识中应用研究[J].系统仿真学报,2006,18(1):41 -46.
[10]张国强,彭晓明.自适应遗传算法的改进与应用[J].舰船电子工程,2010(1):83-84.
