基于独立的Gaussian与Beta有限维混合模型的聚类算法

2012-09-25刘洋

大庆师范学院学报 2012年3期

刘洋

(大庆师范学院数学科学学院，黑龙江大庆 163712)

基于模型的聚类算法受到生物医药学界，统计学界，金融界，计算机等领域的高度重视。本文针对独立的Gaussian与Beta有限维混合模型建立一种新的聚类方法，BGMMn聚类算法。此算法更适合独立的Gaussian与Beta有限维混合数据，特别是Gaussian分布数据容易聚类的有限维混合数据，有较高的聚类数目估计的准确度。

1 混合模型

观测指标或样本数据集X={X1,X2,X3,…Xn}分为G个类，假设数据以权重πk(k=1,2,…G)来自每一个类。令X=(YT,ZT)T，其中Y为Beta分布有限维观测数据，Z为Gaussian分布有限维观测数据，并且假设Y与Z有相同的类的结构形式，Yi与Zi相互独立，i=1,2，…n。则

θ1k=(αk1,αk2，…αkp1;βk1,βk2，…βkp1)为参数。

记θk=(θ1k,θ2k),θ=(θ1,θ2…θG)，则观测数据的联合概率模型为

引入数据集X的分类标签Hi=(hi1,hi2,…hiG)T, 若数据Xi来自第k个类，则hik=1；否则hik=0，其中k=1,2，…G，i=1,2，…n。于是观测数据联合概率模型的log-似然函数为

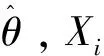
把分类标签H看成缺失向量，可以利用EM算法[1]的E步得到完全数据集的log-似然函数。

2 BGMMn聚类算法

2.1 BGMMn算法流程

1)给出分布中参数π,μ,σ的初值：

2)利用EM算法[1]估计Gaussian分布参数μ,Σ，得到

其中v=1,2，…p2;k=1,2，…G。

3)更新分类指标τik

4)重复2)与3)直到收敛为止。

5)利用第3)步收敛时τik的取值，根据分类准则：若{w|τiw=maxw{τiw}}，则数据Xi属于第w类，得出有限维混合数据X的初始分类。

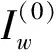
9)循环6)，7)，8)步骤，直到算法收敛为止。

2.2 模型选择

利用模型选择标准AIC[2]，BIC[3]，AIC3[2]，ICL[4]各自确定的聚类数目选择最优的模型选择标准。在相同的背景框架下，对BGMMn聚类算法分别应用上述四种模型选择标准进行数据模拟，比较得到的正确聚类个数的次数，选择最优的模型选择标准。模拟结果AIC，BIC，AIC3， ICL得到的正确聚类个数的次数分别为22，6，19，6。于是BGMMn聚类算法应用AIC作为给出最优聚类个数的模型选择标准。

2.3 算法评价的优良标准

为了客观的评价算法的优良，研究有限维混合数据的真实聚类与算法得到的聚类二者之间的所有可能的联系[5]。为了估计BGMMn聚类算法估计的准确度，对随机产生的数据集进行模拟，比较有限维混合数据的真实的聚类数目与算法得到的聚类数目，若二者的聚类数目一致，则记为1，否则记为0，模拟结束后，对记录结果进行累加，其和记为N，于是算法聚类数目估计的准确度可以通过式子“N×模拟次数的倒数”进行计算。

3 模拟结果

为检验BGMMn聚类算法的优势，比较了BGMMn聚类算法与BGMMs聚类算法[5]，BGMMa聚类算法[5]，BGMMh聚类算法[5]对聚类数目估计的准确度。模拟数据集见表1，对数据集模拟10000次后4种聚类算法对聚类数目估计的准确度见表2。

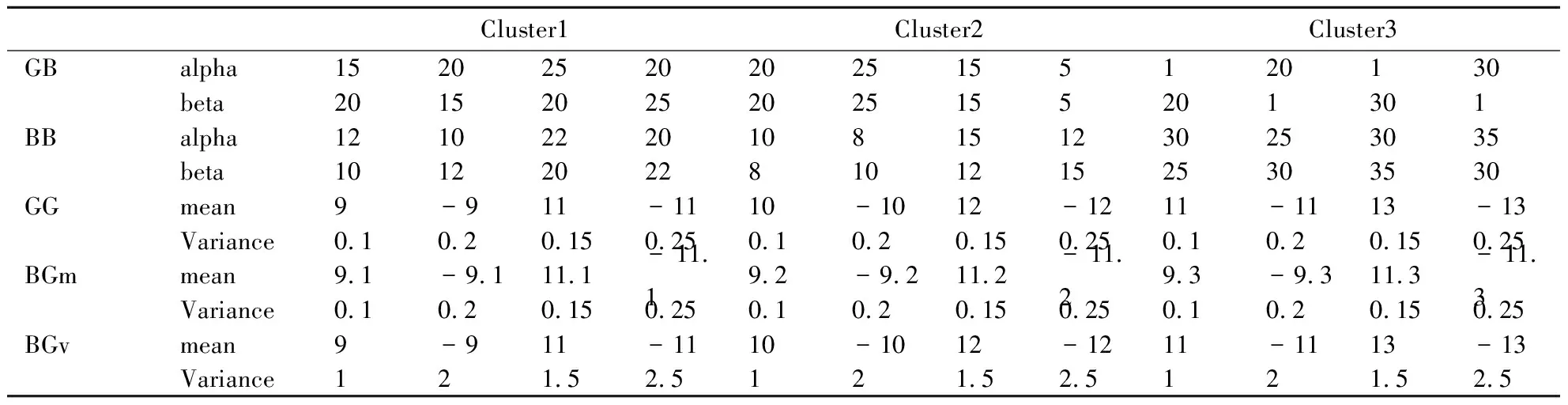
表1 模拟的数据集

注：GB为容易聚类的Beta分布数据，BB为不容易聚类的Beta分布数据，GG为容易聚类的Gaussian分布数据，BGm为均值接近时不容易聚类的Gaussian分布数据，BGv表示方差很大时不容易聚类的Gaussian分布数据。

表2 聚类数目预测的准确度

4 结语

通过对独立的Gaussian与Beta有限维混合模型的聚类算法的研究，提出BGMMn聚类算法。在相同的背景下，通过模拟4种聚类算法的聚类数目估计的准确度，表明该算法的优势，也指出Gaussian分布数据容易聚类时该聚类算法较其他三种聚类算法更为有效。

[参考文献]

[1] Little R J A, Rubin D B.缺失数据统计分析[M].孙山泽,译.北京:中国统计出版社,2004：143-152.

[2] Biernacki C, Govaert G.Choosing models in model-based cluslering and discriminant analysis[J].Journal of statcstical Computarion and simulation,1999,64: 49-71.

[3] Pan W.Incorproating gene functions as priors in model-based clustering of microarray geneexpression data[J].Bioinformatics, 2006,22 (7): 795-801.

[4] Ji Y, Wu C, Liu P, et al. Applications of beta-mixture models in bioinformatics[J].Bioinformatics,2005,21 (9): 2118-2122.

[5] Xiao Feng D, Timo E, Olli Y H, et al. A joint finite mixture model for clustering genes from independent Gaussian and beta distributed data[J].BMC Bioinformatics, 2009,10 :165.