随机延迟微分方程随机θ方法的几乎处处指数稳定

张 玲

(大庆师范学院 数学科学学院, 黑龙江 大庆 163712 )

1 引言与预备

在这篇文章不做特别的说明，我们令|x|是欧几里得范数，令(Ω,F,P)是完备的概率空间，并具有满足通常条件的代数流{Ft}t≥0。

引理1[2]：对于t≥0，令A(t),U(t)是两个Ft可测的增过程，并且A(0)=U(0)=0 a.s.，令M(t)是实值的局部鞅，并且M(0)=0a.s.，令ζ是非负F0可测的随机变量。假设X(t)是非负并且对于t≥0有X(t)=ζ+A(t)-U(t)+M(t)。如果limt→∞A(t) <∞a.s.，那么对于几乎所有的ω∈Ω,有

limt→∞X(t) <∞和limt→∞U(t) <∞

也就是，X(t)和U(t)都收敛到有限的随机变量。

引理2[3]：对于i=1,2，…，令{Ai},{Ui}是两个非负的随机变量序列，使得Ai和Ui是Fi-1可测的并且A0=U0=0a.s.，令Mi是实值的局部鞅并且M(0)=0a.s. ，令ζ是非负F0可测的随机变量。假设{Xi} 是一个非负半鞅并且有分解

Xi=ζ+Ai-Ui+Mi

如果limi→∞Ai<∞a.s.，那么对于几乎所有ω∈Ω, limi→∞Xi<∞ 和limi→∞Ui<∞,也就是，Xi和Ui都收敛到有限的随机变量。

我们考虑n维的随机延迟微分方程

(1)

其中f,g:C(Rn×Rn;Rn)，并且w(t)是一个维纳过程。为了研究稳定性，我们假设f(0,0)=g(0,0)=0。下面给出研究问题的条件局部Lipchitz条件：

(2)

下面是本篇文章的主要结果，首先给出解析解的稳定性结果，之后给出方程(1)的随机θ方法，并且应用半鞅收敛定理来证明这个方法得到的数值解是几乎处处指数稳定的。

2 解析解和数值解的稳定性

我们首先给出方程(1)的随机θ方法

(3)

(4)

定义2[5]称离散的方程(3)的数值解xk是几乎处处指数稳定的，如果存在一个常数η>0，对于有界随机变量ξ(kh),k=-m,-m+1，…0，使得

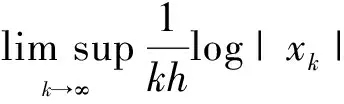
(5)

下面的定理给出了随机微分方程(1)解析解的几乎处处稳定。

定理1：在假设3满足的情况下，假设有四个非负常数λ1,λ2,λ3,λ4，对于所有的x,y∈Rn和t≥0，使得

2xTf(x,0)≤-λ1|x|2

(6)

|f(x,y)-f(x,0)|≤λ2|y|

(7)

|g(x,y)|2≤λ3|x|+λ4|y|

(8)

成立，如果

λ1>2λ2+λ3+λ4

(9)

其中γ>0是下面式子唯一的根

λ1-λ2-λ3-γ=(λ2+λ4)eγτ

下面让我们讨论随机延迟微分方程随机θ方法数值解的稳定性，假设f满足线性增长条件，也就是，存在一个K>0，使得

|f(x,y)|2≤K(|x|2+|y|2)

(10)

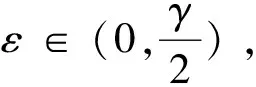
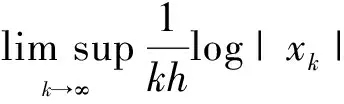
(11)

证明：由(3)得

(12)

对于任意的整数C>1，我们有

C(k+1)h|xk+1|2-Ckh|xk|2=C(k+1)h(|xk+1|2-|xk|2)+(C(k+1)h-Ckh)|xk|2

(13)

把(12)代入(13)，并且由条件(6)-(10)我们得到

(14)

其中

我们把(14)不等式两侧进行求和得

(15)

因为

把上面三个式子代入(15)，当1-a2>0时，

其中

让我们先讨论下面这个函数

φ(C)=(a1+λ3h)Ch+a2+a4Cmh+(a3+λ4h)C(m+1)h

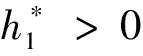
因此，对于任意的C≥1，我们得到φ'(C)>0。得到

φ(1)=-(λ1-2λ2-λ3-λ4-2Kh)h

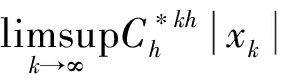
选择μ使得C=eμ并且1-C-h=1-e-μh。下面定义函数

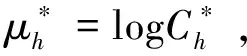
(16)

(17)

通过γ的定义，(16)和(17)得到

进一步有

3 结语

综上所述，本文给出了随机延迟微分方程解析解和数值解的几乎处处指数稳定，我们应用的是随机θ方法，证明的方法建立在连续和离散鞅收敛定理上，以往别人做的技巧是应用了切比雪夫不等式和大数定律，在这篇文章中主要应用鞅收敛定理，直接给出了随机延迟微分方程数值解的几乎处处指数稳定的性质，这为以后继续研究随机微分方程解析解和数值解的性质奠定了一定基础，并提供理论根据。

[参考文献]

[1] Mao, X. LaSalle-type theorems for stochastic differential delay equations[J]. J. Math. Anal. Appl.，1999,236(4)：350-369.

[2] Mao, X. The LaSalle-type theorems for stochastic differential equations[J]. Nonlinear Stud.，2000,7(2)： 307-328.

[3] Mao, X. A note on the LaSalle-type theorems for stochastic differential delay equations[J]. J. Math.Anal. Appl.，2002, 268(8)： 125-142.

[4] Mao, X. Numerical solutions of stochastic functional differential equations[J]. LMS J. Comput. Math.，2003,6(2)： 141-161.

[5] Mao, X. Exponential stability of equidistantEuler-Maruyama approximations of stochastic differential delay equations[J]. J. Comput. Appl. Math.，2007, 200(12)：297-316.

[6] Mao, X., Rassias, M.J. Khasminskii-type theorems for stochastic differential delay equations[J]. Stoch.Anal. Appl.，2005,23(5)：1045-1069.

[7] Pang, S., Deng, F., Mao, X. Almost sure and moment exponential stability of Euler-Maruyama discretizations for hybrid stochastic differential equations[J]. J. Comput. Appl. Math.，2008, 213(9)：127-141.

[8] 胡迪鹤.随机过程论基础、理论、应用[M].武汉：武汉大学出版社,2000:56-78.